Файл: Курсовая работа по дисциплине Математика Тема Математические методы и модели исследования операций.docx
Добавлен: 07.12.2023
Просмотров: 58
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
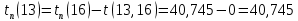
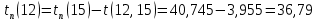
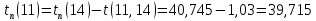
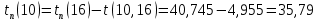
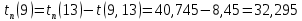
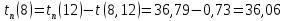
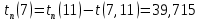
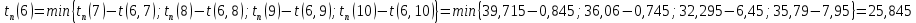
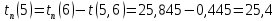
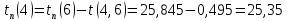
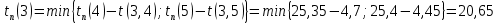
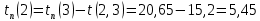
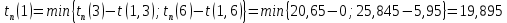
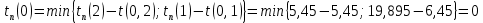
Полученные данные оформлю в виде таблицы 13.
Таблица 13 – Основные параметры событий
| Событие | Предшествующие работы | Время предшествующих работ | Ранний срок 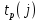 | Последующие работы | Время последующих работ | Поздний срок 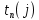 | Резервы R(j) |
| 0* | - | - | 0 | (0, 1) | 6,45 | 0 | 0 |
| (0, 2) | 5,45 | ||||||
| 1 | (0, 1) | 6,45 | 6,45 | (1, 3) | 0 | 19,895 | 13,445 |
| | | (1, 6) | 5,95 | ||||
| 2* | (0, 2) | 5,45 | 5,45 | (2, 3) | 15,2 | 5,45 | 0 |
| 3* | (1, 3) | 0 | 20,65 | (3, 4) | 4,7 | 20,65 | 0 |
| (2, 3) | 15,2 | (3, 5) | 4,45 | ||||
| | | (3, 6) | 3,95 | ||||
| 4* | (3, 4) | 4,7 | 25,35 | (4, 6) | 0,495 | 25,35 | 0 |
| 5 | (3, 5) | 4,45 | 25,1 | (5, 6) | 0,445 | 25,4 | 0,3 |
| 6* | (1, 6) | 5,95 | 25,845 | (6, 7) | 0,845 | 25,845 | 0 |
| (3, 6) | 3,95 | (6, 8) | 0,745 | ||||
| (4, 6) | 0,495 | (6, 9) | 6,45 | ||||
| (5, 6) | 0,445 | (6, 10) | 7,95 | ||||
| | | (6, 11) | 0,63 | ||||
| 7 | (6, 7) | 0,845 | 26,69 | (7, 11) | 0 | 39,715 | 13,025 |
| 8 | (6, 8) | 0,745 | 26,59 | (8, 12) | 0,73 | 36,06 | 9,47 |
| 9* | (6, 9) | 6,45 | 32,295 | (9, 13) | 6,45 | 32,295 | 0 |
| 10 | (6, 10) | 7,95 | 33,795 | (10, 16) | 4,955 | 35,79 | 1,995 |
| 11 | (6, 11) | 0,63 | 26,69 | (11, 14) | 1,03 | 39,715 | 13,025 |
| (7, 11) | 0 | | | ||||
| 12 | (8, 12) | 0,73 | 27,32 | (12, 15) | 3,955 | 36,79 | 9,47 |
| 13* | (9, 13) | 8,45 | 40,745 | (13, 16) | 0 | 40,745 | 0 |
| 14 | (11, 14) | 1,03 | 27,72 | (14, 16) | 0 | 40,745 | 13,025 |
| 15 | (12, 15) | 3,955 | 31,275 | (15, 16) | 0 | 40,745 | 9,47 |
| 16* | (10, 16) | | 40,745 | (16, 17) | 0,68 | 40,745 | 0 |
| (13, 16) | 0 | | | ||||
| (14, 16) | 0 | | | ||||
| (15, 16) | 0 | | | ||||
| 17* | (16, 17) | 0,68 | 41,425 | (17, 18) | 4,15 | 41,425 | 0 |
| 18* | (17, 18) | 4,15 | 45,575 | (18, 19) | 4,15 | 45,575 | 0 |
| 19* | (18, 19) | 4,15 | 49,725 | (19, 20) | 12,95 | 49,725 | 0 |
| 20* | (19, 20) | 12,95 | 62,675 | - | - | 62,675 | 0 |
Резервы времени событий, через которые проходит критический путь, равны нулю, значит критический путь:
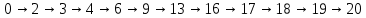
Выделю критический путь на сетевом графике.
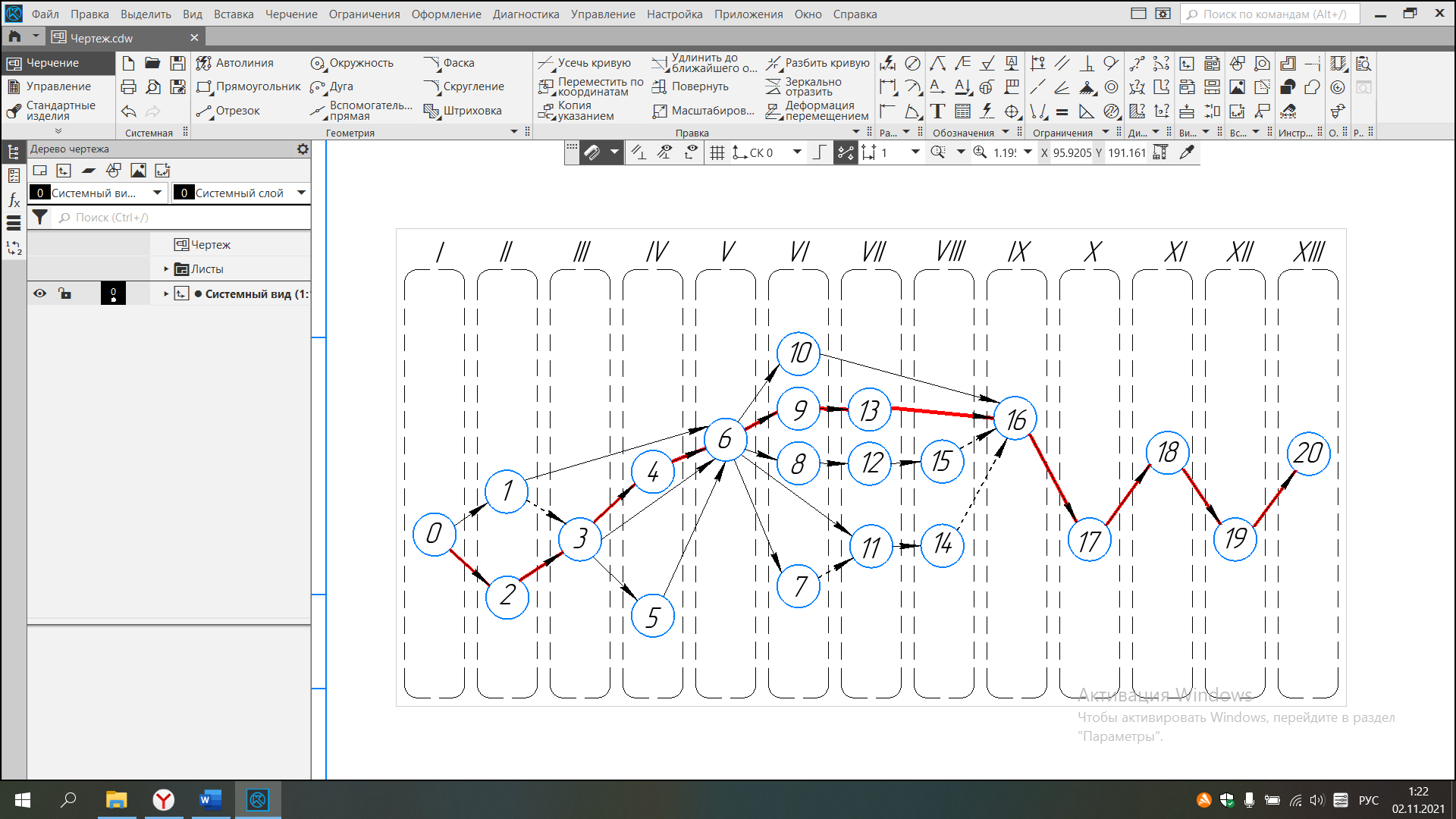
Рисунок 1 – Сетевой график
Вычислю основные параметры работ, а именно
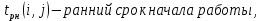
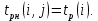
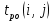 – ранний срок окончания работы,
– ранний срок окончания работы,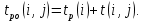
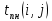 – поздний срок начала работы
– поздний срок начала работы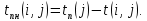
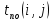 – поздний срок окончания работы, резервы и независимые резервы.
– поздний срок окончания работы, резервы и независимые резервы. 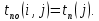
Полученные результаты занесу в таблицу 14.
Полный резерв времени Rп показывает, насколько можно увеличить время выполнения данной работы при условии, что срок выполнения всего комплекса работ не изменится. Находится согласно формуле:
Rп(i,j)=tпо(i,j) - tро(i,j)= tп(j) - tр(i) - t(i,j).
Независимый резерв времени
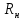 показывает резерв времени, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние. Определяется по формуле:
показывает резерв времени, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние. Определяется по формуле: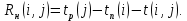
Таблица 14 – Основные параметры работ
| № | Работы | tож | Сроки | Резервы | ||||
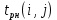 | 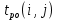 | 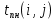 | 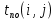 | 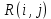 | 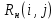 | |||
| 1 | (0, 1) | 6,45 | 0 | 6,45 | 13,445 | 19,895 | 13,445 | 0 |
| 2 | (0, 2) | 5,45 | 0 | 5,45 | 0 | 5,45 | 0 | 0 |
| 3 | (1, 3) | 0 | 6,45 | 6,45 | 20,65 | 20,65 | 14,2 | 0 |
| 4 | (1, 6) | 5,95 | 6,45 | 12,4 | 19,895 | 25,845 | 13,445 | -0,755 |
| 5 | (2, 3) | 15,2 | 5,45 | 20,65 | 5,45 | 20,65 | 0 | 0 |
| 6 | (3, 4) | 4,7 | 20,65 | 25,35 | 20,65 | 25,35 | 0 | 0 |
| 7 | (3, 5) | 4,45 | 20,65 | 25,1 | 20,95 | 25,4 | 0,3 | 0 |
| 8 | (3, 6) | 3,95 | 20,65 | 24,6 | 21,895 | 25,845 | 1,245 | 1,245 |
| 9 | (4, 6) | 0,495 | 25,35 | 25,845 | 25,35 | 25,845 | 0 | 0 |
| 10 | (5, 6) | 0,445 | 25,1 | 25,545 | 25,4 | 25,845 | 0,3 | 0 |
| 11 | (6, 7) | 0,845 | 25,845 | 26,69 | 38,87 | 39,715 | 13,025 | 0 |
| 12 | (6, 11) | 0,63 | 25,845 | 26,475 | 39,085 | 39,715 | 13,24 | 0,215 |
| 13 | (6, 8) | 0,745 | 25,845 | 26,59 | 35,315 | 36,06 | 9,47 | 0 |
| 14 | (6, 9) | 6,45 | 25,845 | 32,295 | 25,845 | 32,295 | 0 | 0 |
| 15 | (6, 10) | 7,95 | 25,845 | 33,795 | 27,84 | 35,79 | 1,995 | 0 |
| 16 | (7, 11) | 0 | 26,69 | 26,69 | 39,715 | 39,715 | 13,025 | -13,025 |
| 17 | (11, 14) | 1,03 | 26,69 | 27,72 | 39,715 | 40,745 | 13,025 | -13,025 |
| 18 | (8, 12) | 0,73 | 26,59 | 27,32 | 36,06 | 36,79 | 9,47 | -9,47 |
| 19 | (9, 13) | 8,45 | 32,295 | 40,745 | 32,295 | 40,745 | 0 | 0 |
| 20 | (10, 16) | 4,955 | 33,795 | 38,75 | 35,79 | 40,745 | 1,995 | 0 |
| 21 | (12, 15) | 3,955 | 27,32 | 31,275 | 36,79 | 40,745 | 9,47 | -9,47 |
| 22 | (14, 16) | 0 | 27,72 | 27,72 | 40,745 | 40,745 | 13,025 | 0 |
| 23 | (13, 16) | 0 | 40,745 | 40,745 | 40,745 | 40,745 | 0 | 0 |
| 24 | (15, 16) | 0 | 31,275 | 31,275 | 40,745 | 40,745 | 9,47 | 0 |
| 25 | (16, 17) | 0,68 | 40,745 | 41,425 | 40,745 | 41,425 | 0 | 0 |
| 26 | (17, 18) | 4,15 | 41,425 | 45,575 | 41,425 | 45,575 | 0 | 0 |
| 27 | (18, 19) | 4,15 | 45,575 | 49,725 | 45,575 | 49,725 | 0 | 0 |
| 28 | (19, 20) | 12,95 | 49,725 | 62,675 | 49,725 | 62,675 | 0 | 0 |
По сетевому графику определю критические дуги и соответствующие им некритические дуги сетевого плана. Вычислю резервы и коэффициенты напряжённости для каждой пары дуг.
Вводится понятие коэффициента напряженности некритической дуги:
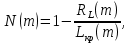
где
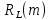 – резерв времени;
– резерв времени; 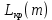 – длина критической дуги.
– длина критической дуги.
Таблица 15 – Критические и некритические дуги сетевого плана
| Некритическая дуга m | Соответствующая критическая дуга | Длина некритической дуги L(m) | Длина соответствующей критической дуги 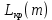 | Резерв времени 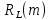 | Коэффициент напряженности 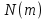 |
| 0-1-3 | 0-2-3 | 6,45 | 20,65 | 14,2 | 0,32 |
| 0-1-6 | 0-2-3-4-6 | 12,4 | 25,845 | 13,445 | 0,49 |
| 3-6 | 3-4-6 | 3,95 | 5,195 | 1,245 | 0,77 |
| 3-5-6 | 3-4-6 | 4,895 | 5,195 | 0,3 | 0,95 |
| 6-10-16 | 6-9-13-16 | 12,905 | 14,9 | 1,995 | 0,85 |
| 6-8-12-15-16 | 6-9-13-16 | 5,43 | 14,9 | 9,47 | 0,36 |
| 6-11-14-16 | 6-9-13-16 | 1,66 | 14,9 | 13,24 | 0,11 |
| 6-7-11-14-16 | 6-9-13-16 | 1,875 | 14,9 | 13,025 | 0,12 |
Коэффициент напряженности:
(0 – 0,4) - слабая напряженность
[0,4; 0,7) - средняя напряженность
[0,7; 0,9) - высокая напряженность
[0,9; 1) - крайне высокая напряженность
3.3 Оптимизация сетевого плана по критерию «стоимость»
Построю модель линейного программирования для решения данной задачи:
-
Введём переменные.
Пусть Ts(i, j) и Tf(i, j) - время (сроки), дни, начала и окончания работы (i,j) соответственно.
-
Введем ограничения для переменных:
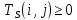 (1)
(1) 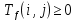 (2)
(2)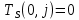 (3)
(3)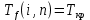 (4)
(4)здесь n – номер завершающего события (n=20, ????кр = 62,675).
Условие последовательности работ выражается следующей формулой:
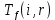 −
− 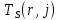 ≤ 0 (5)
≤ 0 (5)(
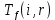 ≤
≤ 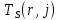 )
)Иначе говоря, работа, выходящая из события r не может начаться раньше, чем закончится работа, входящая в событие r.
Распишу условие 5 для каждой пары работ:
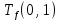 −
− 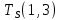 ≤ 0
≤ 0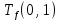 −
− 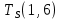 ≤ 0
≤ 0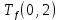 −
− 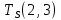 ≤ 0
≤ 0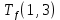 −
− 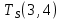 ≤ 0
≤ 0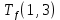 −
− 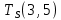 ≤ 0
≤ 0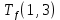 −
− 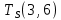 ≤ 0
≤ 0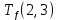 −
− 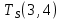 ≤ 0
≤ 0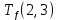 −
− 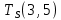 ≤ 0
≤ 0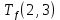 −
− 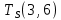 ≤ 0
≤ 0 −
− 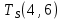 ≤ 0
≤ 0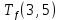 −
− 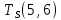 ≤ 0
≤ 0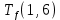 −
− 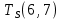 ≤ 0
≤ 0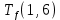 −
− 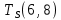 ≤ 0
≤ 0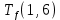 −
− 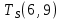 ≤ 0
≤ 0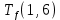 −
− 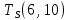 ≤ 0
≤ 0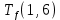 −
− 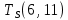 ≤ 0
≤ 0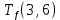 −
− 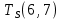 ≤ 0
≤ 0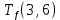 −
− 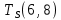 ≤ 0
≤ 0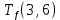 −
− 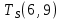 ≤ 0
≤ 0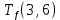 −
− 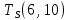 ≤ 0
≤ 0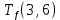 −
− 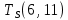 ≤ 0
≤ 0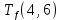 −
− 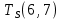 ≤ 0
≤ 0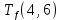 −
− 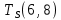 ≤ 0
≤ 0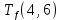 −
− 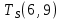 ≤ 0
≤ 0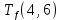 −
− 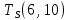 ≤ 0
≤ 0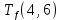 −
− 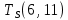 ≤ 0
≤ 0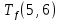 −
− 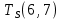 ≤ 0
≤ 0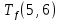 −
− 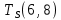 ≤ 0
≤ 0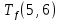 −
− 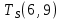 ≤ 0
≤ 0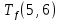 −
− 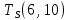 ≤ 0
≤ 0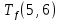 −
− 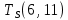 ≤ 0
≤ 0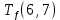 −
− 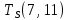 ≤ 0
≤ 0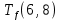 −
− 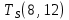 ≤ 0
≤ 0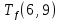 −
− 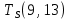 ≤ 0
≤ 0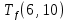 −
− 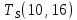 ≤ 0
≤ 0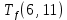 −
−  ≤ 0
≤ 0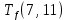 −
−  ≤ 0
≤ 0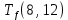 −
− 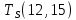 ≤ 0
≤ 0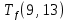 −
− 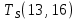 ≤ 0
≤ 0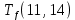 −
− 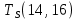 ≤ 0
≤ 0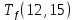 −
− 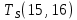 ≤ 0
≤ 0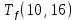 −
− 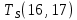 ≤ 0
≤ 0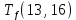 −
− 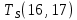 ≤ 0
≤ 0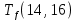 −
− 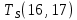 ≤ 0
≤ 0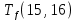 −
− 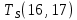 ≤ 0
≤ 0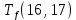 −
− 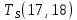 ≤ 0
≤ 0 −
− 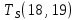 ≤ 0
≤ 0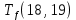 −
− 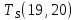 ≤ 0
≤ 0