Файл: Курсовая работа по дисциплине Математика Тема Математические методы и модели исследования операций.docx
Добавлен: 07.12.2023
Просмотров: 59
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Совокупность неравенств такого вида аналитически отражает сетевой график. Время выполнения работы, то есть разность между значениями
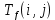 и
и 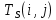 для одной работы должна быть не меньше минимально возможного времени выполнения этой работы:
для одной работы должна быть не меньше минимально возможного времени выполнения этой работы: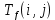 −
− 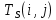 ≥
≥ 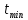 (????, ????),
(????, ????), 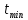 (????, ????) известно (6)
(????, ????) известно (6)Время выполнения работы, то есть разность между значениями
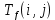 и
и 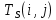 для одной работы должна быть не больше максимально возможного времени выполнения этой работы:
для одной работы должна быть не больше максимально возможного времени выполнения этой работы: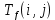 −
− 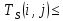
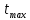 (????, ????),
(????, ????), 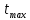 (????, ????) известно (7)
(????, ????) известно (7)Распишу условия 6 и 7:
 −
− 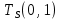 ≥4,8
≥4,8 −
− 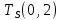 ≥3,8
≥3,8 −
−  ≥0
≥0 −
−  ≥4,3
≥4,3 −
−  ≥13,3
≥13,3 −
−  ≥3,3
≥3,3 −
−  ≥2,8
≥2,8 −
−  ≥3,3
≥3,3 −
−  ≥0,33
≥0,33 −
−  ≥0,33
≥0,33 −
−  ≥0,73
≥0,73 −
−  ≥0,53
≥0,53 −
−  ≥0,63
≥0,63 −
− 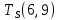 ≥5,3
≥5,3 −
−  ≥6,3
≥6,3 −
−  ≥0
≥0 −
−  ≥0,93
≥0,93 −
−  ≥0,63
≥0,63 −
−  ≥6,3
≥6,3 −
−  ≥3,65
≥3,65 −
−  ≥2,65
≥2,65 −
−  ≥0
≥0 −
−  ≥0
≥0 −
−  ≥0
≥0 −
−  ≥0,63
≥0,63 −
−  ≥3,65
≥3,65 −
−  ≥3,65
≥3,65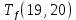 −
−  ≥11,3
≥11,3 −
− 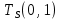 ≤8,1
≤8,1 −
− 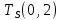 ≤7,1
≤7,1 −
−  ≤0
≤0 −
−  ≤7,6
≤7,6 −
−  ≤17,1
≤17,1 −
−  ≤6,1
≤6,1 −
−  ≤6,1
≤6,1 −
−  ≤4,6
≤4,6 −
−  ≤0,66
≤0,66 −
−  ≤0,56
≤0,56 −
−  ≤0,96
≤0,96 −
−  ≤0,63
≤0,63 −
−  ≤0,745
≤0,745 −
− 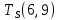 ≤7,6
≤7,6 −
−  ≤9,6
≤9,6 −
−  ≤0
≤0 −
−  ≤1,13
≤1,13 −
−  ≤0,83
≤0,83 −
−  ≤10,6
≤10,6 −
−  ≤6,26
≤6,26 −
−  ≤5,26
≤5,26 −
−  ≤0
≤0 −
−  ≤0
≤0 −
−  ≤0
≤0 −
−  ≥0,73
≥0,73 −
−  ≤4,65
≤4,65 −
−  ≤4,65
≤4,65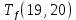 −
−  ≤14,6
≤14,6-
Введем в рассмотрение целевую функцию, показывающую сумму затрат:
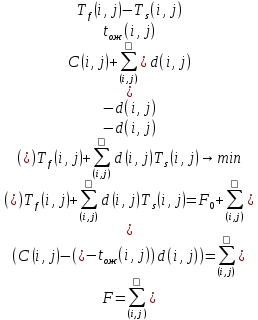
Так как в программе Microsoft Excel существует ограничение на количество переменных в задаче, воспользуюсь аналогичной программой LibreOffice calc, которая такого недостатка не имеет.
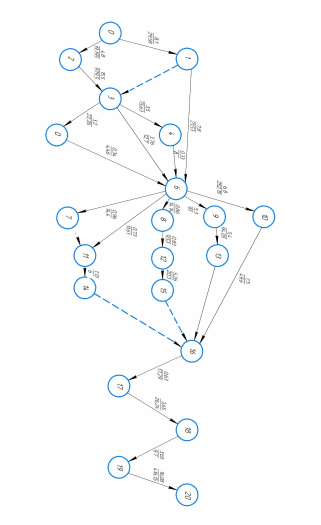
В результате решения получили время начала и окончания каждой работы. Отняв из времени окончания работы время её начала, мы получим длительность работы. Именно при такой длительности каждой работы можно достичь минимальной стоимости выполнения сетевого плана. Проиллюстрирую полученные результаты на сетевом графике (приложение А). При таких параметрах сетевого плана его стоимость будет минимальна и равна 2208,331.
3.5 Оптимизация сетевого плана по критерию «время»
Построим модель линейного программирования для решения данной задачи:
-
Введём переменные. Пусть Ts(i, j) и Tf(i, j) - время (сроки), дни, начала и окончания работы (i,j) соответственно. Х(i,j) – фактическая стоимость работы (i,j) (в результате оптимизации) -
Введем фиктивную работу (n, n+1).
Время выполнения и стоимость фиктивной работы равны нулю t(n, n+1) = 0, С(n, n+1) = 0 (1)
-
Введем ограничения для переменных:
????????(????, ????) ≥ 0 (2)
???????? (????, ????) ≥ 0 (3)
????????(0, ????) = 0 (4)
???????? (20, 21) ≤ ????кр (5)
Х(i,j)≥ 0 (6)
-
Общая стоимость работ равна имеющейся первоначально:
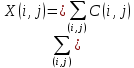
Условие последовательности работ выражается следующей формулой:
???????? (????, ????) − ????????(????, ????) ≤ 0 (8)
Время выполнения работы, то есть разность между значениями
 и
и  для одной работы должна быть не меньше минимально возможного времени выполнения этой работы:
для одной работы должна быть не меньше минимально возможного времени выполнения этой работы:???????? (????, ????) − ????????(????, ????) ≥ tmin(????, ????) tmin(????, ????) известно (9)
Время выполнения работы, то есть разность между значениями
 и
и  для одной работы должна быть не больше максимально возможного времени выполнения этой работы:
для одной работы должна быть не больше максимально возможного времени выполнения этой работы:???????? (????, j) − ????????(i, ????) ≤ tmах(????, ????) tmах(????, ????) известно (10)
-
Введем условие, связывающее переменные задачи:
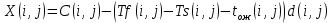
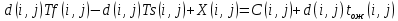
-
Введем в рассмотрение целевую функцию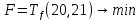 .
.
В результате решения получили время начала и окончания каждой работы, а также стоимость выполнения каждой работы. Отняв из времени окончания работы время её начала, мы получим длительность работы. Проиллюстрирую полученные результаты на сетевом графике (приложение Б). При таких параметрах сетевого плана время его выполнения будет минимально и равно 54,69, что
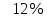 меньше, а его стоимость будет равна 2186,8.
меньше, а его стоимость будет равна 2186,8.3.5Оптимизация сетевого плана по критерию «время-стоимость»
Построим модель линейного программирования для решения данной задачи:
-
Введём переменные. Пусть Ts(i, j) и Tf(i, j) - время (сроки), дни, начала и окончания работы (i,j) соответственно. Х(i,j) – фактическая стоимость работы (i,j) (в результате оптимизации) -
Введем фиктивную работу (n, n+1).
Время выполнения и стоимость фиктивной работы равны нулю t(n, n+1) = 0, С(n, n+1) = 0 (1)
-
Введем ограничения для переменных:
????????(????, ????) ≥ 0 (2)
???????? (????, ????) ≥ 0 (3)
????????(0, ????) = 0 (4)
???????? (20, 21) =
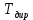 (5)
(5)Х(i,j)≥ 0 (6)
Вычислю значение директивного времени для каждого случая, округляя значения до целого с избытком:
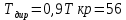
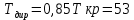
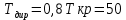
-
Общая стоимость работ равна имеющейся первоначально:

Условие последовательности работ выражается следующей формулой:
???????? (????, ????) − ????????(????, ????) ≤ 0 (8)
Время выполнения работы, то есть разность между значениями
 и
и  для одной работы должна быть не меньше минимально возможного времени выполнения этой работы:
для одной работы должна быть не меньше минимально возможного времени выполнения этой работы:???????? (????, ????) − ????????(????, ????) ≥ tmin(????, ????) tmin(????, ????) известно (9)
Время выполнения работы, то есть разность между значениями

и
 для одной работы должна быть не больше максимально возможного времени выполнения этой работы:
для одной работы должна быть не больше максимально возможного времени выполнения этой работы:???????? (????, j) − ????????(i, ????) ≤ tmах(????, ????) tmах(????, ????) известно (10)
-
Введем условие, связывающее переменные задачи:


-
Введем в рассмотрение целевую функцию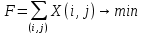
В результате решения получили время начала и окончания каждой работы, а также стоимость выполнения каждой работы. Отняв из времени окончания работы время её начала, мы получим длительность работы. Проиллюстрирую полученные результаты на сетевом графике (приложение В). При таких параметрах сетевого плана время его выполнения будет точно соответствовать директивному, а его стоимость будет равна 2167,903, что на 2% меньше, при
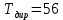 ,
, При
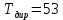 стоимость равна 2226,817, что на 1% больше
стоимость равна 2226,817, что на 1% большеПри
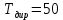 решение не было найдено. Определю минимальное время выполнения плана без ограничений на стоимость. В результате решения получил значение 50,99.
решение не было найдено. Определю минимальное время выполнения плана без ограничений на стоимость. В результате решения получил значение 50,99.Так как длительность выполнения сетевого плана характеризуется длинной критического пути, при уменьшении общего времени выполнения плана необходимо уменьшать в первую очередь длительность работ, лежащих на критическом пути, что и следует из решения. При уменьшении времени выполнения работ закономерно возрастает стоимость их выполнения, соответственно, и стоимость всего плана.
Заключение
При выполнении курсовой работы мною были получены и закреплены теоретические и практические умения решения задач прикладного характера с использованием методов исследования операций.
В ходе выполнения данной курсовой работы было произведено решение прямой задачи, по минимизации общей стоимости продукции. Результат получен с помощью Microsoft Excel. Составлен сетевой график, с последующим нахождением временных параметров и вероятностных характеристик. Проведена оптимизация по критериям «стоимость», «время» и «стоимость-время».
Курсовая работа по данной дисциплине расширила мои знания в сфере математической оптимизации различных задач. Полученные навыки, несомненно, способствуют более легкому дальнейшему обучению.
Список литературы
-
Вагнер, Г. Основы исследования операций / Г. Вагнер. – М.: Мир, 1972. –
Т.1. – 335 с.
-
Майника, Э. Алгоритмы оптимизации на сетях и графах / Э. Майника. – М.: Мир, 1981. – 312 с. -
Исследование операций. Модели и применение. / Под ред. Дж. Моудера. – М.: Мир, 1981. – Т.2.− 514 c. -
Моудер, Дж. Метод сетевого планирования в организации работ / Дж. Моудер, С.Филлипс. – М.: Энергия, 1976. – 473 с. -
Плескунов, М.А. Задачи сетевого планирования : учебное пособие / М. А.
Плескунов. – Екатеринбург : Изд-во Урал. Ун-та, 2014. – 92 с.
-
Таирова, Е.В. Методы сетевого планирования в организации комплексов работ: учебное пособие / Е.В. Таирова. – Иркутск: ИрГУПС, 2007. – 95 с. -
Таха, Х.А. Введение в исследование операции / Х.А. Таха – 7-е издание. – М.: Вильямс, 2005. – 912 с. -
Семенов, В.А. Комплексный метод составления расписаний для сложных индустриальных программ с учетом пространственно-временных ограничений / В.А. Семенов, А.С. Аничкин, С.В. Морозов, О.А. Тарлапан, В.А. Золотов // Труды Института системного программирования РАН, 2014. – 16 с.
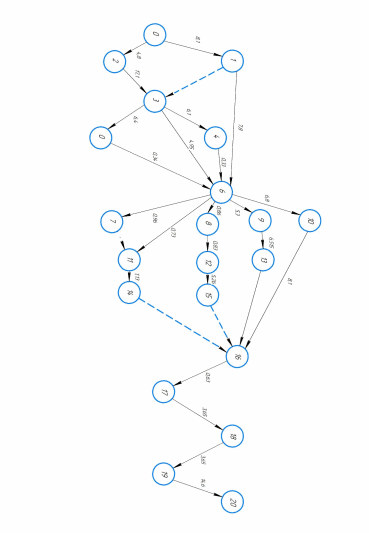 ПРИЛОЖЕНИЕ А
ПРИЛОЖЕНИЕ АПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ Б
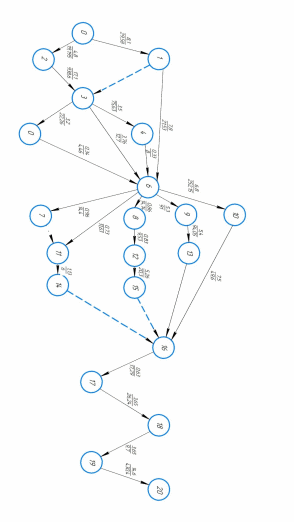
ПРИЛОЖЕНИЕ В
Директивное время 56
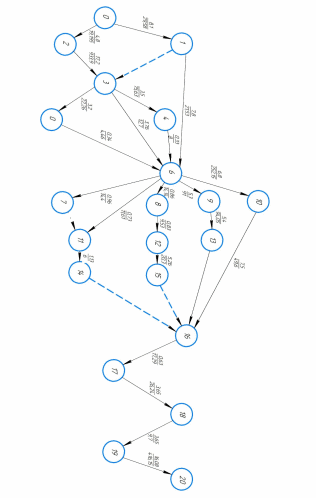
Директивное время 53