ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Свойство 3. Математическое ожидание постоянной величины равно самой постоянной:
Свойство 4. Постоянный множитель случайной величины можно вынести за знак математического ожидания:
Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
-
Дисперсия С.В. и ее свойства.
В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины X и обозначают D[X]:
Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующие вероятности:
Для непрерывной случайной величины, закон распределения которой задан плотностью распределения вероятности f(x), дисперсия
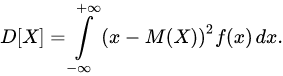
Размерность дисперсии равна квадрату размерности случайной величины и поэтому ее нельзя интерпретировать геометрически. Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое вычисляется по формуле
Свойства дисперсии случайных величин:
Свойство 1. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Свойство 2. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:
Свойство 3. Дисперсия постоянной величины равна нулю:
Свойство 4. Постоянный множитель случайной величины, можно выносить за знак дисперсии, предварительно возведя его в квадрат:
Свойство 5. Дисперсия произведения двух независимых случайных величин X и Y определяется по формуле
-
Равномерный и нормальный закон распределения, стандартная форма нормального закона распределения С.В.
Равномерный закон распределения
Случайная величина X называется распределённой равномерно на отрезке [a; b], если её плотность распределения вероятностей постоянна на данном отрезке:
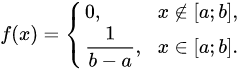
Все возможные значения равномерно распределённой случайной величины лежат в пределах некоторого интервала; кроме того. в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности). Равномерно распределение реализуется в экспериментах, где наудачу ставиться точка на отрезке [a; b] (X — абсцисса поставленной точки).
Математическое ожидание и дисперсия равномерно распределённой случайной величины
Характеристическая функция равномерного распределения задаётся формулой
График плотности равномерного распределения
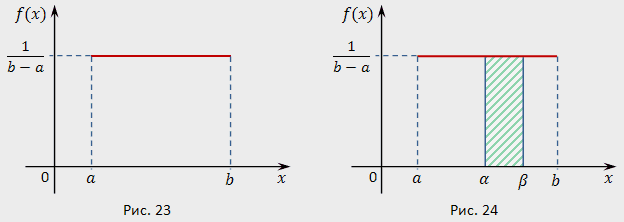
Нормальный закон распределения (закон Гаусса)
Плотность вероятности нормально распределённой случайной величины X выражается формулой
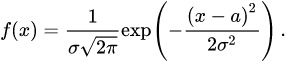
Кривая распределения изображена на рисунке. Она симметрична относительно точки x=a (точка максимума). При уменьшении ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы.
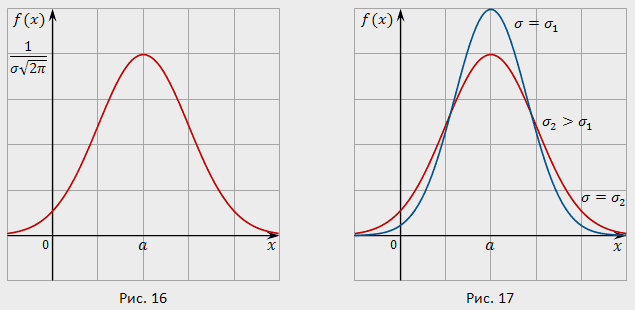
Математическое ожидание и дисперсия нормально распределённой случайной величины:
Нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины:
Характеристическая функция нормального распределения случайной величины задаётся формулой
Стандартная форма нормального закона распределения С.В.:
Нормальный закон распределения с параметрами и называется стандартным или нормированным и обозначается :
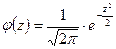.16. Распределение Пирсона, t-распределение Стьюдента, F-распределение Фишера. Показательный закон распределения.
Распределение Пирсона — непрерывное распределение вероятностей, плотность вероятности которого является решением дифференциального уравнения
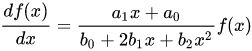, где числа 
являются параметрами распределения.t-распределение Стьюдента (или просто t-распределение) - это любой член семейства непрерывных вероятностных распределений, возникающих при оценке среднего значения нормально распределенной популяции в ситуациях, когда размер выборки мал, а стандартное отклонение популяции неизвестно.
Пусть
— независимые стандартные нормальные случайные величины, такие что 
Тогда распределение случайной величины t, где 
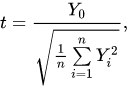называется распределением Стьюдента с степенями свободы 
.F–распределение Снедекора или распределение Фишера-Снедекора, представляет собой непрерывное распределение вероятностей, которое часто возникает как нулевое распределение тестовой статистики.
F-распределение с d1 и d2 степенями свободы является распределением:
, где S1 и S2 - независимые случайные величины с распределениями хи-квадрат с соответствующими степенями свободы d1 и d2.Показательный (экспоненциальный закон распределения).
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
Функция распределения имеет вид:
Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
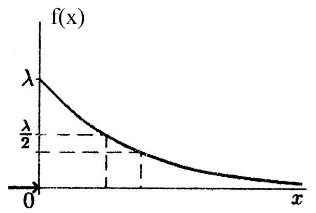
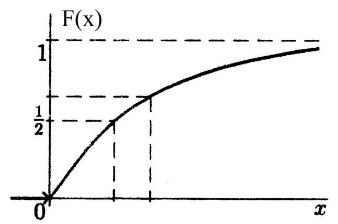
То есть при
-
Структурные характеристики распределения С.В.
К структурным характеристикам относятся такие характеристики, как начальные и центральные моменты. Структурные характеристики определяют некоторые свойства случайных величин.
Начальный момент порядка k случайной величины Х:
Для дискретной случайной величины начальный момент k порядка
, где - вероятность, - значение случайной величины.
Для непрерывной случайной величины, имеющей плотность вероятности , начальный момент k порядка
.Центральный момент случайной величины Х –величина, которая определяется как
.Особое значение имеют такие показателиначального и центрального моменты, которые называются коэффициент ассиметрии и коэффициент эксцесса
Для нормального распределения справедливо: 0, 0.
18. Системы С.В. Закон распределения системы (X, Y). Маржинальный закон распределения С.В.
Системы случайных величин
Если рассмотреть совместно две случайных величины ξ и η, то можно считать, что рассматривается система случайных величин. Геометрически пара случайных величин ξ и η может быть представлена как случайная точка M (x, y) на плоскости.