ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 145
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Законы распределения систем случайных величин
Закон распределения системы случайных величин – функция, которая ставит в соответствие любой паре значений случайных величин ξ и η вероятность её появления
P: [0,1].
Маржинальный закон распределения случайной величины
В дискретном случае вероятности распределяются по формулам:
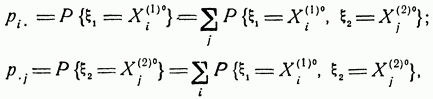
19. Интегральный закон распределения системы С.В. и его свойства. Плотность вероятности системы С.В. Маржинальные плотности системы С.В.
Интегральная функция распределения вероятностей системы случайных величин:
и геометрически представляет собой вероятность попадания случайной точки с координатами (Х, У) в бесконечный прямоугольник с вершиной в точке М(х;у), лежащий левее и ниже ее.Свойства интегральной функции распределения:
1)
2)
3)
4)
Для систем дискретных случайных величин интегральная функция распределения:
Свойства дифференциальной функции распределения (плотности вероятности):
1)
2)
(условие нормировки);3)
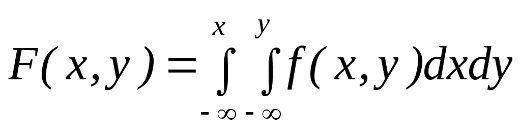
4) вероятность попадания случайной точки (Х, Y) в область D:
Маржинальные плотности системы случайных величин
Для непрерывных случайных величин маргинальную функцию плотности вероятности можно записать как pX(x).
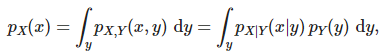
20. Условный закон распределения системы С.В.
Если случайные величины, образующие систему, зависимы, то для нахождения закона распределения системы недостаточно знать законы распределения отдельных величин, входящих в систему. Требуется еще знать так называемый условный закон распределения одной из них.
Условным законом распределения одной из величин, входящих в систему, называется ее закон распределения, вычисленный при условии, что другая случайная величина приняла определенное значение. Пусть случайная величина Y является дискретной.
Условной функцией распределения
случайной величины X при условии называется условная вероятность события при условии события , т.е. 
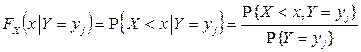.Аналогично определяется условная функция распределения
случайной величины Y при условии (когда случайная величина X является дискретной): 
.21. Математическое ожидание и дисперсия системы случайных величин.
Математическим ожиданием двумерной случайной величины называется совокупность двух математических ожиданий М[Х], М[Y],то есть упорядоченных пар М[Х], М[Y],которые определяются равенствами:
а) если Х и Y– дискретные случайные величины:
М[Х]=
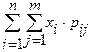, : ; .М[Y]=
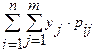.б) если Х и Y– непрерывные случайные величины:
М[Х]=
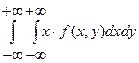
М[Y]=
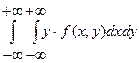,где - плотность вероятности двумерной случайной величины .
Математическое ожидание случайной величины , которая является функцией компонент двумерной случайной величины , находится аналогично по формулам:
1) М [j (Х, Y)] =
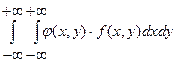
- если Хи Y– непрерывные случайные величины;
2) М [j (Х, Y)] =
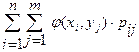, : ; - если Хи Y– дискретные случайные величины.Дисперсиядвумерной случайной величины - совокупность двух дисперсий D[X] и D[Y], которые определяются равенствами:
а) если Х и Y– дискретные случайные величины:
D[X]=
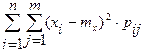, : ; .D[Y]=
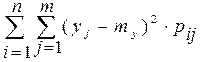.б) если Х и Y– непрерывные случайные величины:
D[X]=
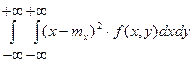
D[Y]=
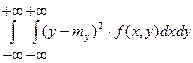,где - плотность вероятности двумерной случайной величины ,
, - математические ожидания компонент .
22. Условное математическое ожидание системы С.В.
Пусть (X, Y) – система дискретных случайных величин. Условным математическим ожиданием дискретной случайной величины Y при условии, что Х= , называется величина
М[Y│X= ]=
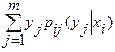.Аналогично, условным математическим ожиданием дискретной случайной величины X при условии, что Y=yj, называется величина
М[Х│Y= ]=
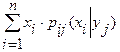, : ; .Пусть - система непрерывных случайных величин. В этом случае условное математическое ожидание случайной величины Y при условии, что Х=xi, определяется равенством:
М[Y│ ]=
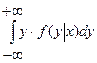.Аналогично, условное математическое ожидание случайной величины X при условии, что Y=yj, определяется равенством:
М[Х│ ]=
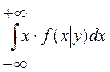
23. Корреляционный момент и коэффициент корреляции.
Для характеристики связи между величинами Х и Y (22-й вопрос) служит корреляционный момент
:
Kxy=М [ ]=M [(X – mx) M (Y – my)].
Используя понятие корреляционного момента, запишем еще одно свойство дисперсии, а именно - дисперсия суммы двух случайных величин определяется равенством:
D[X+Y] = D[X]+D[Y]+2Kxy
Корреляционный момент иначе называется ковариация и обозначается cov(Х, Y).
Величина корреляционного момента вычисляется по формулам:
а) если Хи Y– дискретные случайные величины:
Kxy=
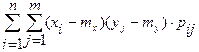, : ; .б) если Хи Y– непрерывные случайные величины:
Kxy=
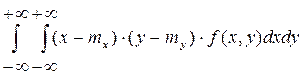,где - плотность вероятности двумерной случайной величины ,
, - математические ожидания компонент .
Корреляционный момент удобно вычислять по формуле:
Kxy=М[ХY]-М[Х]М[Y].
Если Хи Y независимы, то Kxy=0.Таким образом, если Kxy 0, то случайные величины Хи Y зависимы. В этом случае случайные величины Хи Y называются коррелированными.
Когда Kxy=0, случайные величины Хи Y называются некоррелированными.
Из рассмотренного свойства корреляционного момента получаем важное следствие. Дисперсия суммы двух случайных величин равна сумме их дисперсий если величины X и Y независимы, т.е.
D[X+Y] = D[X]+D[Y]+2Kxy
Коэффициент корреляции (rxy)для двух случайных величин Хи Y есть безразмерная величина:
rxy= ,
где , - средние квадратические отклонения величин Хи Y соответственно.
Коэффициент корреляции характеризует степень линейной зависимости двух случайных величин Х и Y.
24. Функции одной и двух случайных величин.
Функция одной случайной величины.
Свойства коэффициента корреляции.
1. rxy Î [-1,1].
2. Если Хи Y независимы, то rxy=0.
3. Если Хи Y связаны линейной зависимостью вида Y=а+b×X, то rxy=1.
4. Если çrxy ÷=1, то случайные величины Хи Y связаны линейной функциональной зависимостью:
прямой