ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 146
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– если rxy=1, обратной - если rxy=-1.
Пусть рассматриваются две случайные величины Х и Y, которые связаны функциональной зависимостью вида Y=j (X).
Если Х– дискретная случайная величина, закон распределения которой определяется формулой
,
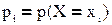то случайная величина Y также дискретна, а её закон распределения выражается следующим образом:
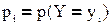, где yi = φ(xi), а = .
Математическое ожидание и дисперсия случайной величины Y вычисляется по формулам:
для дискретной случайной величины
М[Y]=М [j (X)] =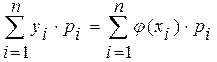
,
D[Y] = D [[j (X)] = Σ (yi – my)2 pi = Σ (j (xi) – my)2 pi
и для непрерывной случайной величины
М[Y]=М [j (X)] =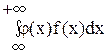
D[Y]=D [j (X)] =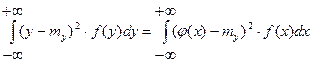
.
Функция двух случайных величин
Пусть рассматривается система двух случайных величин . Если каждой паре возможных значений случайных величин соответствует одно возможное значение Z= , которое находится по определённому закону, то случайная величина Z называется функцией двух случайных аргументов .
Для функции двух и более случайных аргументов удобнее сначала находить функцию распределения G(z), а затем плотность вероятности g(z):
.
Если - система дискретных случайных величин, то
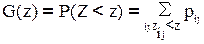, где 
.
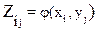Если - система непрерывных случайных величин, то
,
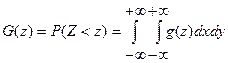где - плотность распределения случайной величины Z.
Важное значение имеет задача определения закона распределения суммы двух случайных величин: Z=Х+Y. Плотность распределения этой суммы равна:
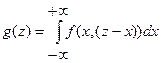
или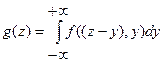
Если случайные величины Хи Yнезависимы, то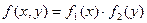
, и можно записать:
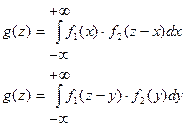или где , - плотности распределения случайных величин Хи Y.
25. Случайные функции. Математическое ожидание и дисперсия случайной функции и их свойства.
Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении t является случайной величиной. Если аргументом случайной функции является время, то случайная функция называется случайным процессом.
Математическим ожиданием случайной функции X(t) называют неслучайную функцию mx(t), значение которой при каждом фиксированном значении аргумента равно математическому ожиданию сечения, соответствующего этому же значению аргумента:
mx(t)=М[X(t)].
Свойство 1. Математическое ожидание неслучайной функции φ(t)(О равно самой неслучайной функции: М[φ(t)]=φ(t).
Свойство 2. Неслучайный множитель φ(t) можно выносить за знак математического ожидания: М[φ(t)Х(t)]=φ(t)М[X(t)]=φ(t)тx(t).
Свойство 3. Математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых: M[X(t)+Y(t)]=mx(t)+my(t).
Дисперсией случайной функции Х(t) называют неслучайную неотрицательную функцию Dx(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии сечения, соответствующего этому же фиксированному значению аргумента:
Dx(t)=D[X(t)].
Свойство 1. Дисперсия неслучайной функции φ(t) равна нулю: D[φ(t)]=0.
Свойство 2. Дисперсия суммы случайной функции Х(t) и неслучайной функции φ(t) равна дисперсии случайной функции: D[X(t)+φ(t)]=Dx(t).
Свойство 3. Дисперсия произведения случайной функции Х(t) на неслучайную функцию φ(t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции:
D[X(t)φ(t)]=φ2(t)Dx(t).
26. Корреляционная функция случайной функции и ее свойства. Нормированная корреляционная функция.
Корреляционной функцией случайной функции Х(t)называют неслучайную функцию Кх(t1,t2) двух независимых аргументов t1 и t2, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:
Кх(t1,t2)=M[ (t1)(t2)].
Замечание. При равных между собой значенияхаргументов t1=t2=t корреляционная функция случайной функцииравна дисперсии этой функции: Кх(t,t)=Dx(t)
Действительно, учитывая, что Dx(t)=M[X(t)-mx(t)]2=M[ (t)]2, получим
Кх(t,t)= M[ (t)(t)]=М [ (t)]2=Dx(t).
Таким образом, достаточно знать корреляционную функцию, чтобы найти дисперсию случайной функции.
Свойство 1.При перестановке аргументов корреляционная функция не изменяется (свойство симметрии): Кх(t1,t2)= Кх(t2,t1).
Свойство 2.Прибавление к случайной функции Х(t) неслучайного слагаемого φ(t) не изменяет ее корреляционной функции: если Y(t)=X(t)+φ(t), то Кy(t1,t2)= Кх(t1,t2).
Свойство3.Приумножении случайной функции Х(t) нанеслучайный множитель φ(t)еекорреляционная функция умножается на произведение
φ(t1) φ(t2):
если (t)= (t)φ(t). то Кy(t1,t2)= Кх(t1,t2) φ(t1) φ(t2).
Свойство 4.Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений: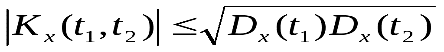
.
Нормированной корреляционной функцией случайной функции Х(t) называют неслучайную функцию двух независимых переменных t1 и t2, значение которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:
(*)
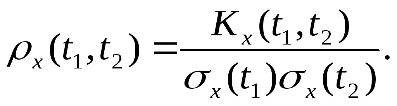Учитывая, что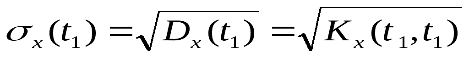
и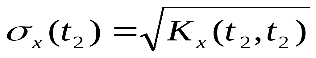 
,получим
(*)
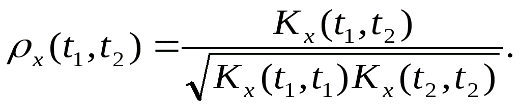Таким образом, зная корреляционную функцию, можно найти нормированную корреляционную функцию.
27. Взаимные корреляционные функции двух случайных функций и их свойства. Нормированные взаимные корреляционные функции.
Взаимной корреляционной функцией двух случайных функций Х(t) и Y(t) называют неслучайную функцию Rxy(t1,t2) двух независимых аргументов t1и t2 значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений обеих функций, соответствующих этим же фиксированным значениям аргументов:
Rxy (t1, t2) = M[ (t1)(t2)].
Коррелированными называют две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю.
Свойство 1.При одновременной перестановке индексов и аргументов взаимная корреляционная функция не изменяется:Rxy(t1,t2)= Ryx(t2,t1).
Свойство 2.Прибавление к случайным функциям Х(t) и Y(t) неслучайных слагаемых, соответственно φ(t)и ψ(t), не изменяет их взаимной корреляционной функции:
если
X1(t)=X(t)+φ(t)и Y1(t)=Y(t)+ψ(t), то Rx1y2(t1,t2)= Rxy(t1,t2).
Свойство 3.При умножении случайных функций Х(t)и У(t) на неслучайные множители, соответственно φ(t)и ψ(t), взаимная корреляционная функция умножается на произведениеφ(t1)ψ(t2):
если
X1(t)=X(t)φ(t)и Y1(t)=Y(t)+ψ(t
Пусть рассматриваются две случайные величины Х и Y, которые связаны функциональной зависимостью вида Y=j (X).
Если Х– дискретная случайная величина, закон распределения которой определяется формулой
,то случайная величина Y также дискретна, а её закон распределения выражается следующим образом:
, где yi = φ(xi), а = .Математическое ожидание и дисперсия случайной величины Y вычисляется по формулам:
для дискретной случайной величины
М[Y]=М [j (X)] =
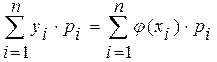,D[Y] = D [[j (X)] = Σ (yi – my)2 pi = Σ (j (xi) – my)2 pi
и для непрерывной случайной величины
М[Y]=М [j (X)] =
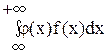
D[Y]=D [j (X)] =
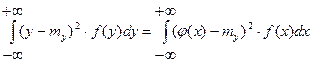.Функция двух случайных величин
Пусть рассматривается система двух случайных величин . Если каждой паре возможных значений случайных величин соответствует одно возможное значение Z= , которое находится по определённому закону, то случайная величина Z называется функцией двух случайных аргументов .
Для функции двух и более случайных аргументов удобнее сначала находить функцию распределения G(z), а затем плотность вероятности g(z):
.
Если - система дискретных случайных величин, то
, где .Если - система непрерывных случайных величин, то
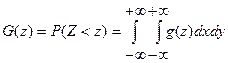,где - плотность распределения случайной величины Z.
Важное значение имеет задача определения закона распределения суммы двух случайных величин: Z=Х+Y. Плотность распределения этой суммы равна:
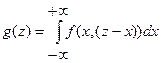
или
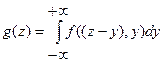
Если случайные величины Хи Yнезависимы, то
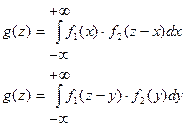, и можно записать: или где , - плотности распределения случайных величин Хи Y.25. Случайные функции. Математическое ожидание и дисперсия случайной функции и их свойства.
Случайной функцией X(t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении t является случайной величиной. Если аргументом случайной функции является время, то случайная функция называется случайным процессом.
Математическим ожиданием случайной функции X(t) называют неслучайную функцию mx(t), значение которой при каждом фиксированном значении аргумента равно математическому ожиданию сечения, соответствующего этому же значению аргумента:
mx(t)=М[X(t)].
Свойство 1. Математическое ожидание неслучайной функции φ(t)(О равно самой неслучайной функции: М[φ(t)]=φ(t).
Свойство 2. Неслучайный множитель φ(t) можно выносить за знак математического ожидания: М[φ(t)Х(t)]=φ(t)М[X(t)]=φ(t)тx(t).
Свойство 3. Математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых: M[X(t)+Y(t)]=mx(t)+my(t).
Дисперсией случайной функции Х(t) называют неслучайную неотрицательную функцию Dx(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии сечения, соответствующего этому же фиксированному значению аргумента:
Dx(t)=D[X(t)].
Свойство 1. Дисперсия неслучайной функции φ(t) равна нулю: D[φ(t)]=0.
Свойство 2. Дисперсия суммы случайной функции Х(t) и неслучайной функции φ(t) равна дисперсии случайной функции: D[X(t)+φ(t)]=Dx(t).
Свойство 3. Дисперсия произведения случайной функции Х(t) на неслучайную функцию φ(t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции:
D[X(t)φ(t)]=φ2(t)Dx(t).
26. Корреляционная функция случайной функции и ее свойства. Нормированная корреляционная функция.
Корреляционной функцией случайной функции Х(t)называют неслучайную функцию Кх(t1,t2) двух независимых аргументов t1 и t2, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:
Кх(t1,t2)=M[ (t1)(t2)].
Замечание. При равных между собой значенияхаргументов t1=t2=t корреляционная функция случайной функцииравна дисперсии этой функции: Кх(t,t)=Dx(t)
Действительно, учитывая, что Dx(t)=M[X(t)-mx(t)]2=M[ (t)]2, получим
Кх(t,t)= M[ (t)(t)]=М [ (t)]2=Dx(t).
Таким образом, достаточно знать корреляционную функцию, чтобы найти дисперсию случайной функции.
Свойство 1.При перестановке аргументов корреляционная функция не изменяется (свойство симметрии): Кх(t1,t2)= Кх(t2,t1).
Свойство 2.Прибавление к случайной функции Х(t) неслучайного слагаемого φ(t) не изменяет ее корреляционной функции: если Y(t)=X(t)+φ(t), то Кy(t1,t2)= Кх(t1,t2).
Свойство3.Приумножении случайной функции Х(t) нанеслучайный множитель φ(t)еекорреляционная функция умножается на произведение
φ(t1) φ(t2):
если (t)= (t)φ(t). то Кy(t1,t2)= Кх(t1,t2) φ(t1) φ(t2).
Свойство 4.Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений:
.Нормированной корреляционной функцией случайной функции Х(t) называют неслучайную функцию двух независимых переменных t1 и t2, значение которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:
(*)Учитывая, что
и ,получим (*)Таким образом, зная корреляционную функцию, можно найти нормированную корреляционную функцию.
27. Взаимные корреляционные функции двух случайных функций и их свойства. Нормированные взаимные корреляционные функции.
Взаимной корреляционной функцией двух случайных функций Х(t) и Y(t) называют неслучайную функцию Rxy(t1,t2) двух независимых аргументов t1и t2 значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений обеих функций, соответствующих этим же фиксированным значениям аргументов:
Rxy (t1, t2) = M[ (t1)(t2)].
Коррелированными называют две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю.
Свойство 1.При одновременной перестановке индексов и аргументов взаимная корреляционная функция не изменяется:Rxy(t1,t2)= Ryx(t2,t1).
Свойство 2.Прибавление к случайным функциям Х(t) и Y(t) неслучайных слагаемых, соответственно φ(t)и ψ(t), не изменяет их взаимной корреляционной функции:
если
X1(t)=X(t)+φ(t)и Y1(t)=Y(t)+ψ(t), то Rx1y2(t1,t2)= Rxy(t1,t2).
Свойство 3.При умножении случайных функций Х(t)и У(t) на неслучайные множители, соответственно φ(t)и ψ(t), взаимная корреляционная функция умножается на произведениеφ(t1)ψ(t2):
если
X1(t)=X(t)φ(t)и Y1(t)=Y(t)+ψ(t