ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 148
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Такая оценка, называемая оценкой максимальной правдоподобия, является решением уравнения
(29)
.Из курса математического анализа известно, что функции
и
достигают своего максимума при одном и том же значении (самостоятельно убедитесь в этом), то вместо отыскания максимального значения функции ищут (что проще, где в правых частях равенств (27) и (28) каждое произведение превращается сумму слагаемых) максимум функции 
Таким образом, для нахождения оценки максимального правдоподобия необходимо:
1. решить уравнение правдоподобия
(30)
2. следует отобрать то решение, которое обращает функцию
в максимум, при этом удобно использовать вторую производную: если(31)
то точкой максимума будет
.В случаях, когда подлежат оценке несколько параметров
распределения, то оценки
определяются решением системы уравнений правдоподобия;
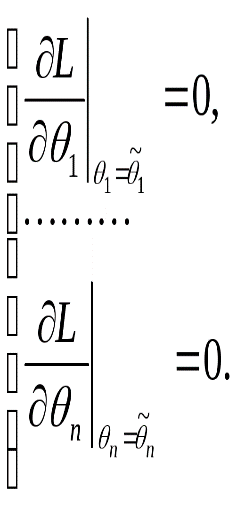
32. Метод наименьших квадратов.
Имеются результаты независимых измерений - опытные точки
Из теоретических или иных соображений, с точностью до количества (или других признаков) неизвестных параметров (здесь мы ограничимся двумя) и известна функциональная зависимость от в виде(35)
.Экспериментальные точки уклоняются от этой зависимости вследствие неизбежных ошибок измерений. Как правило, эти ошибки распределены по нормальному закону. Рассмотрим некоторое значение независимой переменной . Результат измерения может рассматриваться как нормально распределённая случайная величина с математическим ожиданием
и соответствующим среднеквадратичным отклонением , характеризующим ошибку измерений. Дополнительно предположим, что «точность измерения во всех точках одинакова, то есть
Тогда плотность вероятности с.в. имеет вид(36)
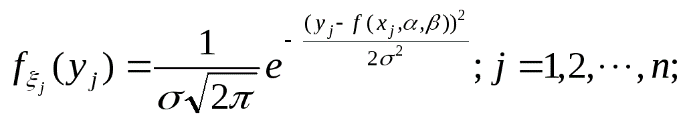
В результате получаем мерную случайную величину
, координаты которой независимы и плотности вероятности которых определении равенствами (36). Как было показано ранее, плотность распределения системы независимых случайных величин равна произведению плотностей вероятности компонент:(37)
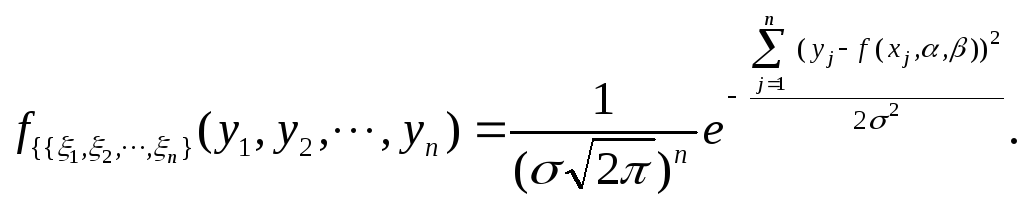
Теперь для определения параметров и воспользуемся идеей метода максимального правдоподобия (ММП), согласно которой в эксперименте реализуются те значения компонент, при которых плотность вероятности системы (37), близка к максимальному значению. Учитывая специальный вид равенств (37), можно заметить, что она достигает максимума, когда показатель степени принимает максимальное значения. Отбрасывая отрицательный множитель
приходим к задаче отыскания минимума выражения:(38)
.Поскольку минимизируется сумма квадратов разностей экспериментальных и теоретических значений функции (их обычно называют «невязками»), предложенную процедуру называют методом наименьших квадратов.
Согласно теории дифференциального исчисления в принципе задача сводится к решению
системы двух однородных дифференциальных уравнений в частных производных:
(39)
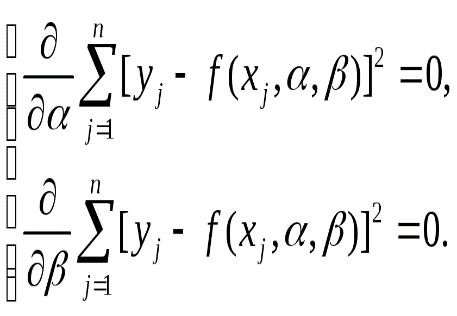
Если функциональная зависимость (35) линейна относительно параметров и , то система уравнений (39) также будет линейной и её решение можно найти известными методами линейной алгебры.
Таким образом, в общем случае мы приходим к следующему выводу.
Метод нахождения оценки
неизвестного параметра , основанный на минимизации суммы квадратов отклонений выборочных данных от определяемой (искомой) оценки называется методом наименьших квадратов.Другими словами, в МНК требуется найти такое значение
, которое минимизировало бы сумму
33. Распределение выборочных характеристик. Распределение выборочного среднего при неизвестной и известной дисперсии. Распределение выборочной дисперсии.
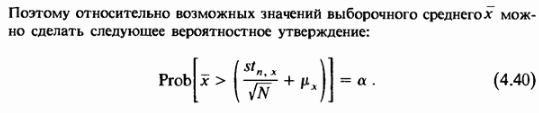
4.3.1. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНОГО СРЕДНЕГО ПРИ ИЗВЕСТНОЙ ДИСПЕРСИИ
Рассмотрим выборочное среднее выборки из N независимых наблюдений случайной величины х:
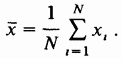
Cреднее значение выборочного распределения величины х равно
Дисперсия выборочного распределения величины х есть
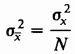
Следовательно, в силу распределения обеих частей следующего соотношения, содержащего х, совпадают:
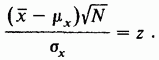
Поэтому относительно возможных значений выборочного среднего можно утверждать, что
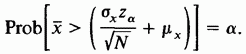
34. Интервальные оценки. Доверительный интервал, доверительная вероятность.
Интервальной называют оценку, которая определяется двумя числами – началом и концом интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть — это оценка неизвестного оцениваемого параметра . Пусть — это некоторое положительное число. Если выполняется неравенство
,то говорят, что интервал 
покрывает неизвестный параметр .Доверительным интервалом называют найденный по данным выборки интервал
, который покрывает неизвестный параметр с заданной надежностью . Надежность задается по условию задачи и обычно принимается равной 0,95, или 0,99, или 0,999.Вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надежными (достоверными), называют доверительной вероятностью или надежностью. Величина доверительной вероятности определяется характером производимых измерений. При выполнении учебных лабораторных работ в курсе общей физики доверительная вероятность обычно считается равной 95 %.
35. Вариационный ряд. Таблица частот. Гистограмма.
Вариационный ряд — это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака. Например, больных по возрасту, по срокам лечения, новорожденных по весу и т.п.
Наиболее естественной формой эмпирического закона распределения является так называемая таблица частот (относительных частот), в первой строке которой записываются числа вариационного ряда, а во второй –– соответствующие им частоты n і (относительные частоты w і). Сумма всех частот равна объему выборки п, а сумма всех относительных частот равна единице.
Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которой служат частичные интервалы длины h, а высоты равны nj.
Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высотами – относительные частоты ωj.
36. Проверка статистических гипотез.
Под статистической гипотезой или просто гипотезой понимают всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.
Статистические гипотезы служат инструментом проверки выдвигаемых теоретических предположений. Гипотезы могут быть высказаны относительно параметров статистического распределения вероятностей. Например, в случае нормального закона распределения с.в., относительно м.о. и дисперсии. Тогда гипотезу называют параметрической.
Предположения могут быть сделаны так же относительно самого распределения с.в. (подчинение закону Бернулли, Пуассона, геометрическому, равномерному, нормальному и т.д.). В этом случае проверяемую гипотезу называют непараметрической.
На практике одну из гипотез выделяют в качестве основной или нулевой и обозначают
, (которая формируется в предположении отсутствия существенной различии между выборочной и генеральной совокупностями), а другую конкурирующей гипотезы, являющуюся противоположной к , т.е. логическим отрицанием первого