ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 143
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, в качестве альтернативной гипотезы и обозначается.
Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой, если в ней идёт речь об одном значении параметра, в противном случае –сложной.
Например, гипотеза , состоящая в том, что математическое ожидание с.в. равно , то есть
, состоящая в том, что математическое ожидание с.в. равно , то есть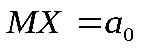 , является простой. В качестве альтернативной гипотезы, т.е. сложной можно рассматривать одну из следующих гипотез:
, является простой. В качестве альтернативной гипотезы, т.е. сложной можно рассматривать одну из следующих гипотез: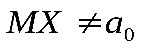 или
или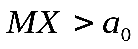 ,
,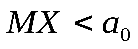 .
.
Имея две гипотезы и надо на основе выборки
и надо на основе выборки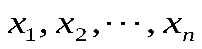 , принять либо основную гипотезу
, принять либо основную гипотезу , либо конкурирующую . Исследуя выборку, принимается решение: согласуется она с этой гипотезой или нет. Альтернативная гипотеза принимается после того, как опровергается основная (нулевая).
, либо конкурирующую . Исследуя выборку, принимается решение: согласуется она с этой гипотезой или нет. Альтернативная гипотеза принимается после того, как опровергается основная (нулевая).
Правило, по которому принимается решение принять или отклонить гипотезу , или отклонить или принять , называется статистическим критерием или просто критерием проверки данной гипотезы.
, или отклонить или принять , называется статистическим критерием или просто критерием проверки данной гипотезы.
Проверку гипотез осуществляют на основании результатов выборки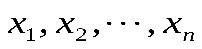 , из некоторых формируют функцию выборки
, из некоторых формируют функцию выборки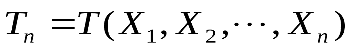 , называемой статистикой критерия.
, называемой статистикой критерия.
Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия разбивается на два непересекающихся подмножества:
критическую область т.е. область отклонения гипотезы и область принятия гипотезы
и область принятия гипотезы  . Если фактически наблюдаемое значение статистики критерия, т.е. значение критерия, вычисленное по выборке:
. Если фактически наблюдаемое значение статистики критерия, т.е. значение критерия, вычисленное по выборке: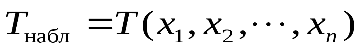 попадает в критическую область то основная гипотеза
попадает в критическую область то основная гипотеза отклоняется и принимается альтернативная гипотеза ; если же
отклоняется и принимается альтернативная гипотеза ; если же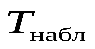 попадает в область , то принимается
попадает в область , то принимается , а отклоняется.
, а отклоняется.
37. Проверка гипотезы о равенстве средних двух нормальных распределений с известными и неизвестными дисперсиями
Пусть X и Y – нормальные генеральные совокупности с известными генеральными дисперсиями σx2 и σy2 и неизвестными математическими ожиданиями μx и μy . Из генеральных совокупностей взяты две независимые выборки объёмами nx и ny и вычислены выборочные средние арифметические и . Для проверки гипотезы о равенстве генеральных средних H0: μx = μy используют статистический критерий: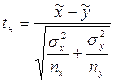 , который при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения N(0;1).
, который при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения N(0;1).
Выбор критической области зависит от содержания конкурирующей гипотезы H1. Согласно требованию к критической области при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.
Границы критических областей при заданном уровне значимости α находят по интегральной функции Лапласа из условия Ф(tкр
) = 1 – 2α (для правосторонней и левосторонней критических областей) и условия Ф(tкр) = 1 – α (для двусторонней критической области).
Проверка гипотезы сводится к следующему: если |tн| > tкр, нулевая гипотеза H0 отвергается с вероятностью ошибки α, если |tн| ≤ tкр, то делается вывод, что нулевая гипотеза не противоречит опытным данным.
При неизвестных генеральных дисперсиях либо требуется достаточно большой объём выборки для надёжной и точной оценки, либо требуется, чтобы эти дисперсии были одинаковы (σx2 = σy2), в противном случае известные критерии малоэффективны.
Если из двух генеральных совокупностей взяты две случайные независимые выборки со средними значениями , и выборочными дисперсиями Sx2, Sy2, то для проверки гипотезы H0: μx = μy используют статистику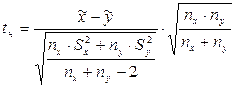 , имеющую распределение Стьюдента с k = nx + ny – 2 степенями свободы. Вид критической области зависит, как обычно, от конкурирующей гипотезы: при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.
, имеющую распределение Стьюдента с k = nx + ny – 2 степенями свободы. Вид критической области зависит, как обычно, от конкурирующей гипотезы: при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.
Границы критической области (tкр) находят по таблице распределения Стьюдента при двусторонней симметричной критической области для заданного уровня значимости α, а при правосторонней и левосторонней критических областях при 2α и числе степеней свободы k = nx + ny – 2.
Правила проверки гипотезы H0: μx = μy такие же, как у гипотезы H0: μ = μ0. Гипотеза H0 отвергается при |tн| > tкр.
38. Двухвыборочный t-тест с одинаковыми и различными дисперсиями.
На основе t-теста строится процедура проверки гипотез о равенстве средних (математических ожиданий) двух независимых нормальных распределений с неизвестными дисперсиями и.
Относительно дисперсий и можно выдвинуть следующие два предположения:
В случае когда обе дисперсии неизвестны, но предполагается что они равны между собой, мы имеем дело с двумя оценками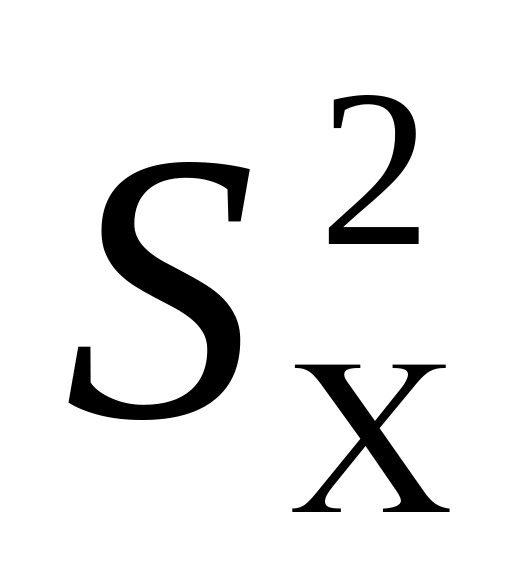 и
и 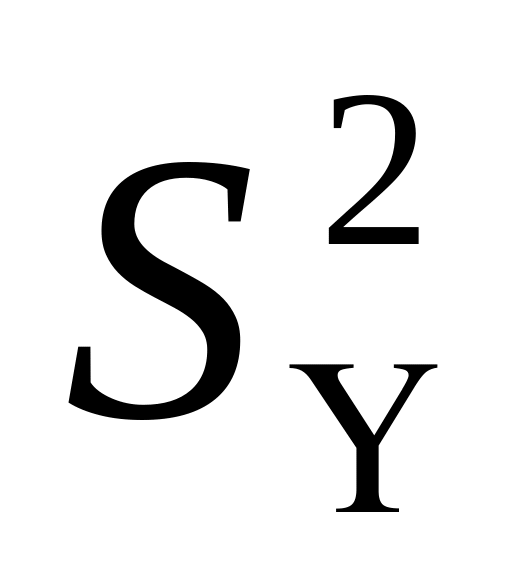 одной и той же дисперсии = . в этом случае строится объединённая оценка :
одной и той же дисперсии = . в этом случае строится объединённая оценка :
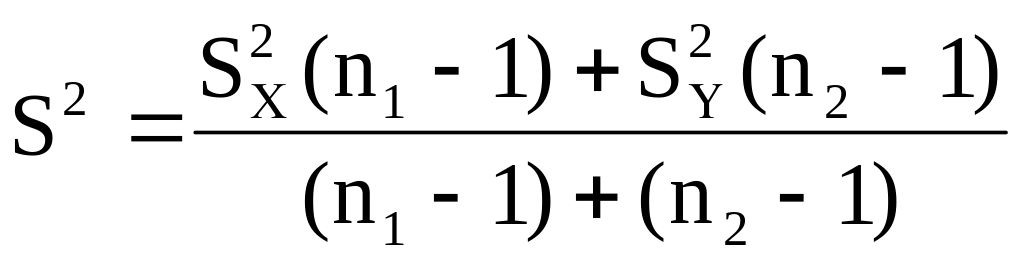 ,
,
S2- это объединённая оценка дисперсии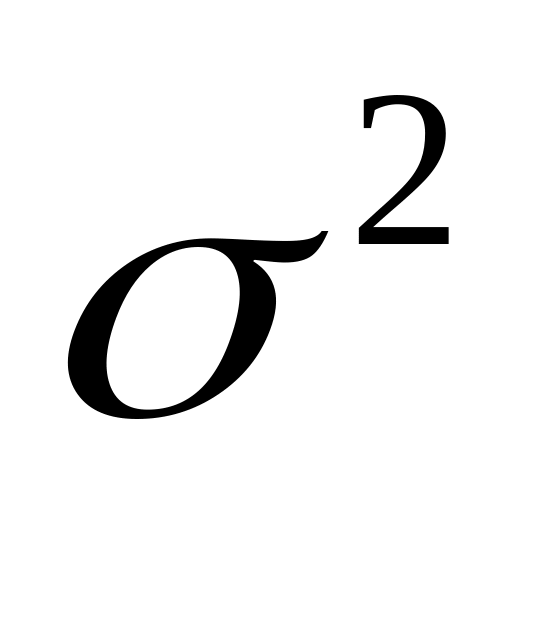 = = .
= = .
В математической статистике доказывается, что если нулевая гипотеза о равенстве математических ожиданий H0: mx=my выполняется, то величина t вычисляется по формуле:
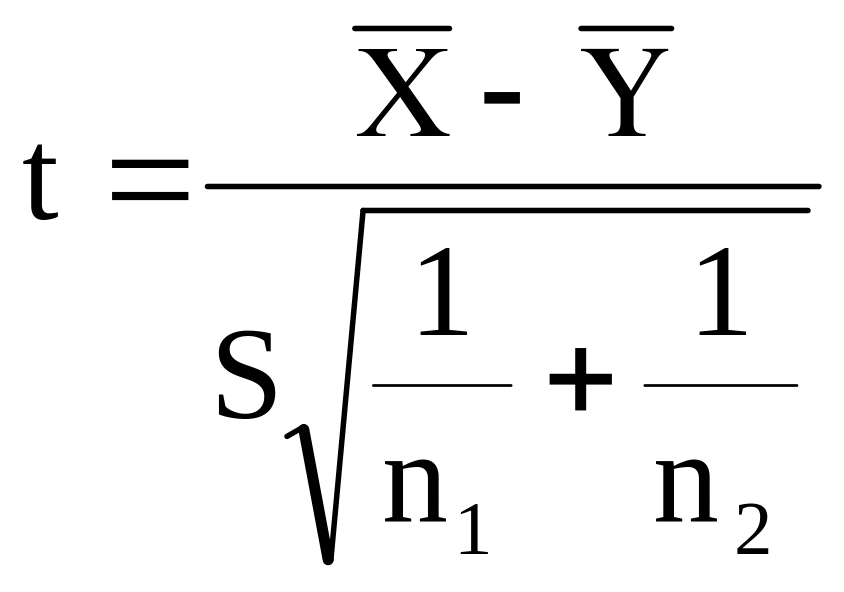
где и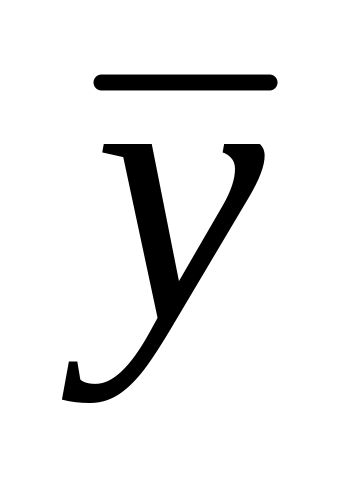 - средние арифметические величины,
- средние арифметические величины,
n1 – число наблюдений в первой выборке,
n2- число наблюдений во второй выборке,
S – выборочное стандартное отклонение,
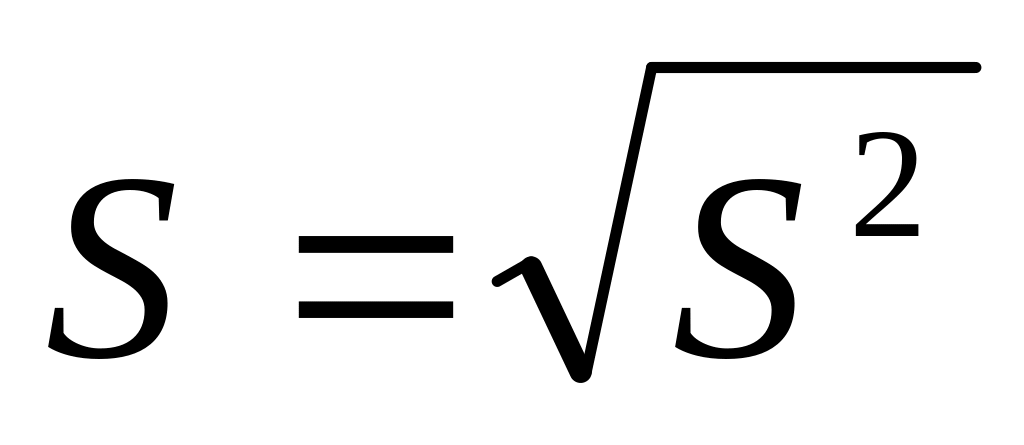 .
.
Статистика t имеет распределение Стьюдента. Число степеней свободы определяется по формуле:
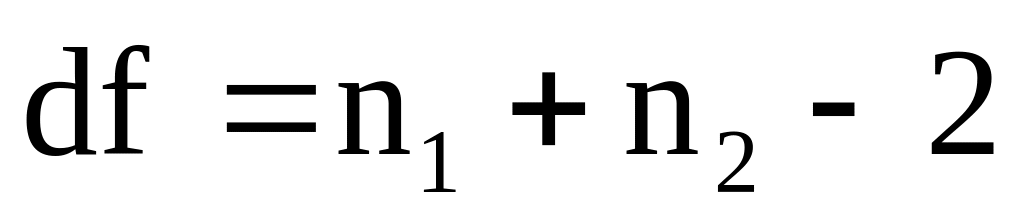
Эту t-статистику и используют в качестве критерия при проверке нулевой гипотезы о равенстве математических ожиданий. Схема проверки аналогична проверке при использовании Z-теста.
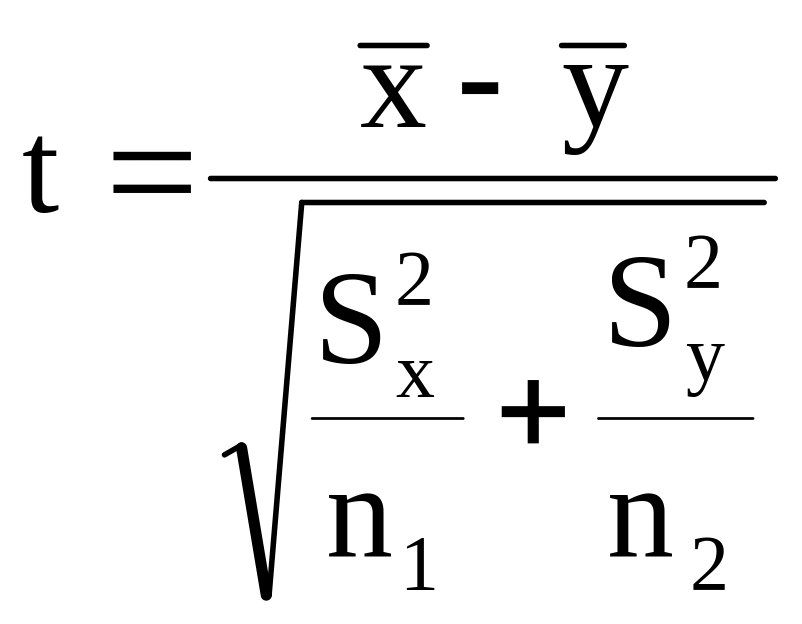 — это распределение близко распределению Стьюдента. Число степеней свободы вычисляется по следующей формуле:
— это распределение близко распределению Стьюдента. Число степеней свободы вычисляется по следующей формуле:
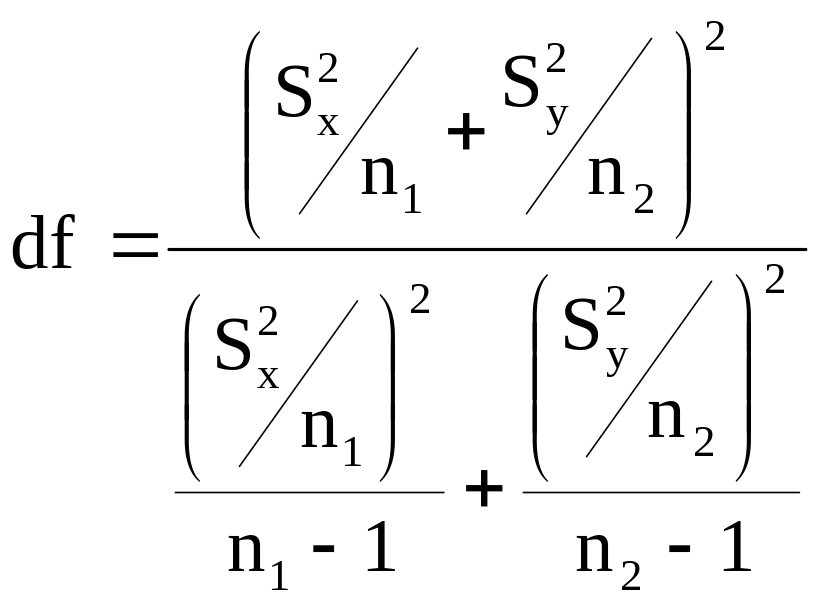
В данном случае t-статистику, используемую для проверки нулевой гипотезы о равенстве средних величин при различных неизвестных дисперсиях, называют критерием
Фишера-Беренса.
Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой, если в ней идёт речь об одном значении параметра, в противном случае –сложной.
Например, гипотеза
Имея две гипотезы
Правило, по которому принимается решение принять или отклонить гипотезу
Проверку гипотез осуществляют на основании результатов выборки
Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия разбивается на два непересекающихся подмножества:
критическую область т.е. область отклонения гипотезы
37. Проверка гипотезы о равенстве средних двух нормальных распределений с известными и неизвестными дисперсиями
Пусть X и Y – нормальные генеральные совокупности с известными генеральными дисперсиями σx2 и σy2 и неизвестными математическими ожиданиями μx и μy . Из генеральных совокупностей взяты две независимые выборки объёмами nx и ny и вычислены выборочные средние арифметические и . Для проверки гипотезы о равенстве генеральных средних H0: μx = μy используют статистический критерий:
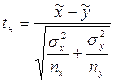 , который при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения N(0;1).
, который при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения N(0;1).Выбор критической области зависит от содержания конкурирующей гипотезы H1. Согласно требованию к критической области при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.
Границы критических областей при заданном уровне значимости α находят по интегральной функции Лапласа из условия Ф(tкр
) = 1 – 2α (для правосторонней и левосторонней критических областей) и условия Ф(tкр) = 1 – α (для двусторонней критической области).
Проверка гипотезы сводится к следующему: если |tн| > tкр, нулевая гипотеза H0 отвергается с вероятностью ошибки α, если |tн| ≤ tкр, то делается вывод, что нулевая гипотеза не противоречит опытным данным.
При неизвестных генеральных дисперсиях либо требуется достаточно большой объём выборки для надёжной и точной оценки, либо требуется, чтобы эти дисперсии были одинаковы (σx2 = σy2), в противном случае известные критерии малоэффективны.
Если из двух генеральных совокупностей взяты две случайные независимые выборки со средними значениями , и выборочными дисперсиями Sx2, Sy2, то для проверки гипотезы H0: μx = μy используют статистику
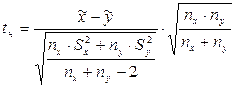 , имеющую распределение Стьюдента с k = nx + ny – 2 степенями свободы. Вид критической области зависит, как обычно, от конкурирующей гипотезы: при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.
, имеющую распределение Стьюдента с k = nx + ny – 2 степенями свободы. Вид критической области зависит, как обычно, от конкурирующей гипотезы: при H1: μx > μy выбирают правостороннюю, при H1: μx < μy – левостороннюю, а при H1: μx ≠ μy – двустороннюю критические области.Границы критической области (tкр) находят по таблице распределения Стьюдента при двусторонней симметричной критической области для заданного уровня значимости α, а при правосторонней и левосторонней критических областях при 2α и числе степеней свободы k = nx + ny – 2.
Правила проверки гипотезы H0: μx = μy такие же, как у гипотезы H0: μ = μ0. Гипотеза H0 отвергается при |tн| > tкр.
38. Двухвыборочный t-тест с одинаковыми и различными дисперсиями.
На основе t-теста строится процедура проверки гипотез о равенстве средних (математических ожиданий) двух независимых нормальных распределений с неизвестными дисперсиями и.
Относительно дисперсий и можно выдвинуть следующие два предположения:
-
Обе дисперсии неизвестны, но предполагается, что они равны между собой, т.е. = . -
Обе дисперсии неизвестны и предполагается, что они не равны между собой, т.е. ≠ .
В случае когда обе дисперсии неизвестны, но предполагается что они равны между собой, мы имеем дело с двумя оценками
S2- это объединённая оценка дисперсии
В математической статистике доказывается, что если нулевая гипотеза о равенстве математических ожиданий H0: mx=my выполняется, то величина t вычисляется по формуле:
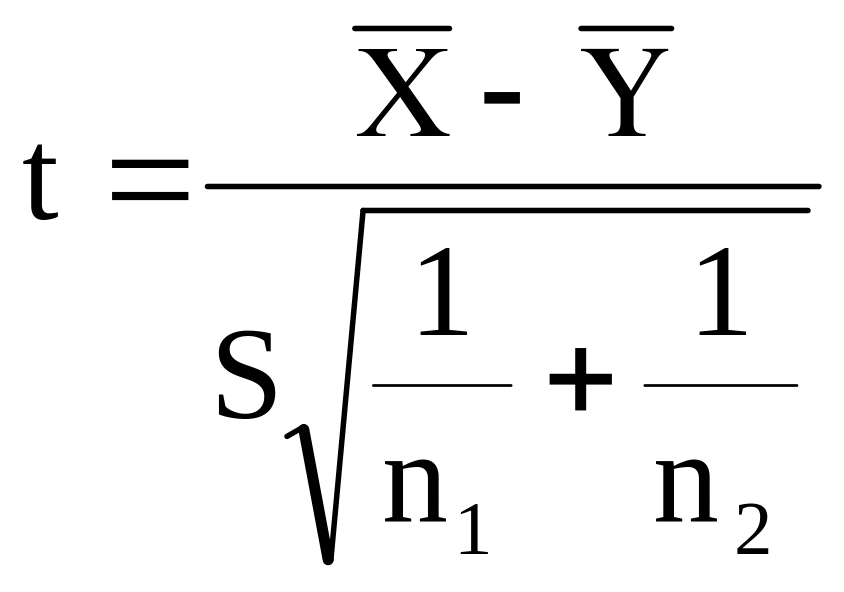
где и
n1 – число наблюдений в первой выборке,
n2- число наблюдений во второй выборке,
S – выборочное стандартное отклонение,
Статистика t имеет распределение Стьюдента. Число степеней свободы определяется по формуле:
Эту t-статистику и используют в качестве критерия при проверке нулевой гипотезы о равенстве математических ожиданий. Схема проверки аналогична проверке при использовании Z-теста.
-
В случае, когда дисперсии неизвестны и предполагается, что они не равны, используется аналог Z-теста с заменой дисперсий их оценками.
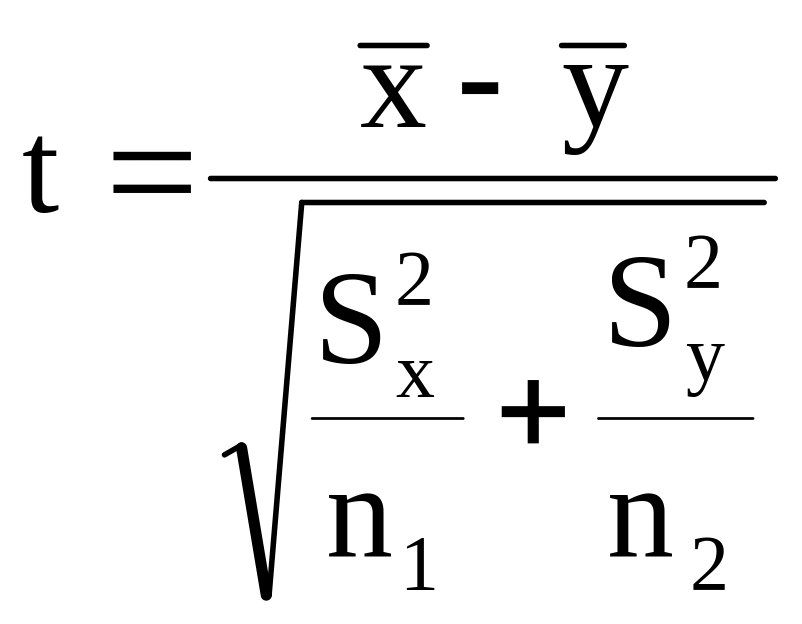 — это распределение близко распределению Стьюдента. Число степеней свободы вычисляется по следующей формуле:
— это распределение близко распределению Стьюдента. Число степеней свободы вычисляется по следующей формуле: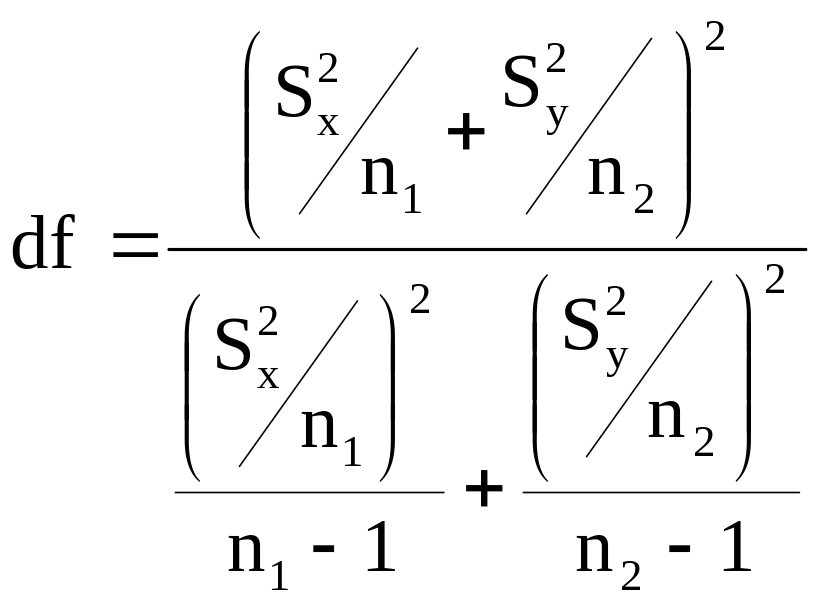
В данном случае t-статистику, используемую для проверки нулевой гипотезы о равенстве средних величин при различных неизвестных дисперсиях, называют критерием
Фишера-Беренса.