ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 144
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- среднее число наблюдений в каждой градации фактора B.
Дисперсии вычисляются следующим образом:
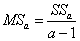- дисперсия, объяснённая влиянием фактора A,
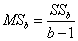- дисперсия, объяснённая влиянием фактора B,
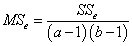- необъяснённая дисперсия или дисперсия ошибки,
где
va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,
vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,
ve = (a − 1)(b − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = ab − 1 - общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:
для фактора A:
H0: μ1A = μ2A = ... = μaA,
H1: не все μiA равны;
для фактора B:
H0: μ1B = μ2B = ... = μaB,
H1: не все μiB равны.
Чтобы определить влияние фактора A, нужно фактическое отношение Фишера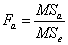
сравнить с критическим отношением Фишера .
Чтобы определить влияние фактора B, нужно фактическое отношение Фишера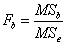
сравнить с критическим отношением Фишера .
Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P
= 1 − α.
Двухфакторный дисперсионный анализ с повторениями:
Двухфакторный дисперсионный анализ с повторениями применяется для того, чтобы проверить не только возможную зависимость результативного признака от двух факторов - A и B, но и возможное взаимодействие факторов A и B. Тогда a - число градаций фактора A и b - число градаций фактора B, r - число повторений. В статистическом комплексе сумма квадратов остатков разделяется на четыре компоненты:
SS = SSa + SSb + SSab + SSe,
где
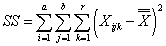- общая сумма квадратов отклонений,
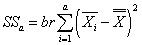- объяснённая влиянием фактора A сумма квадратов отклонений,
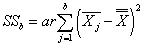- объяснённая влиянием фактора B сумма квадратов отклонений,
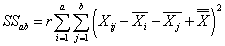- объяснённая влиянием взаимодействия факторов A и B сумма квадратов отклонений,
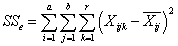- необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки,
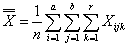- общее среднее наблюдений,
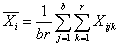- среднее наблюдений в каждой градации фактора A,
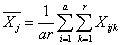- среднее число наблюдений в каждой градации фактора B,
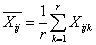- среднее число наблюдений в каждой комбинации градаций факторов A и B,
n = abr - общее число наблюдений.
Дисперсии вычисляются следующим образом:
- дисперсия, объяснённая влиянием фактора
A,
- дисперсия, объяснённая влиянием фактора B,
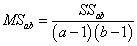- дисперсия, объяснённая взаимодействием факторов A и B,
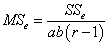- необъяснённая дисперсия или дисперсия ошибки,
где
va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,
vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,
vab = (a − 1)(b − 1) - число степеней свободы дисперсии, объяснённой взаимодействием факторов A и B,
ve = ab(r − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = abr − 1 - общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются три нулевые гипотезы и соответствующие альтернативные гипотезы:
для фактора A:
H0: μ1A = μ2A = ... = μaA,
H1: не все μiA равны;
для фактора B:
H0: μ1B = μ2B = ... = μaB,
H1: не все μiB равны;
для взаимодействия факторов A и B:
H0: ABij = 0,
H1: ABij ≠ 0 для всех i и j.
Чтобы определить влияние фактора A, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .
Чтобы определить влияние фактора B, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .
Чтобы определить влияние взаимодействия факторов A и B, нужно фактическое отношение Фишера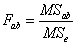
сравнить с критическим отношением Фишера .
Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 −
α.
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.
Дисперсии вычисляются следующим образом:
- дисперсия, объяснённая влиянием фактора A, - дисперсия, объяснённая влиянием фактора B, - необъяснённая дисперсия или дисперсия ошибки,где
va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,
vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,
ve = (a − 1)(b − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = ab − 1 - общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:
для фактора A:
H0: μ1A = μ2A = ... = μaA,
H1: не все μiA равны;
для фактора B:
H0: μ1B = μ2B = ... = μaB,
H1: не все μiB равны.
Чтобы определить влияние фактора A, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .Чтобы определить влияние фактора B, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P
= 1 − α.
Двухфакторный дисперсионный анализ с повторениями:
Двухфакторный дисперсионный анализ с повторениями применяется для того, чтобы проверить не только возможную зависимость результативного признака от двух факторов - A и B, но и возможное взаимодействие факторов A и B. Тогда a - число градаций фактора A и b - число градаций фактора B, r - число повторений. В статистическом комплексе сумма квадратов остатков разделяется на четыре компоненты:
SS = SSa + SSb + SSab + SSe,
где
- общая сумма квадратов отклонений, - объяснённая влиянием фактора A сумма квадратов отклонений, - объяснённая влиянием фактора B сумма квадратов отклонений, - объяснённая влиянием взаимодействия факторов A и B сумма квадратов отклонений, - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки, - общее среднее наблюдений, - среднее наблюдений в каждой градации фактора A, - среднее число наблюдений в каждой градации фактора B, - среднее число наблюдений в каждой комбинации градаций факторов A и B,n = abr - общее число наблюдений.
Дисперсии вычисляются следующим образом:
- дисперсия, объяснённая влиянием фактора
A,
- дисперсия, объяснённая влиянием фактора B, - дисперсия, объяснённая взаимодействием факторов A и B, - необъяснённая дисперсия или дисперсия ошибки,где
va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,
vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,
vab = (a − 1)(b − 1) - число степеней свободы дисперсии, объяснённой взаимодействием факторов A и B,
ve = ab(r − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = abr − 1 - общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются три нулевые гипотезы и соответствующие альтернативные гипотезы:
для фактора A:
H0: μ1A = μ2A = ... = μaA,
H1: не все μiA равны;
для фактора B:
H0: μ1B = μ2B = ... = μaB,
H1: не все μiB равны;
для взаимодействия факторов A и B:
H0: ABij = 0,
H1: ABij ≠ 0 для всех i и j.
Чтобы определить влияние фактора A, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .Чтобы определить влияние фактора B, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .Чтобы определить влияние взаимодействия факторов A и B, нужно фактическое отношение Фишера
сравнить с критическим отношением Фишера .Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 −
α.
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.