Файл: Уроковконсультаций в 11 классе. Задачи с параметром.docx

Скачать файл (0,08Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 17

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

m > 1;

Ответ: m

; -3)

6.Рассмотрим задачи на установления числа корней уравнения.

При каких значениях а уравнение

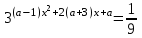имеет единственный корень?

Решение. В силу свойств показательной функции данное показательное уравнение равносильно уравнению

(а-1)х² +2(а+3)х + а = -2,

т.е. исходное уравнение имеет единственный корень тогда и только тогда, когда уравнение

(а-1)х² +2(а+3)х + а +2 = 0; имеет единственный корень.

При а=1 имеем

;

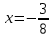При а ≠ 1 квадратное уравнение имеет один корень если Д=0. Д= 5а + 11 ; а=-2.2

Итак, исходное показательное уравнение имеет один корень только при а = 1 и

при а = -2,2

Ответ: а=-2,2, а=1.
Пример 1. При каких значениях параметра, а уравнение 2 cos²x – (2а + 9)cosx + 9а = 0 не имеет корней.

Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у² – (2 а + 9)у + 9а = 0, корни которого у₁ = а, у₂ = 4,5.

Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если

> 1.

Ответ: (-

; -1)

(1;

).

Задачи на нахождение общего корня двух уравнений.

Пример 1. При каких значениях параметра а уравнение х² + 3х + 7а -21 =0 и х

² +6х +5а -6 =0 имеют общий корень?

Решение. Исключим параметр а из полученной системы.

Для этого первое уравнение умножим на (-5), второе умножим на7, а результаты сложим.

Получим: 2х² + 27х +63 =0, корни которого х₁ = -3, х₂ = -10,5.

Подставим корни в одно из уравнений и найдем значение параметра а.

Ответ: 3 и – 8,25.

Пример 2. При каких значениях параметра а уравнение х² – ах + 2 = 0 и 3х² + (а - 9)х+ 3=0 равносильны?

Решение. Как известно уравнения равносильны, если множество их корней совпадают. Рассмотрим 2 случая.

1) Уравнения не имеют корней (множество корней пусто). Тогда их дискриминанты отрицательны:

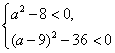
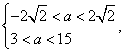
Система неравенств решений не имеет.

2) Уравнения имеют общие корни. Тогда

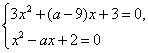
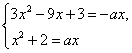
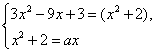
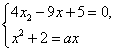
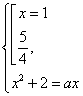
Следовательно, данные уравнения могут иметь общие корни только приа = 3 или а =

.

Проверить самостоятельно!

7.Задачи с применением геометрической интерпретации.

Решение задач с параметрами может существенно облегчить использование графиков.

Пример 1. Укажите количество корней в зависимости от параметра а:

.

Решение.

Построим график функции а =

.
Количество корней можно увидеть на рисунке:

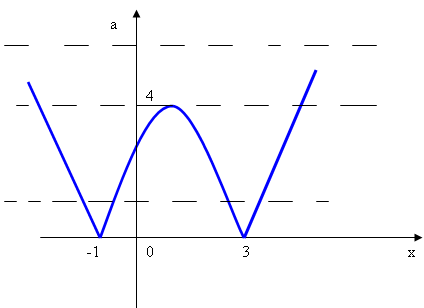
Ответ: 1) еслиа < 0, то корней нет;

2) еслиа = 0,а > 4, то 2 корня

3) если 0 < a < 4, то 4 корня.

4) еслиа = 4, то 3 корня

8.Рефлексия. Итог урока. Оценки.

Самостоятельную работу можно предложить учащимся в классе, как и в качестве дополнительной работы по теме на последующих уроках…

Спасибо за урок!

Реши самостоятельно1 вариант	Реши самостоятельно2 вариант
1) Решите уравнение: 0 · х = а	1) Решить уравнение: а х = а.
2) Решит уравнение: (в – 2)·х = 5 + в.	2) Решите уравнение (в + 1)·х = 3 – в.
3) При каких значениях параметра с уравнение имеет бесконечное множество решений? с·(с + 1)·х = с² – 1.	3) При каких значениях параметра с уравнение имеет бесконечное множество решений? (с² – 4)·х = (с – 2)·(с+ 1).
4) При каких значениях параметра m уравнения не имеет решений? .	4) При каких значениях параметра m уравнения не имеет решений? .
5) Решить уравнение .	5) Решить уравнение .
6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (5 – n) = 0.	6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (3 + n) = 0

Реши самостоятельно1 вариант	Реши самостоятельно2 вариант
1) Решите уравнение: 0 · х = а	1) Решить уравнение: а х = а.
2) Решит уравнение: (в – 2)·х = 5 + в.	2) Решите уравнение (в + 1)·х = 3 – в.
3) При каких значениях параметра с уравнение имеет бесконечное множество решений? с·(с + 1)·х = с² – 1.	3) При каких значениях параметра с уравнение имеет бесконечное множество решений? (с² – 4)·х = (с – 2)·(с+ 1).
4) При каких значениях параметра m уравнения не имеет решений? .	4) При каких значениях параметра m уравнения не имеет решений? .
5) Решить уравнение .	5) Решить уравнение .
6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (5 – n) = 0.	6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (3 + n) = 0

ОТВЕТЫ

1 вариант	2 вариант
1) Решите уравнение: 0 · х = а Ответы: при а = 0, х R, при а ≠ 0 корней нет	1) Решить уравнение: а х = а. Ответы: при а ≠ 0, х = 1, при а = 0, х R
2) Решит уравнение: (в – 2)·х = 5 + в. Ответы: при в = 2 нет корней; при в ≠2, х = ;	2) Решите уравнение (в + 1)·х = 3 – в. Ответы: при в = -1 нет корней, при в ≠ - 1
3) При каких значениях параметра с уравнение имеет бесконечное множество решений? с·(с + 1)·х = с² – 1. Ответ: при с = -1, х R	3) При каких значениях параметра с уравнение имеет бесконечное множество решений? (с² – 4)·х = (с – 2)·(с+ 1). Ответ: при с = 2, х R
4) При каких значениях параметра m уравнения не имеет решений? . Ответы: при m = 7 нет корней;	4) При каких значениях параметра m уравнения не имеет решений? . Ответы: при m = 8 нет корней.
5) Решить уравнение . Ответы:при а = 0 нет корней, при а ≠ 0 х = 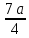;	5) Решить уравнение . Ответы:при а = 0 нет корней, при а ≠ 0 х = ;
6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (5 – n) = 0. Ответы: при n= 0, х = - ; при n = 1, х = - 2;при n =4,х = - .	6) При каких значениях параметра n уравнение имеет один корень? nх² + 4х + (3 + n) = 0. Ответы: при n = 0, х = - ; при n = 1, х = 2;при n = - 4, х = ;