Файл: Методические указания по выполнению контрольной работы по дисциплине статистика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 85
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «СТАТИСТИКА»
Введение
Статистика является общественной наукой, которая изучает явления и процессы общественной жизни в их количественно-качественной определенности. Она разрабатывает общие положения и методы статистического исследования. Ее категориями, показателями и методами пользуются все другие отрасли статистической науки. В результате изучения студенты овладевают знаниями общих основ статистической науки и общими навыками проведения статистического исследования, изучают методология сбора, обработки и анализа статистической информации.
В соответствии с учебным планом студенты заочной формы обучения специальностей «Государственное и муниципальное управление», «Связи с общественностью», «Реклама» и «Политология» выполняют контрольную работу по курсу статистика.
Цель контрольной работы – изучить важнейшие методологические вопросы, проверить умение студента применять на практике основные положения курса, приобрести практические навыки в расчетах статистических показателей, научить понимать экономический смысл исчисленных показателей, анализировать их и изображать графически.
1. Требования по оформлению контрольной работы и РГР
Выполненная контрольная работа должна соответствовать следующим требованиям:
− работа должна быть выполнена и представлена на рецензирование в срок, установленный преподавателем;
− задачи следует решать в том порядке, в каком они даны в задании;
− перед решением задачи должно быть полностью приведено ее условие;
− решение задач следует сопровождать необходимыми формулами, подробными расчетами и краткими пояснениями, изображать графически. Произведенные расчеты нужно проверять взаимосвязью между исчисленными показателями. Необходимо четко формулировать выводы, раскрывающие экономическое содержание и значение исчисленных показателей. Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты до 0,1.
Студенты, не получившие зачета по контрольной работе к зачету/экзамену не допускаются. Если выполнение контрольной работы и вызывает затруднения, следует обратиться за консультацией.
2. Указания о порядке выполнения контрольной работы
и ее содержание
Приступить к выполнению контрольной работы следует после проработки теоретического материала.
Контрольная работа по статистике состоит из шести вариантов, в каждом варианте соответственно по 8 задач. Выбор варианта определяется последней цифрой зачетной книжки студента (таблица 1):
Таблица 1
| Последняя цифра зачетной книжки | Номер выполняемого варианта |
| 1, 6 | Первый |
| 2, 7 | Второй |
| 3, 8 | Третий |
| 4, 9 | Четвёртый |
| 5, 10 | Пятый |
Общая теория статистики
Задача 1 составлена на тему «Абсолютные и относительные величины».
Существуют следующие виды относительных величин:
− выполнение договорных обязательств (задания, плана) показывает отношение фактических показателей к договорным или плановым;
− структуры, показывают отношение частей к целому или отношение групп ко всей совокупности;
− динамики или темпы роста, показывают изменение явления во времени, характеризуют рост или снижение каких-либо показателей в сравниваемых периодах. При расчёте темпов роста различают два периода: базисный и отчётный. Относительная величина динамики (темп роста, базисный) – это отношение уровня показателя каждого периода к первоначальному уровню с постоянной базой сравнения. Относительная величина динамики (темп роста, цепной) – это отношение уровня показателя каждого периода к первоначальному уровню с переменной базой сравнения.
− сравнения, сопоставляются уровни одноименных показателей относящиеся к различным объектам наблюдения, взятым за один пи тот же период времени или на один момент времени;
− координации, представляют собой одну из разновидностей показателей сравнения;
− интенсивности, характеризуют степень распространенности или развития того или иного влияния в определенной среде. Чаще всего они 5
выражаются в именованных величинах.
Задачи 2 и 3 составлены по темам «Средние величины» и «Показатели вариации».
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Средние, используемые в статистике, относятся к двум классам: степенные средние и структурные средние. Из первого класса наиболее часто применяются средняя арифметическая и средняя гармоническая. Средняя геометрическая применяется только при исчислении средних показателей рядов динамики, средняя квадратическая – при исчислении показателей вариации. Представителями второго класса средних являются мода и медиана.
Если данные таковы, что в исходном соотношении средней не известен числитель, а известен знаменатель, то данное соотношение приводит к исчислению средней арифметической взвешенной:
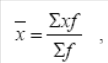
где x – варианты признака; f – частоты.
Если данные таковы, что в исходном соотношении средней известен числитель, а не известен знаменатель, то данное соотношение приводит к исчислению средней гармонической взвешенной:
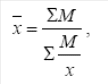
где М – суммарный объем признака в данной группе.
Исследование вариации является составным элементом статистического анализа, позволяющим оценить колебания значений изучаемого признака, однородность совокупности по данному признаку, взаимосвязь его с другими признаками. Показатели вариации служат критерием типичности рассчитанных по совокупности средних величин, используются в определении ошибок выборочных характеристик.
При изучении данной темы необходимо обратить особое внимание на расчет основных показателей вариации:
Размах вариации (R):
R= xmax – xmin,
где xmax, xmin – максимальное и минимальное значение признака соответствено.
Среднее линейное отклонение (d):
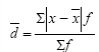– для сгруппированные данных, 
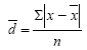– для несгруппированных данных,где n – число вариант
Дисперсия (σ2):
– для сгруппированные данных,
– для несгруппированных данных.Среднее квадратическое отклонение (σ):
Коэффициент вариации:
Задача 4 составлена по теме «Ряды динамики».
Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для ее отражения строятся ряды динамики.
Ознакомившись с литературой и рассмотрев ряды динамики, опубликованные в статистических ежегодниках и справочниках студент должен уяснить, что такое ряд динамики и как он строиться. Особое внимание следует обратить на условия сопоставимости данных, составляющих динамический ряд. При рассмотрении вопросов о видах рядов динамики надо, прежде всего, понять различие между моментными и интервальными рядами. Построение, обработка и анализ этих рядов во многом определяется их особенностями.
Затем следует перейти к изучению методов расчета аналитических показателей рядов динамики.
Рассчитывая аналитические показатели ряда динамики, необходимо правильно выбирать базу для сравнения. Этому вопросу следует уделить особое внимание. Необходимо также разобраться в способах получения средних величин ряда: среднего уровня, среднего абсолютного прироста, среднего темпа роста и прироста. Следует помнить, что способ расчета среднего уровня ряда динамики зависит от его вида. При расчете среднего темпа роста необходимо использовать среднюю геометрическую.
Важнейшие статистические показатели:
− абсолютный прирост (цепной)
Δy=yi-yi-1;
− абсолютный прирост (базисный)
Δy=yi-y0,
где yi- уровень сравниваемого периода; yi-1 – уровень предшествующего периода; y0 – уровень базисного периода;
− темп роста (цепной)
;− темп роста (базисный)
;− темп прироста
Тпр=Тр-100;
− абсолютное значение одного процента прироста
.Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики при равных интервалов применяется средняя арифметическая простая:
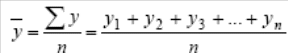,где y – абсолютные уровни ряда;
n – число уровней ряда при неравных интервалах – средняя арифметическая взвешенная:
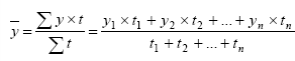
где y1, …, yn – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;
t1, …, tn – веса, длительность интервалов времени между смежными датами.
Средний уровень для моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:
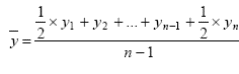,где y1,…, yn – уровни периода, за который делается расчет; n – число уровней периода; n-1 – длительность периода времени
Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной:
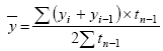
где yI, yn – уровни рядов динамики; t – интервал времени между смежными уровнями.
Средний абсолютный прирост (убыль):
цепным способом расчета:
,где n – число цепных абсолютных приростов (Δyц) в изучаемом периоде базисным способом расчета:
,где m – число уровней ряда динамики в изучаемом периоде, включая базисный
Средний темп роста:
− по цепному способу расчета
,где n – число цепных коэффициентов роста; Кцр1,…, Кцрn – цепные коэффициенты роста.
− по базисному способу расчета
,где m – число уровней ряда динамики в изучаемом периоде, включая базисной.
Средний темп прироста:
Задачи 5 и 6 составлены по теме «Индексы».
Индексы могут быть индивидуальными и сводными. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. Сводные индексы отражают изменение всех элементов сложного явления. Под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию.