Лабораторная работа №4

Тема: Симплексный метод
Цель работы: Решение задач линейного программирования симплексным методом.

Задание:

1. 
   Рассмотреть нахождение максимума линейной функции.
   
2. 
   Рассмотреть нахождение минимума линейной функции.
   
3. 
   Выполнить индивидуальные задания.
   

Методические указания по выполнению работы.
Основным методом решения задач линейного программирования является симплексный метод или симплекс-метод. Решение задачи оформляется в виде симплекс-таблицы. Переход от одной таблицы к другой называется итерацией. Геометрический смысл данного метода заключается в следующем, производим переход из одной вершины многоугольника (многогранника) к другой до тех пор, пока не достигнем оптимальной вершины или докажем неразрешимость задачи.
Нахождение максимума линейной функции
Пример.


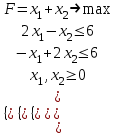
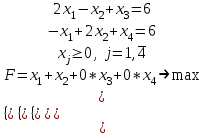
x₃, x₄ – базисные переменные



; ; ; ;

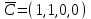
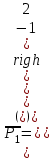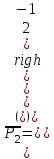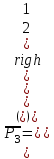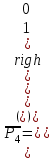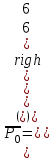
РБ	СБ	Р0	Р1	Р2		Р3		Р4
Р3	0	6	2	-1		1		0
Р4	0	6	-1	2		0		1
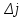		0	-1	-1	0		0

---

Алгоритм метода Последовательное улучшение опорного плана (ПУОП).

Теорема. Критерий оптимальности при F-max

Опорный план Х=(Х₁...Х_n) будет оптимальным, если выполнены следующие условия:

1. 
   P₀≥0
   
2. 
   Dj≥0
   

Ш 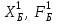аг 1. Из симплекс таблицы определить

Шаг 2.Проверить опорный план на оптимальность согласно теореме. Если план оптимален, то выписать решение. Иначе перейти к шагу 3.

Ш 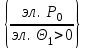аг 3. Выбор разрешающего столбца Q₁

Q₁=max{|Dj<0|}

Шаг 4. Выбор разрешающей строки Q₂=min

Шаг 5. На пересечении Q₁, Q₂ определяем разрешающий элемент и пересчет новой таблицы производим с помощью табличного метода Гаусса. Находим новое опорное решение и возврат к шагу 2.

РБ	СБ	Р0	Р1	Р2		Р3		Р4
Р3	0	6	2	-1		1		0
Р4	0	6	-1	2		0		1
		0	-1	-1	0		0

РБ	СБ	Р0	Р1	Р2		Р3		Р4
Р1	1	3	1		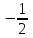		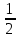	0
Р4	0	9	0		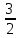		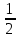	1
		3	0		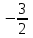		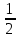0

---

РБ	СБ	Р0	Р1	Р2		Р3		Р4
Р1	1	6	1	0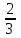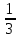
Р2	1	6	0	1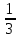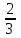
		12	0	0	1		1

Нахождение минимума линейной функции.
Пример.
Перевод минимума F на максимум F по формуле

min F = - max (-F)

min F = -2x₁ – 5x₂  max F = 2x₁ + 5x₂

Применить алгоритм метода ПУОП с изменением шага 3.

Ш 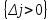аг 3. Q1 = max

Теорема. Критерий оптимальности при F → min

Опорный план х=(х₁...х_n) будет оптимальным, если выполнены условия:

1. 
   P₀≥0
   
2. 
   Dj£0
   

Задания.

Задачи 1 – 8 решить симплексным методом. Сравнить по­лученное решение с решением, найденным геометрически.

1. F = 2х1 - 6х2 → max при ограничениях:	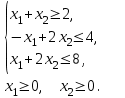2. F = 2х1 - х2 → min при ограничениях: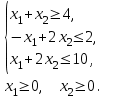
3. F = х1 +х2 → max при ограничениях:	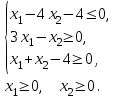4. F = 2х1 - х2 → min при ограничениях: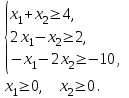

---

5. F = х1 - х2 → max при ограничениях:	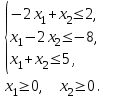6. F =4х1 - 2х2 → max при ограничениях: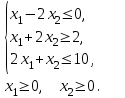
7. 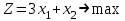при ограничениях:	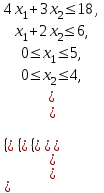8.Z = 3x1 + 2x2max при ограничениях: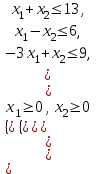

Задачи 9 – 15 решить симплексным методом.


9. F = 2х₁ - 13х₂ - 6х₃ → max при ограничениях:


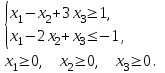
10. F = -6х₁ + 10х₂ + 9х₃ + 8х₄ → min при ограничениях:



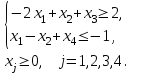
11. F = х₁ + 3х₂ + 2х₃ → min при ограничениях:



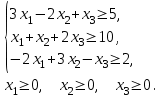
12. F = х₁ + х₂ + х₃ + х₄ → min при ограничениях:


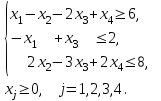
13. F = 4х₁ + 15х₂ + 12х₃ + 2х₄ → min при ограничениях:

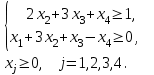ё

14. F = 14х₁ + 10х₂ + 14х₃ + 14х₄ → min при ограничениях:


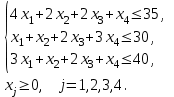
15. F = 3х₁ + 3х₂ - 6х₃ → max при ограничениях:

---

Смотрите также файлы

• Государственная система документационного обеспечения управления.docx

• Задачи привитие умения регулировать напряжение и расслабление своего тела формирование диафрагмальнореберного фонационного речевого дыхания развитие чувства .pptx

• Занятие 2 Преподаватель Таймасханова Эльмира Магомедовна Дисциплина мдк 01. 01. Т е х.docx

• Поражающие факторы современных средств нападения. Защитные сооружения гражданской обороны и их оборудование.docx

• Лабораторная работа 4 Краткое описание Понятие цикла Виды циклов.docx