Министерство образования и науки Российской ФедерацииФедеральное агентство по образованиюГосударственное образовательное учреждение высшего профессионального образованияСАМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТКафедра: Автоматика и управление в технических системахДисциплина: Теория автоматического управленияКурсовая работаСИСТЕМА СТАТИЧЕСКОГО СЛЕЖЕНИЯ ЗА УГЛОВЫМ ПЕРЕМЕЩЕНИЕМВыполнил студент: III – ИТ – 4 Сидоров А. Д.Вариант № 14Проверила: Дилигенская А.Н.Самара 2012Содержание1. Задание на курсовую работу 32. Исходные данные для выполнения курсовой работы 42.2 Исходные данные 42.3 Режимы работы по нагрузке 52.4 Параметры варианта 53. Расчетная часть 63.1 Преобразование структурной схемы 63.2 Определение статического коэффициента передачи K_гр 83.3 Переходный процесс системы до коррекции 83.4. Определение статической ошибки 103.5. Коррекция по ЛАЧХ эквивалентной разомкнутой структуры 103.6. Исследование параметров скорректированной системы 113.7. Функциональная и структурные схемы после коррекции 133.8. Сравнительная таблица показателей переходного процесса 134. Список использованных источников 141 Задание на курсовую работуГлавной задачей является устранение противоречия между требованиями к системе по устойчивости и требованиями по допустимой статической погрешности. Это достигается путем коррекции частотных характеристик разомкнутой системы. Основные этапы выполнения КР:1. Составить структурную схему с входами по задающему воздействию φ_З основному возмущению М_С и выходом по регулируемой координате φ.2. Составить структурную схему с входом φ

---

_З и выходом φ при М_С = 0.3. Составить структурную схему с входом М_С и выходом φ, при φ_З =0.4. Определить статический коэффициент передачи K_гр, обеспечивающий устойчивость структуры и соответствующую ему статическую погрешность в номинальном режиме (2,1.).5. Построить переходные функции по φ_З при K = 0,9K_гр, указать прямые показатели качества этих характеристик.6. Выбором K = K_N и введением корректирующих звеньев обеспечить статическую погрешность в номинальном режиме ε ≤ 0,3ε_гр. Определить схему и выбрать параметры корректирующих звеньев.7. Рассчитать и построить при K = K_N переходную функцию по φ_З, указать ее показатели, в том числе запасы устойчивости по амплитуде и фазе.8. Привести структурную и функциональную схемы после коррекции.9. 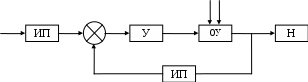Привести сравнительную таблицу показателей переходного процесса до и после коррекции.2 Исходные данные для выполнения курсовой работы2.1 Исходные данныеИсходными материалами КР являются функциональная схема базовой САУ и математические модели звеньев соответствующей структурной (алгоритмической) схемы (Рис.1). M_C J_Н φ_З U_я φ—Рисунок 1 – Функциональная схема САУЗдесь:ОУ – объект управления, состоящий из двигателя постоянного тока (ДПТ) с независимым возбуждением. Влияние собственно нагрузки Н отражается воздействием сопротивления М_С и момента инерции J_Н нагрузки Н на валу двигателя; ИП – измерительный преобразователь; У – усилитель постоянного тока, φ_З – задаваемый угол, φ –обрабатываемый угол.При выполнении курсовой работы используется схема замещения ДПТ (Рис.2), в которой учитывается как обратная связь по скорости K_ω, так и возмущающее воздействие 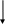М_С. М_СU_я М_В — ω φ—Рисунок 2 – Схема замещения2.2 Режимы работы по нагрузке 2.1 Номинальный режим: М_CN= 0,15∙М_вр.max, J_Н = J_дв

---

2.2 Изменение момента инерции нагрузки, приведенное к валу двигателя2.3 Изменение момента сопротивления, приведенное валу двигателя2.3 Параметры варианта3.1 Требуемые показатели переходной функции φ(t):Перерегулирование σ ≤ 25,0%,Длительность переходного процесса t_П ≤ 1,5 с,Ошибка в установившемся режиме ε_N≤ 0,2 ε_гр, где ε_гр – статическая погрешность в номинальном режиме.3.2 Параметры ДПТ:U_{я max} = 24В,R_я = 0,4 Ом,L_я = 4∙10^-3 = 4∙10^-3 = 15∙10^-3,K_М = 2∙10^-3,K_ω = 0,2 В∙С, J_∑=10^-4 = 10^-4 = 3,74∙10^-4 н∙м∙с²,Здесь N=n₁∙n₂,где n₁ – номер в списке группы – 14,n₂ – номер группы – 1.3.3 Усилитель У и измерительный преобразователь ИП пропорциональные безынерционные звенья.3 Расчетная часть3.1 Преобразование структурной схемыСоставим структурную схему с входами по задающему воздействию φ_З, основному возмущению М_С и выходом по регулируемой координате φ. Для этого используем схему замещения ДПТ, приведенную на рисунке 2, так же воспользуемся тем, что ИП и У являются пропорциональными безынерционными звеньями с передаточными функциями W_ИП = G, W_У = K_У. Приняв значение G=1, звено ИП можно исключить из схемы. Данная схема приведена на рисунке 3:

---

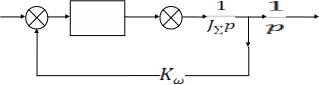
М_С φ_З U_я М_{В —} ωφ— —Рисунок 3 – Структурная схема с входами по задающему воздействию φ_З, основному возмущению М_С и выходом по регулируемой координате φСоставим структурную схему с входом φ_З и выходом φ при М_С = 0 (Рис.4):

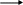
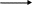
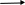
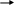
φ_З U_я М_В ω φ — — Рисунок 4 - Структурная схема с входом φ_З и выходом φ при М_С = 0Составим структурную схему со входом по М_С и выходом φ, при φ_З = 0. Для упрощения схемы некоторые звенья будут преобразованы, согласно их соединению, это отражено в передаточных функциях звеньев (Рис.5):

---

М_С ω φ—Рисунок 5 - Структурная схема со входом по М_С и выходом φ, при φ_З = 0Передаточная этой системы:

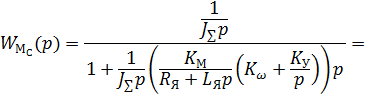(1)

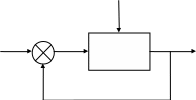
Преобразуем систему, представленную на рисунке 3, к схеме с единичной обратной связью вида (Рис. 6):Мφ_З ε φ—Рисунок 6 – Схема с единичной обратной связьюДля преобразования схемы примем, что М_С = 0. Запишем единую передаточную функцию всей системы:

(2)

Упростим передаточную функцию, раскрыв скобки:

(3)

3.2 Определение статического коэффициента передачи K_грСоставим характеристическое уравнение замкнутой структуры и определим граничное значение коэффициента усилителя K_гр, такое что при K_Угр система устойчива.

Это удобно сделать с помощью критерия Гурвица. Характеристическое уравнение замкнутой системы будет иметь следующий вид:

(4)

Составим матрицу Гурвица:

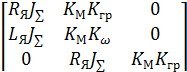(5)

Условие устойчивости по критерию Гурвица::

(6)

Из этого неравенства найдем K_гр:

(7)

Откуда:

(8)

Дальнейший анализ системы до коррекции производится при K_У = 0,9K_гр.
3.3 Переходный процесс системы до коррекции

Построим переходную функцию при М_С = 0, φ_З = const (Рис. 7):



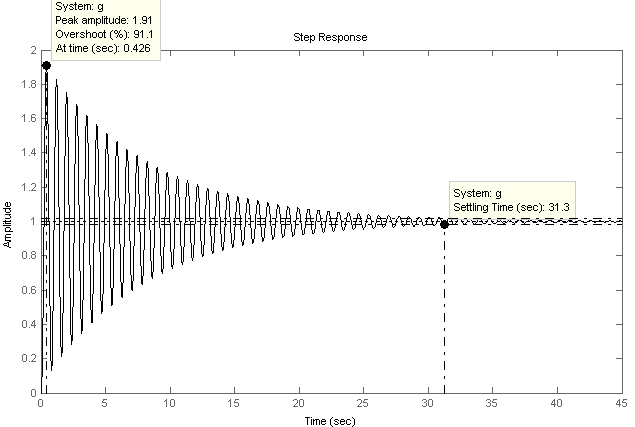
Рисунок 7 – Переходная функция при K_У = 0,9K_гр

Длительность переходного процесса: t_П = 31,3 с;

Перерегулирование: σ% = 91,1%;

Количество перерегулирований: N = 40

Запас устойчивости исходной системы приведены на рисунке 8:



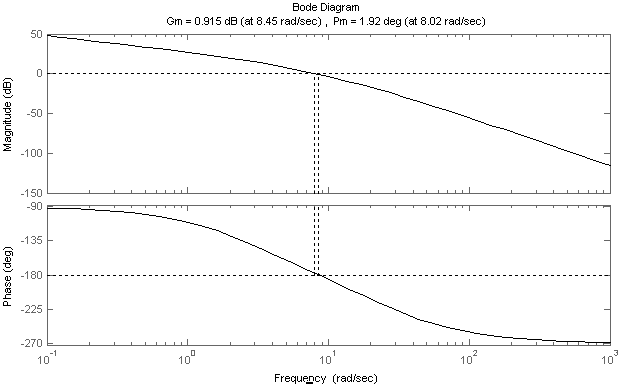
Рисунок 8 –ЛАЧХ и ЛФЧХ

3.4 Определение статической ошибки

Найдем ошибку в установившемся режиме. Воспользуемся тем, что[1]:

(9)

Согласно номинальному режиму, М_CN = 0,15∙М_вр.max

(10)

С учетом φ_з = 1, составим выражение для φ:

	(11)
	(12)

Требуется ε_N ≤ 0,2ε_гр. Для этого:

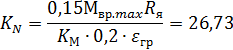(13)

3.5 Коррекция по ЛАЧХ эквивалентной разомкнутой структуры

Найдем корректирующее звено. Для этого построим ЛАЧХ разомкнутой исходной системы и ЛАЧХ желаемой системы:

(14)

Подставив значения, получим:

(15)

Характеристическое уравнение разомкнутой системы:

(16)

Сопрягающие частоты исходной системы: ω₁ = 3с^-1; ω₂ = 23,7с^-1.

Сопрягающая частота, желаемой системы определяется по формуле[1]:

(17)

Где, t_П – время переходного процесса. Согласно требованиям системы t_П=1,5с;

b – коэффициент, связанный с перерегулированием σ. При σ = 25% b = 3;

тогда:

(18)

Частота, ограничивающая со стороны высоких частот:

(19)

Частота, ограничивающая со стороны низких частот:

(20)

Построим ЛАЧХ исходной и желаемой систем (Рис.9):



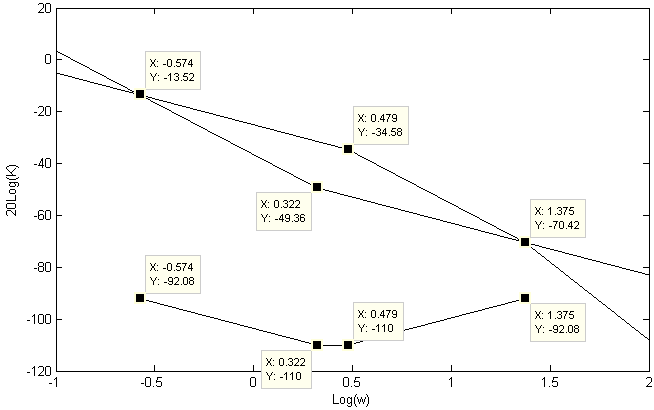
Рисунок 9 – ЛАЧХ

Передаточная функция корректирующего звена[2]:

(21)

Где T₁ = 0,476 c, T₂ = 0, 332 c, T₃ = 3,75 c, T₄ = 0,042 c.

Подставив значения постоянных времени получим:

(22)

3.6 Исследование параметров скорректированной системы

Переходная функция системы с корректирующим звеном приведена на рисунке 10:



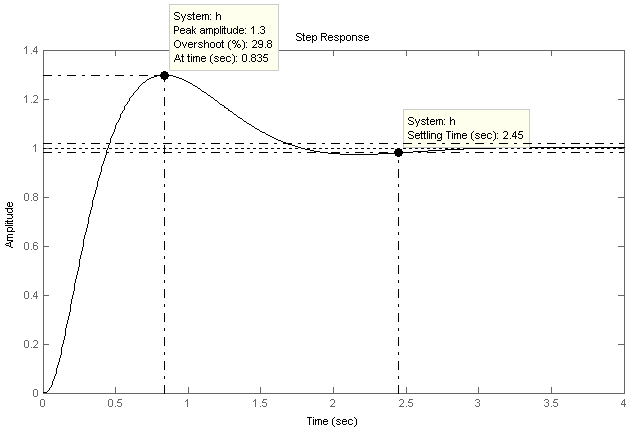
Рисунок 10 – Переходная характеристика скорректированной системы

Длительность переходного процесса: t_П = 2,45 с

Перерегулирование: σ% = 29,8%

ЛАЧХ и ЛФЧХ скорректированной системы представлены на рисунке 11:



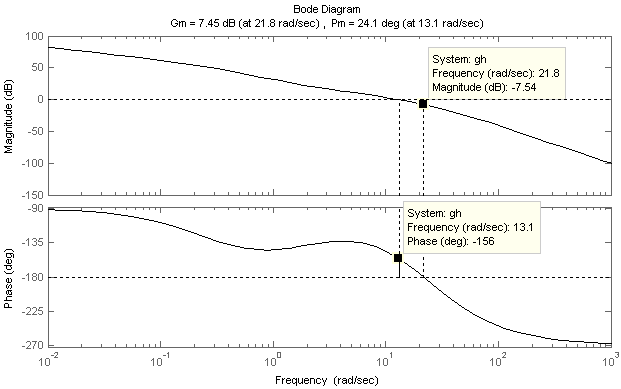
Рисунок 11 – ЛАЧХ и ЛФЧХ

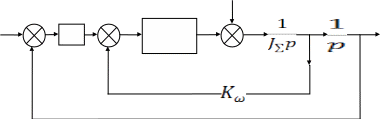
3.7 Функциональная и структурные схемы после коррекции

Ф 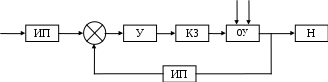ункциональная схема скорректированной системы приведена на рисунке 12:

M_C J_Н

φ_З

—


Рисунок 12 – Функциональная схема скорректированной системы

С 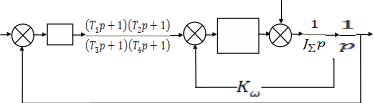труктурная функция скорректированной системы приведена на рисунке 13:

—



— —

Рисунок 13 – Структурная схема скорректированной системы
3.8 Сравнительная таблица показателей переходного процесса

Показатели переходного процесса представлены в сравнительной таблице 1:

Таблица 1 – Показатели переходного процесса

	До коррекции	После коррекции
Длительность переходного процесса, tП	31,3 с	2,45 с
Перерегулирование, σ%	91,1%	29,8%

Требуемые показатели переходного процесса не были достигнуты ввиду исходных данных варианта. Показатели системы улучшились на следующие величины:

Длительность переходного процесса сократилась на 28,85 с.

Перерегулирование уменьшилось на 61,3%.

4 Список использованных источников

1. Методическое пособие по выполнению курсовой работы по курсу ТАУ: метод. пособ к курсовой работе – Самара: самар, техн, ун–т, 16 с.

2. Лысов В. Е. Теория автоматического управления: учебное пособие – Самара: самар, гос. техн, ун–т, 209. 454 с.

---

Смотрите также файлы

• Таырыбы араанды медицина университеті 15ші курс студенттері арасында электронды жне арапайым темекілерді ттынуды жоарлауы.pptx

• Задача 10 Список литературы 11.docx

• Практическая работа к теме 1 Ценности и их роль для человека и общества Изучите контент (информацию).docx

• Тест "Оказание первой помощи" 1 вариант Признаки артериального кровотечения.docx

• Еуразия техникоэкономикалы колледжі курсты Жмыс пн Операциялы жйені жаарту жне шіру Таырыбы Дербес компьютерлердегі macos операциялы жйелерін жаарту.docx