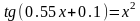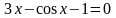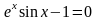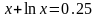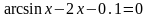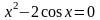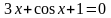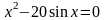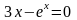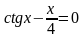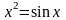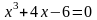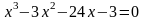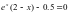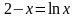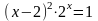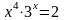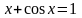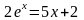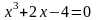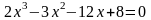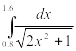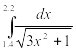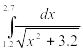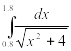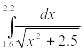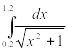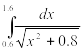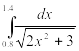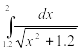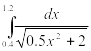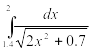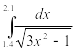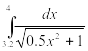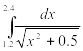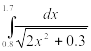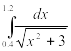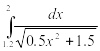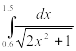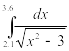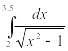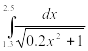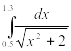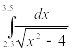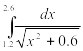МОДУЛЬ 2

ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ на базе систем

компьютерной математики

САМОСТОЯТЕЛЬНАЯ РАБОТА №1

приближенные решения нелинейных алгебраических уравнений

Цель: изучить основные методы приближенного решения нелинейных уравнений с помощью приложения Smath Studio

Вопросы для самоконтроля

1. Какие существуют способы исследования функции?

2. Какие методы используют для нахождения корней уравнения?

3. Для чего используют процедуру отделения корней?

4. В чем суть метода дихотомии?

5. В чем суть методов хорд и Ньютона? Что общего между этими методами?

6. Критерии остановки итерационного процесса.

4.1.5 Индивидуальные задания

Найти приближенные решения нелинейных алгебраических уравнений. Отделить корни заданого уравнения. Если корней несколько, то уточнить один из них указанными методами (табл)

(А) – методом половинного деления (дихотомии);

(Б) – методом хорд;

(В) – методом касательных (методом Ньютона).

Сравнить результаты, полученные разными методами. Сделать проверку.

Таблица 1– Варианты заданий

Вариант	Уравнение	Метод	Вариант	Уравнение	Метод
1		А В	14		А В
2		А В	15		А В
3		А В	16		А В
4		А В	17		Б В
5		А В	18		А В
6		А В	19		А Б
7		А В	20		Б В
8		Б В	21		А Б
9		А В	22		Б В
10		Б В	23		Б В
11		А Б	24		А Б
12		А Б	25		Б В
13		Б В

Пример выполнения задания

Найти приближенные решения нелинейных алгебраических уравнений. Отделить корни заданого уравнения. Если корней несколько, то уточнить один из них указанными методами.

(А) – методом половинного деления (дихотомии);

(Б) – методом хорд;

(В) – методом касательных (методом Ньютона).

Сравнить результаты, полученные разными методами. Сделать проверку.

Методические рекомендации

Решения уравнений приближенными методами будем находить, используя основные элементы программирования, а именно циклические оперторы. Наличие и количество корней уравнения определяем графически, изолируя корни, уточням их приближенными методами.

1. Задаем функцию.

2. Рассмотим метод половинного деления.

2.1. Рассчитываем длину отрезка, на котором уточняется корень, как разницу между концами отрезка.

2.2. Используя цикл while, уточняется корень. Находим середину отрезка и, с помощью операторов условного перехода, из двух половин выберем ту половину, на концах которой функция имеет разные знаки.

---

2.3. Цикл повторяется до тех пор, пока длина исследуемого отрезка не станет больше заданного числа ε.

Листинг программы в SMathStudio:

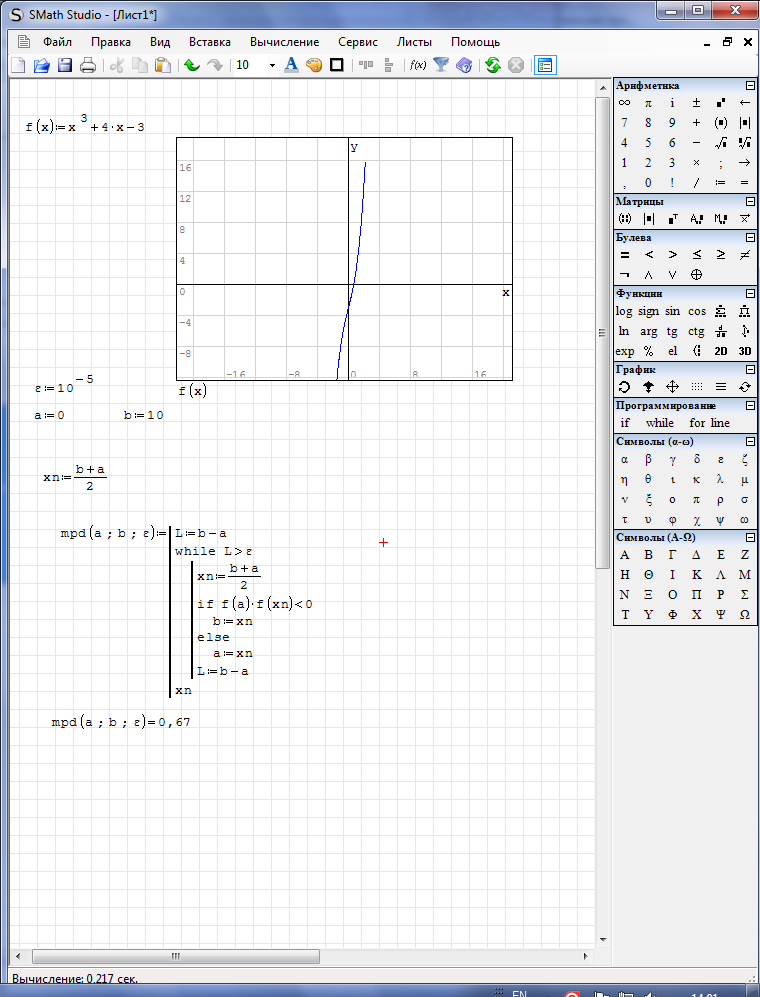
3. Рассмотрим метод хорд.

3.1. Задаем вычисление второй производной функции.

3.2. Используя условный оператор, проверяем знак выражения f(a)f(a). В зависимости от знака, метод хорд имеет два решения.

3.3. Используя цикл while, уточняем корень.

3.4. Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: |f(xn)| ≤ .

Листинг программы в SMathStudio:

где n –количество итераций. Заданная точность достигнута на 233 итерации.

4. Рассмотрим метод Ньютона.

4.1. Задаем вычисления первой и второй производных функции.

4.2. Используя условный оператор, проверяем знак выражения f(a)f(a).

4.3. Используя цикл while, уточняем корень. По формуле вычисляем точку пересечения касательной с осью абцисс.

Листинг программы в SMathStudio:

Заданная точность достигнута на восьмой итерации.

Результаты, полученные с использованием разных методов, совпадают. Для данного нелинейного уравнения выбор того или иного приближенного метода решения зависит от скорости сходимости итерационного процесса.

САМОСТОЯТЕЛЬНАЯ РАБОТА № 2

Численное интергрирование

Цель: изучить методы численного интегрирования, используя приложение Smath Studio.

Вопросы для самоконтроля

1. Геометрический смысл определенного интеграла.

2. В чем отличие приближенного нахождение определенного интеграла методами прямоугольников (квадратурными формулами) от метода трапеций?

3. Какие приближенные методы дают более точное решение и почему?

Индивидуальные задания

Найти приближенное значение интеграла заданной функции у=f(x) (таблица 2) на отрезке [a, b] различными методами.

(А) – левых прямоугольников;

(Б) - правых прямоугольников;

(В) – трапеций.

Найти значение интеграла встроенными функциями Smath. Сравнить результаты.

Таблица 2‑ Варианты заданий

Вариант	Инеграл	Метод	Вариант	Интеграл	Метод
1		А, В	14		А, В
2		А,Б	15		Б, В
3		А, В	16		Б, В
4		Б,В	17		А,Б
5		Б, В	18		А, В
6		А,В	19		А, Б
7		А, В	20		Б, В
8		А, Б	21		А,В
9		Б, В	22		А, В
10		Б, В	23		А, Б
11		А,В	24		Б, В
12		А, В	25		Б, В
13		А, Б

Пример выполнения задания

Найти приближенное значение интеграла заданной функции у=f(x) (на отрезке [a, b] различными методами.

(А) – левых прямоугольников;

---

(Б) - правых прямоугольников ;

(В) – трапеций.

Найти значение интеграла встроенными функциями Smath. Сравнить результаты.

Методические рекомендации

1. Задаем функцию.

2. Задаем значения границ отрезка интегрирования и число точек разбиения отрезка.

3. Рассчитываем длину отрезка разбиения h.

4. По формулам находим приближенные решения.

5. Проверить полученный результат можно с помощью встроенных функций.

Замечания. 1) Вычисление интеграла в пакете Smath осуществляется по формуле Симпсона (метод парабол). Метод Симпсона дает абсолютно точное значение интеграла. Это связано с тем, что первообразная функция является полиномом четвертого порядка, для которых метод Симпсона дает точное значение.

2) точность полученного решения зависит от количества шагов разбиения отрезка.

Листинг программы в Smath.

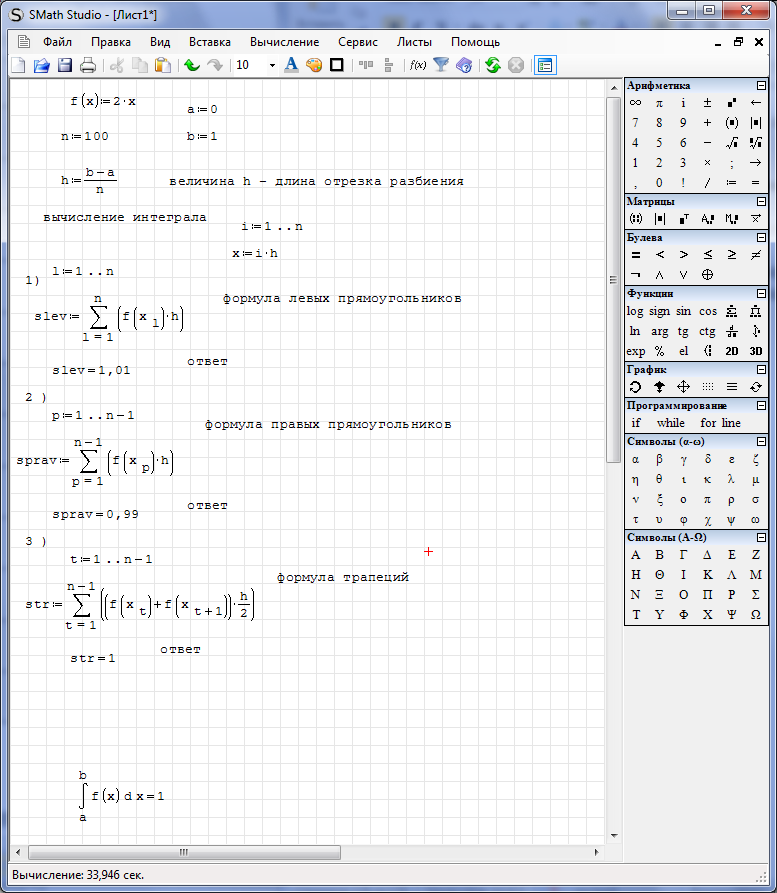
Как видно из полученного решения, для данной подинтегральной функции формула левых прямоугольников дает приближенное значение с избытком, а формула правых прямоугольников – с недостатком. Хорошую точность дает метод трапеций.

---

Смотрите также файлы

• pravo.docx

• Курочкина Л.А. Принципы и нормы Совета Европы в уголовном судопроизводстве Российской Федерации.doc

• Тройничный нерв.docx

• Лекция № 9 Организация работы редакции журнала.doc

• LABOR5.doc