Файл: Исследование плоского рычажного механизма.docx

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯРОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждениевысшего образованияСАНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТКафедра машиностроениеРасчетно-графическая работа 1.По дисциплине Теория машин и механизмов. ^{(наименование учебной дисциплины согласно учебному плану)}Тема работы: Исследование плоского рычажного механизма Выполнил: студент гр. ИТО-21 Трубчанинов Е.В ^{(шифр группы) (подпись) (Ф.И.О.)}Оценка:Дата: Проверил руководитель работы: ассистент Плащинский В.А. ^{(должность) (подпись) (Ф.И.О.)}Санкт-Петербург2023ВВЕДЕНИЕКулисный механизм – рычажный механизм, преобразующий вращательное или качатаельное движение в возвратно – поступательное и наоборот. Данное устройство классифицируется на три типа: вращающийся тип, качающийся тип или движущийся прямолинейно. Основным преимуществом данного механизма является обеспечение довольно высокой скорости ползуна, которую он развивает при выполнении обратного хода. Данное преимущество привело к тому, что такое устройство стало очень широко использоваться в том оборудовании, которое имеет холостой обратный ход.Движение механизмов зависит от их строения и сил, действующих на них. Поэтому удобно при анализе механизмов разбить работу на две части:-структурный и кинематический анализ;-кинетостатический анализ механизмов.Структурный и кинематический анализы механизмов сводятся к изучению теории строения механизмов, исследования движения тел, их образующих, с геометрической точки зрения, независимо от сил, вызывающих движение.

Исходные данные

В данном расчетно-графическом задании проводится кинематическое исследование механизма перемещения долбяка. Исследуемый механизм изображен на рис.1. Исходные данные представлены в таблице 1.

---

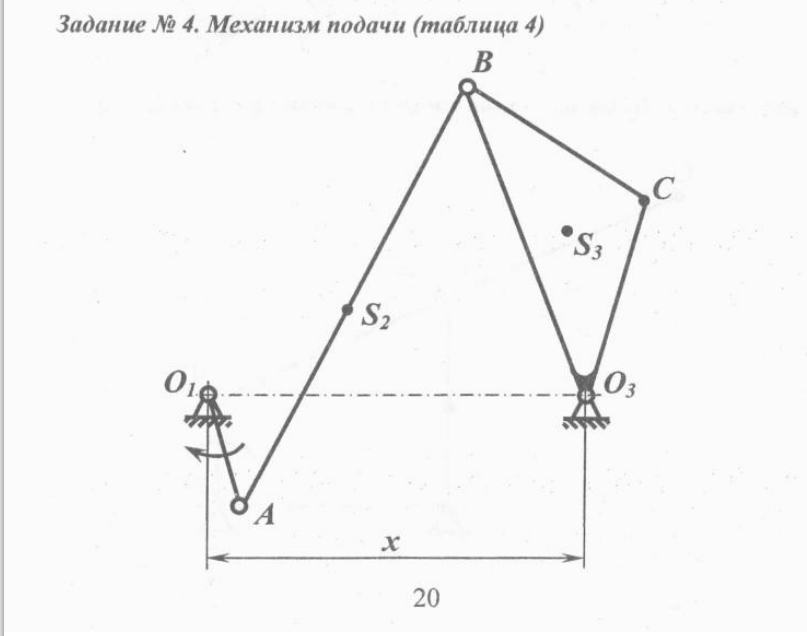
Рисунок 1 – Механизм подачи.Таблица 1 – Исходные данные

Параметр	Размерность	Вариант 2
O1A	м	0,08
B	м	0,16
BC	м	0,095
X(О1О3)	м	0,384
AB	м	0,32
О3С	м	0,095
n	мин-1	175

1. План положений механизма

Построим план положений механизма для одного цикла его движения. 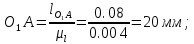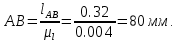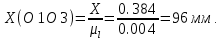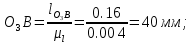Под циклом для заданного механизма принимается полный оборот кривошипа.Для построения принимаем масштабный коэффициент длины µ_l=0.004м/мм.Далее переводим все геометрические линейные размеры в масштабный коэффициент длин и получаем величины отрезков, изображающие заданные геометрические параметры в составе соответствующей кинематической схемы:Используя полученные величины отрезков геометрических параметров механизма, методом засечек, строим его кинематическую схему.Для этого на плоскости произвольно выбираем точку 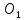(центр вращения кривошипа) 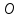и через нее проводим окружность радиусом 20 мм. Далее от 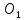откладываем горизонтальную линию размером 96 мм и получаем точку 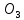. Из точки 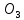также проводим окружность радиусом 40 мм – это и будет траектория движения точки В.Сначала определяем крайние положения. Крайнее левое положение будет при O1A+ AB. А крайнее правое положение при AB-O1A. Потом определяем рабочий ход механизма. У меня это с правого крайнего положения по левое крайнее положение. Откладываем от начала рабочего хода 12 равных секторов, чтобы построить все положения вместе с холостым и рабочим ходом. И получаем план положений:

---

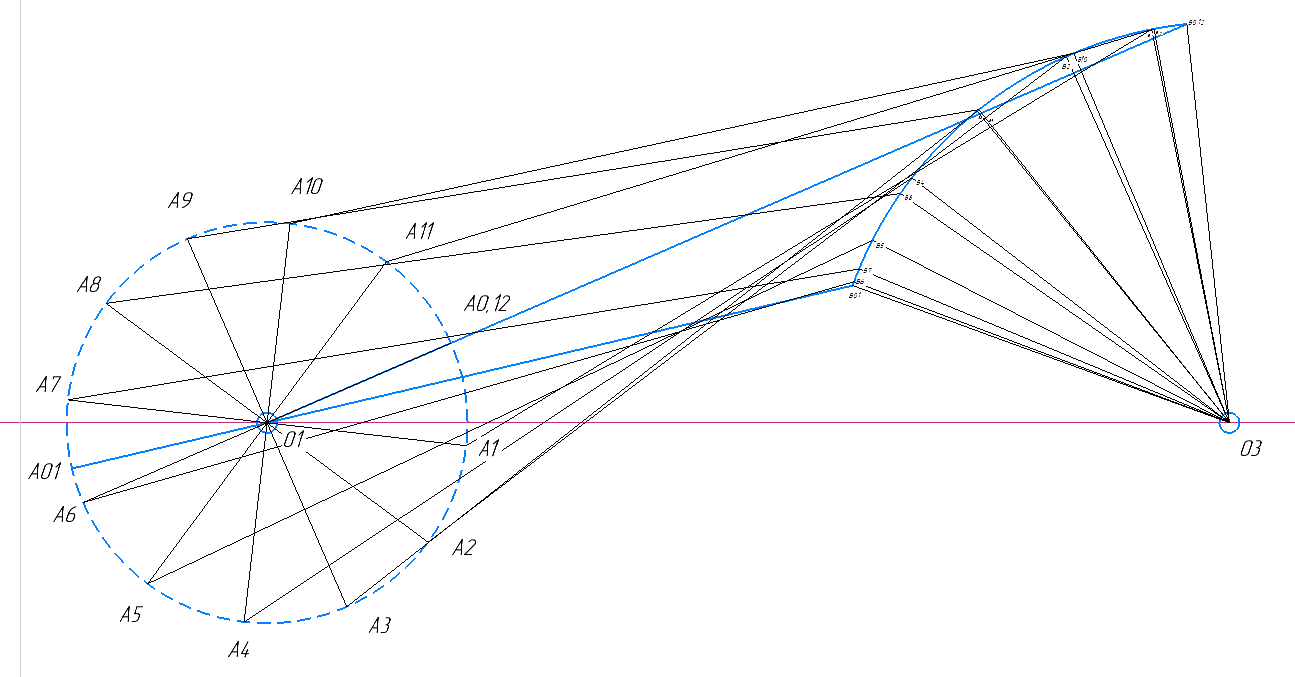
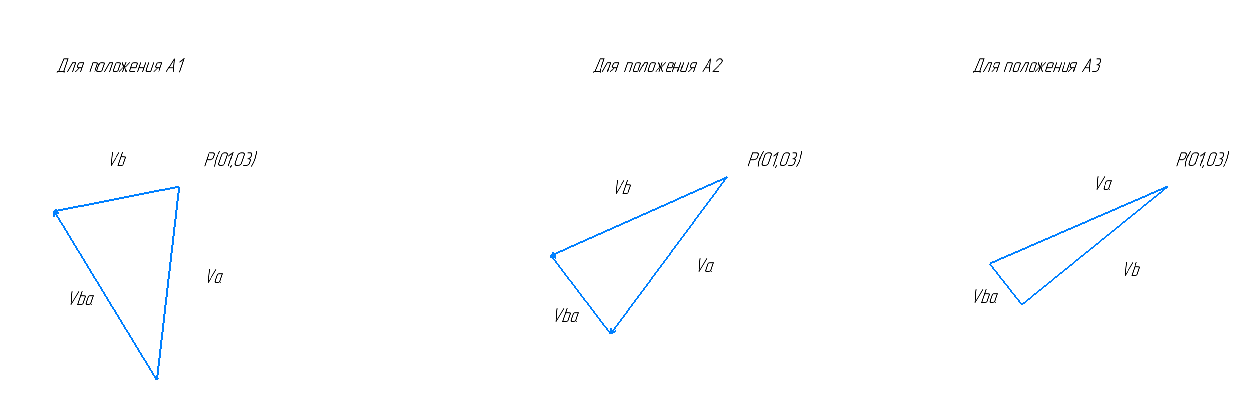
3. План скоростей

Для определения скоростей механизма воспользуемся методом построения плана скоростей. Метод заключается в построении векторов скоростей точек данного механизма в полярной системе координат с центром в точке p(полюс).Рассмотрим последовательность построения плана скоростей на примере Положения 1.Так как угловая скорость ведущего звена постоянна ( 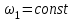), то по заданной частоте вращения кривошипа определяем её величину:Зная величину 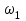определяем модуль скорости точки A и С: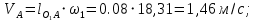Масштабный коэффициент плана скоростей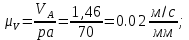Запишем векторные уравнения распределения скоростей, последовательно решая которые построим план скоростей.Скорость точки B определяем с системы уравнений: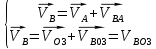Решим систему графически. Для этого из полюса проводим вектор перпендикулярно к звену АО₁, из начала этого вектора проводим прямую, перпендикулярную АВ, а из начала полиса проводим прямую, перпендикулярную ВО₃. 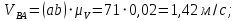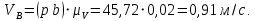Эти две прямые пересекаются, мы получаем искомые вектора.Определяем скорости для положения 1:.Аналогично находим скорости и для других положений. Полученные данные приведены в таблице 1.Таблица 1 – Величины скоростей

№ положения	1	2	3	4	5	6
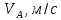	1,46	1,46	1,46	1,46	1,46	1,46
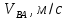	1,42	0,7	0,375	1,266	1,74	1,63
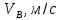	0,91	1,38	1,354	1,13	0,83	0,3

---

4. План ускорений

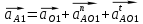
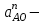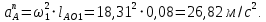
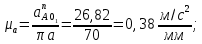
Ускорение точки A определяем с уравнения:где а_O – ускорении точки O=0, так как она неподвижна;нормальное ускорение точки A. Его величина:Масштабный коэффициент плана ускорений равен:где p_aa – произвольно выбранный отрезок, изображающий на плане ускорений модуль вектора нормального ускорения 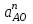кривошипа.На произвольном месте ставим точку π_a – полюс. Так как точка О₁ являются неподвижной, то на плане ускорений она будут совпадать с полюсом плана. Далее из точки p_a проводим линию параллельную кривошипу АO1 в сторону центра его вращения (от точки А к точке О1 на плане положения) и откладываем на ней расстояние p_aа, ставим точку а.У звеньев, совершающих вращательные движения, кроме нормальных ускорений 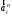(центростремительных), присутствуют и тангенциальные 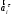(касательные). 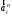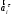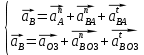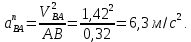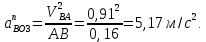При этом вектор всегда направлен вдоль оси звена к центру его вращения, а вектор направлен перпендикулярно оси звена (по касательной к окружности вращения).Ускорение точки В определяем с системы уравнений:Величина ускорения равнаОпределяем длины векторов ускорений

---

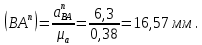
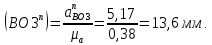
Графически решаем данную систему и определяем ускорения. Для этого из точки aпроводим параллельную прямую отрезку ba, заданной величины, это будет вектор нормального ускорения ba. Из полюса проводим также параллельную прямую нужного направления, заданной величины, и получаем искомый вектор нормального ускорения bo3. Дальше из концов этих двух векторов проводим перпендикулярные линии, которые пересекутся в точке b. Потом из полюса до точки b мы соединяем вектор, и также делаем из точки a до точки b. Тем самым находим искомые ускорения a_BAи a_B. 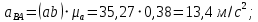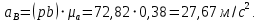Ускорения равны:Записываем данные в таблицу 2.Таблица 2 – Величины ускорений

№ положения	1	4
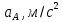	26,82	26,82
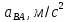	13,4	9,24
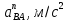	6,3	5
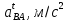	11,83	7,77
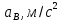	27,67	17,48
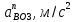	5,17	7,98
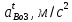	27,18	15,55

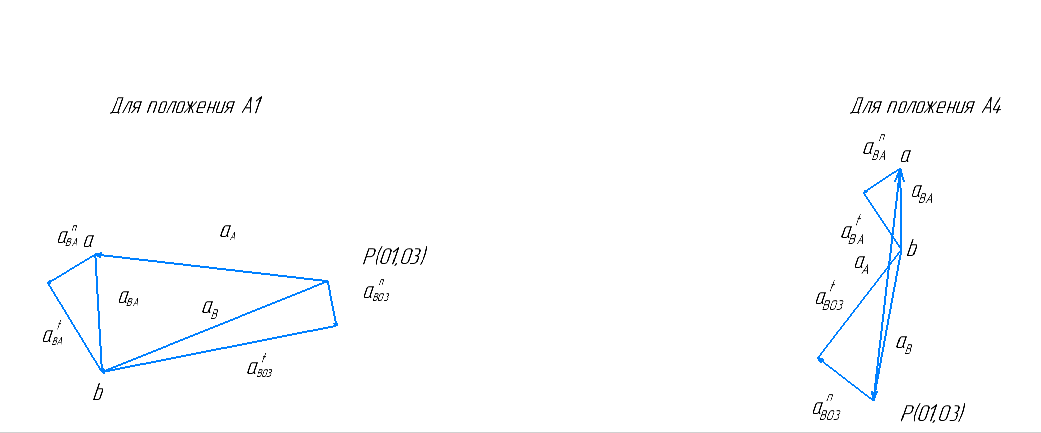
Вывод: В данной работе мы научились строить план положений механизма, план скоростей и их ускорений, а также высчитывать все эти значения.

---