МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждениевысшего образования«МИРЭА – Российский технологический университет» РТУ МИРЭАОТЧЕТПО ПРАКТИЧЕСКОЙ РАБОТЕ №1Оценка сложности и определение эффективности алгоритмапо дисциплине«Структуры и алгоритмы обработки данных»

Выполнил студент группы	11

Практическая работа выполнена	«__» февраля 2023 г.	Гошков А.А..
		(подпись студента)
«Зачтено»	«__» _________2023 г.	Ермаков С.Р.
		(подпись руководителя)

Москва 2023

СОДЕРЖАНИЕ

1. ЦЕЛЬ РАБОТЫ

Цель: Приобретение практических навыков по определению:

• 
  сложности алгоритмов на теоретическом и практическом уровнях;
  
• 
  эффективного алгоритма решения задачи из нескольких.
  

2. ХОД РАБОТЫ

   1. Задание 1

      1. Постановка задачи

Определить эффективный алгоритм из двух предложенных, используя оценку теоретической сложности каждого из алгоритмов и емкостную сложность, решения следующей задачи: дан массив из n элементов целого типа, удалить из массива все значения равные заданному.

---

2. Алгоритм 1

   1. Модель решения поставленной задачи

      1. Описание работы алгоритма

Рассмотрим первый алгоритм. Имеем функцию defFirstMethod(x, n, key), где x – массив, n – его длина, key – значение (далее ключ), которое необходимо удалить. После идет цикл, внутри которого происходит изменение массива согласно следующей логике: если значение ячейки массива с индексом i равняется ключу, то все идущие после значения сдвигаются на единицу влево, размер массива так же уменьшается на единицу. В противном же случае значения ячеек не сдвигаются, размер массива не изменяется. Происходит переход к следующей ячейке. 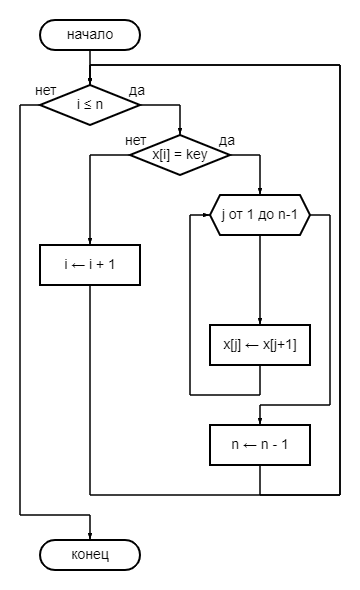Принцип работы алгоритма проиллюстрирован на рисунке 1.Рисунок 1 – Блок-схема алгоритма 1

2. Инвариант цикла

Возьмем в качестве инварианта следующее утверждение: значение переменной i всегда меньше n + 2 (i < n + 2). Докажем корректность инварианта: как наглядно проиллюстрировано на рисунке 1, внешний цикл проходит по значениям от 1 до n включительно. На значении n + 1 условие входа в цикл перестает выполняться и алгоритм подходит к своему логическому концу. Внутри цикла разница между значениями i и n при каждом проходе уменьшается на единицу (так как либо увеличивается значение i, либо уменьшается значение n), в следствие чего не может быть ситуации, когда разница значений изменится скачкообразным образом, например, с i <= n (i = 4, n = 8) на i > n (i = 777, n = 8).

3. Теоретическая вычислительная сложность алгоритма

Рассчитаем сложность алгоритма, используя теоретический подход (см. таблица 1)Таблица 1 – Определение функции роста

Номер оператора	Оператор	Время выполнения 1-го оператора	Кол-во выполнений в строке
1	int i = 0;	C1	1
2	while (i < n) {	C2	n + 1
3	if (x[i] == key) {	C3	n
4	for (int j = i; j < n - 1; j++)	C4	n2
5	x[j] = x[j + 1];	C1	n2
6	n--;	C5	n
7	} else i++	C5	n
	}

---

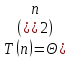
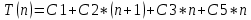
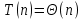
Определим функцию порядка роста для худшего случая:Таким образом Определим функцию порядка роста для лучшего случая:Таким образом В среднем случае функция роста 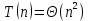, так как вложенный цикл выполнится хотя бы 1 раз (по определению среднего случая).

2. Реализация алгоритма 1 и дополнительной логики на языке С++

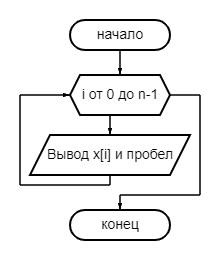
Необходимо реализовать алгоритм defFirstMethod, поместить в него операторы для подсчета числа выполненных сравнений и элементов при удалении, вывод массива на экран, заполнение его случайными числами. Блок схемы функций можно наблюдать на рисунках 2 – 5. 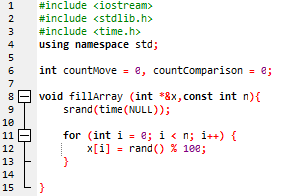Код можно видеть на рисунках 6 – 9.Рисунок 2 – Блок-схема функции fillArrayРисунок 3 – Блок-схема функция showArrayРисунок 4 – Блок-схема функция delFirstMetodРисунок 4 – Блок-схема функции mainРисунок 6 – Функция fillArrayРисунок 7 – Функция showArrayРисунок 8 – Функция delFirstMetodРисунок 9 – Функция main

3. Тестирование программы на 10 и 100 значениях

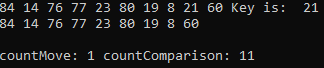
Проведем тесты программы на 10 и 100 значениях (рис. 10 – 15).Рисунок 10 – Тест при 10 значениях

---

Рисунок 11 – Тест при 100 значенияхРисунок 12 – Тест худшего случая при 10 значенияхРисунок 13 – Тест худшего случая при 100 значенияхРисунок 14 – Тест лучшего случая при 10 значенияхРисунок 15 – Тест лучшего случая при 100 значенияхЗаметим, что в лучшем случае при увеличении размера вводных данных в 10 раз (с 10 до 100) суммарное количество операций меняется с 10 до 100, то есть время выполнения зависит от вводимых данных линейно, что совпадает с теоретической оценкой. В худшем случае суммарное количество операций меняется с 65 до 5150, то есть время выполнения зависит от вводимых данных квадратично, что совпадает с теоретической оценкой.

3. Алгоритм 2

   1. Модель решения поставленной задачи

      1. Описание работы алгоритма

Рассмотрим первый алгоритм. Имеем функцию delOtherMetod(x, n, key), где x – массив, n – его длина, key – значение (далее ключ), которое необходимо удалить. После идет цикл от переменной i, внутри которого происходит изменение массива согласно следующей логике: ячейке массива под индексом j (изначально j – индекс первого элемента) присваивается значение ячейки массива под индексом i. Если присвоенное значение не нужно удалять, то значение переменной j увеличивается на 1. Вне цикла (после его выполнения) переменной n присваивается значение переменной j. 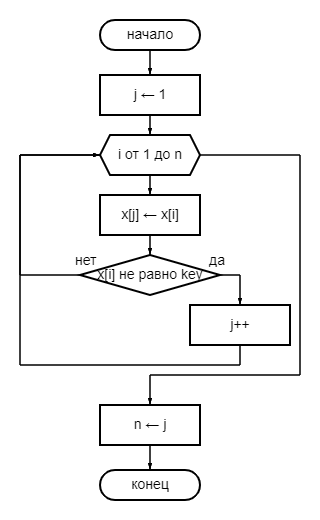Принцип работы алгоритма проиллюстрирован на рисунке 16.Рисунок 16 – Блок-схема алгоритма delOtherMetod

2. Инвариант цикла

Возьмем в качестве инварианта следующее утверждение: значение переменной i всегда меньше n + 2 (i < n + 2). Докажем корректность инварианта: как наглядно проиллюстрировано на рисунке 1, цикл проходит по значениям от 1 до n включительно. На значении n + 1 условие входа в цикл перестает выполняться и алгоритм подходит к своему логическому концу. Внутри цикла разница между значениями i и n при каждом проходе уменьшается на единицу (так как либо увеличивается значение i, либо уменьшается значение n), в следствие чего не может быть ситуации, когда разница значений изменится скачкообразным образом, например, с i <= n (i = 4, n = 8) на i > n (i = 777, n = 8).

---

3. Теоретическая вычислительная сложность алгоритма

Рассчитаем сложность алгоритма, используя теоретический подход (см. таблица 2).Таблица 2 – Определение функции роста

Номер оператора	Оператор	Время выполнения 1-го оператора	Кол-во выполнений в строке
1	int j = 0;	C1	1
2	for (int i = 0; i < n; i++){	C2	n + 1
3	x[j] = x[i];	C1	n
4	if (x[i] != key)	C3	n
5	j++;	C4	n
6	}
7	n = j;	C1	1
	}

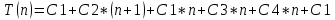
Определим функцию порядка роста для худшего случая:Таким образом Определим функцию порядка роста для лучшего случая:Таким образом В среднем случае функция роста , так как и худший, и лучший случаи имеют функцию роста .

2. Реализация алгоритма 1 и дополнительной логики на языке С++

Необходимо реализовать алгоритм delOtherMetod, поместить в него операторы для подсчета числа выполненных сравнений и элементов при удалении, вывод массива на экран, заполнение его случайными числами. Блок схемы функций можно наблюдать на рисунках 17 – 20. Код можно видеть на рисунках 21 – .Рисунок 17 – Блок-схема функции fillArray

---

Смотрите также файлы

• Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Конституционное право Практическое задание 3.docx

• Необходим для подключения компьютера к локальной или глобальной сети.pdf

• Таиланд Географическое положение.pdf

• Виды креселколясок для людей с дцп.pptx

• Учебное пособие по гистологии тема пищеварительная система. Передний отдел. Ротовая полость. Развитие и строение зубов. .pdf