ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx - Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx - G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
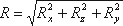
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что
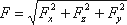
2.5. Закон Архимеда и его приложение
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
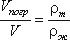
где: V - объем плавающего тела;
ρm - плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
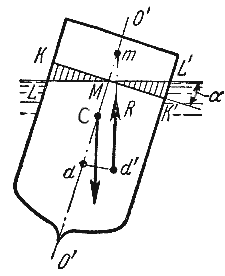
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
2.6. Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
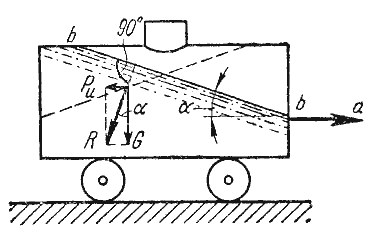
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая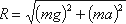
этих сил направлена к вертикали под углом α, тангенс которого равен
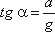
Так как свободная поверхность, как поверхность равного давления
, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu = mω2r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.
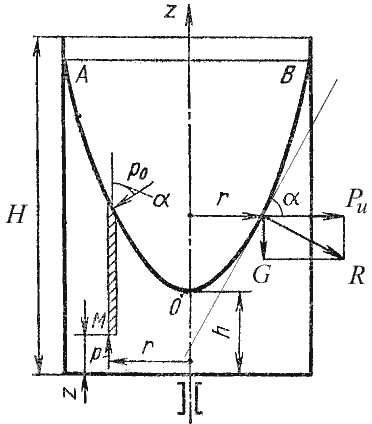
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
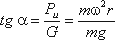
С другой стороны:
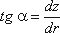
где z - координата рассматриваемой точки. Таким образом, получаем:
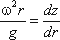
откуда
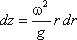
или после интегрирования
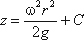
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
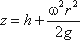
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
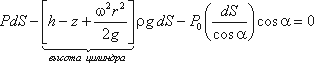
После сокращений получим
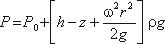
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
ТЕСТ ПО ЛЕКЦИИ №2
2.1. Как называются разделы, на которые делится гидравлика?
а) гидростатика и гидромеханика;
б) гидромеханика и гидродинамика;
в) гидростатика и гидродинамика;
г) гидрология и гидромеханика.
2.2. Раздел гидравлики, в котором рассматриваются законы равновесия жидкости называется
а) гидростатика;
б) гидродинамика;
в) гидромеханика;
г) гидравлическая теория равновесия.
2.3. Гидростатическое давление - это давление присутствующее
а) в движущейся жидкости;
б) в покоящейся жидкости;
в) в жидкости, находящейся под избыточным давлением;
г) в жидкости, помещенной в резервуар.
2.4. Какие частицы жидкости испытывают наибольшее напряжение сжатия от действия гидростатического давления?
а) находящиеся на дне резервуара;
б) находящиеся на свободной поверхности;
в) находящиеся у боковых стенок резервуара;
г) находящиеся в центре тяжести рассматриваемого объема жидкости.
2.5. Среднее гидростатическое давление, действующее на дно резервуара равно
а) произведению глубины резервуара на площадь его дна и плотность;
б) произведению веса жидкости на глубину резервуара;
в) отношению объема жидкости к ее плоскости;
г) отношению веса жидкости к площади дна резервуара.
2.6. Первое свойство гидростатического давления гласит
а) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует от рассматриваемого объема;
б) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема;
в) в каждой точке жидкости гидростатическое давление действует параллельно площадке касательной к выделенному объему и направлено произвольно;
г) гидростатическое давление неизменно во всех направлениях и всегда перпендикулярно в точке его приложения к выделенному объему.
2.7. Второе свойство гидростатического давления гласит
а) гидростатическое давление постоянно и всегда перпендикулярно к стенкам резервуара;
б) гидростатическое давление изменяется при изменении местоположения точки;
в) гидростатическое давление неизменно в горизонтальной плоскости;
г) гидростатическое давление неизменно во всех направлениях.
2.8. Третье свойство гидростатического давления гласит
а) гидростатическое давление в любой точке не зависит от ее координат в пространстве;
б) гидростатическое давление в точке зависит от ее координат в пространстве;
в) гидростатическое давление зависит от плотности жидкости;
г) гидростатическое давление всегда превышает давление, действующее на свободную поверхность жидкости.
2.9. Уравнение, позволяющее найти гидростатическое давление в любой точке рассматриваемого объема называется
а) основным уравнением гидростатики;
б) основным уравнением гидродинамики;
в) основным уравнением гидромеханики;
г) основным уравнением гидродинамической теории.
2.10. Основное уравнение гидростатики позволяет
а) определять давление, действующее на свободную поверхность;
б) определять давление на дне резервуара;
в) определять давление в любой точке рассматриваемого объема;
г) определять давление, действующее на погруженное в жидкость тело.
2.11. Среднее гидростатическое давление, действующее на дно резервуара определяется по формуле
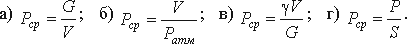
2.12. Основное уравнение гидростатического давления записывается в виде
2.13. Основное уравнение гидростатики определяется
а) произведением давления газа над свободной поверхностью к площади свободной поверхности;
б) разностью давления на внешней поверхности и на дне сосуда;
в) суммой давления на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев;
г) отношением рассматриваемого объема жидкости к плотности и глубине погружения точки.
2.14. Чему равно гидростатическое давление при глубине погружения точки, равной нулю
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx - Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx - G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что
2.5. Закон Архимеда и его приложение
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
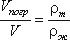
где: V - объем плавающего тела;
ρm - плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
2.6. Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая
этих сил направлена к вертикали под углом α, тангенс которого равен Так как свободная поверхность, как поверхность равного давления
, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила Pu = mω2r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
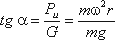
С другой стороны:
где z - координата рассматриваемой точки. Таким образом, получаем:
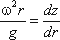
откуда
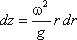
или после интегрирования
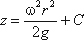
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
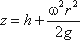
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
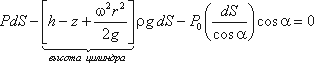
После сокращений получим
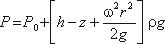
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
ТЕСТ ПО ЛЕКЦИИ №2
2.1. Как называются разделы, на которые делится гидравлика?
а) гидростатика и гидромеханика;
б) гидромеханика и гидродинамика;
в) гидростатика и гидродинамика;
г) гидрология и гидромеханика.
2.2. Раздел гидравлики, в котором рассматриваются законы равновесия жидкости называется
а) гидростатика;
б) гидродинамика;
в) гидромеханика;
г) гидравлическая теория равновесия.
2.3. Гидростатическое давление - это давление присутствующее
а) в движущейся жидкости;
б) в покоящейся жидкости;
в) в жидкости, находящейся под избыточным давлением;
г) в жидкости, помещенной в резервуар.
2.4. Какие частицы жидкости испытывают наибольшее напряжение сжатия от действия гидростатического давления?
а) находящиеся на дне резервуара;
б) находящиеся на свободной поверхности;
в) находящиеся у боковых стенок резервуара;
г) находящиеся в центре тяжести рассматриваемого объема жидкости.
2.5. Среднее гидростатическое давление, действующее на дно резервуара равно
а) произведению глубины резервуара на площадь его дна и плотность;
б) произведению веса жидкости на глубину резервуара;
в) отношению объема жидкости к ее плоскости;
г) отношению веса жидкости к площади дна резервуара.
2.6. Первое свойство гидростатического давления гласит
а) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует от рассматриваемого объема;
б) в любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема;
в) в каждой точке жидкости гидростатическое давление действует параллельно площадке касательной к выделенному объему и направлено произвольно;
г) гидростатическое давление неизменно во всех направлениях и всегда перпендикулярно в точке его приложения к выделенному объему.
2.7. Второе свойство гидростатического давления гласит
а) гидростатическое давление постоянно и всегда перпендикулярно к стенкам резервуара;
б) гидростатическое давление изменяется при изменении местоположения точки;
в) гидростатическое давление неизменно в горизонтальной плоскости;
г) гидростатическое давление неизменно во всех направлениях.
2.8. Третье свойство гидростатического давления гласит
а) гидростатическое давление в любой точке не зависит от ее координат в пространстве;
б) гидростатическое давление в точке зависит от ее координат в пространстве;
в) гидростатическое давление зависит от плотности жидкости;
г) гидростатическое давление всегда превышает давление, действующее на свободную поверхность жидкости.
2.9. Уравнение, позволяющее найти гидростатическое давление в любой точке рассматриваемого объема называется
а) основным уравнением гидростатики;
б) основным уравнением гидродинамики;
в) основным уравнением гидромеханики;
г) основным уравнением гидродинамической теории.
2.10. Основное уравнение гидростатики позволяет
а) определять давление, действующее на свободную поверхность;
б) определять давление на дне резервуара;
в) определять давление в любой точке рассматриваемого объема;
г) определять давление, действующее на погруженное в жидкость тело.
2.11. Среднее гидростатическое давление, действующее на дно резервуара определяется по формуле
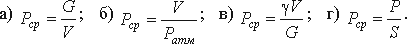
2.12. Основное уравнение гидростатического давления записывается в виде
2.13. Основное уравнение гидростатики определяется
а) произведением давления газа над свободной поверхностью к площади свободной поверхности;
б) разностью давления на внешней поверхности и на дне сосуда;
в) суммой давления на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев;
г) отношением рассматриваемого объема жидкости к плотности и глубине погружения точки.
2.14. Чему равно гидростатическое давление при глубине погружения точки, равной нулю