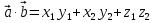Файл: Наименование организации образования Поурочный план или краткосрочный план для педагога организаций среднего образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
_______________________________________________________
(наименование организации образования)
Поурочный план или краткосрочный план для педагога организаций среднего образования
| Раздел | Прямоугольная система координат и векторы в пространстве | |||||||||||
| ФИО педагога | | |||||||||||
| Дата | | |||||||||||
| Класс « 10» | Количество присутствующих: | Количество отсутствующих: | ||||||||||
| Тема урока№53 | Скалярное произведение векторов | |||||||||||
| Цели обучения в соответствии с учебной программой | 10.4.4 –знать определение и свойства скалярного произведения векторов | |||||||||||
| Цель урока | Познакомить учащихся с понятием угла между векторами; ввести понятие скалярного произведения двух векторов, скалярного квадрата вектора; рассказать о применении скалярного произведения векторов в физике, механике; показать применение скалярного произведения векторов при решении задач; развивать логическое мышление учащихся | |||||||||||
| Ход урока | ||||||||||||
| Этап урока/время | Действия педагога | Действия учеников | Оценивание | Ресурсы | ||||||||
| Начало урока 1мин 2мин 5 мин | Настрой на урок Актуализация опорных знаний. 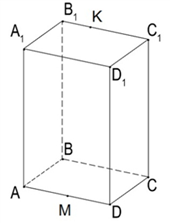 №1.  – прямоугольный параллелепипед. На данном рисунке назовите: – прямоугольный параллелепипед. На данном рисунке назовите:
Будут ли 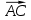 и и 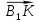 сонаправленными или противоположно направленными? сонаправленными или противоположно направленными?Мы говорили о том, что векторы применяются в различных областях наук, в том числе в физике, где встречаются векторные и скалярные величины. Кто может сказать, в чем их различие? Обратимся к следующей задаче: Парусная лодка движется под действием силы ветра. По рисунку определите, чему равна работа этой силы при перемещении лодки. 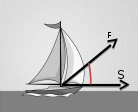 Вспомните, как найти работу через силу и перемещение. Из физики известно, что 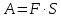 . Какими величинами, скалярными или векторными, являются работа, сила и перемещение? (Какие из этих величин характеризуются направлением?) . Какими величинами, скалярными или векторными, являются работа, сила и перемещение? (Какие из этих величин характеризуются направлением?)Итак, работа – скалярная величина, сила и перемещение – векторные величины, они имеют направление. Таким образом, над F и S мы должны поставить знак вектора. Здесь мы сталкиваемся с новым действием, которое называется скалярным произведением. Как вы думаете, какой будет цель нашего занятия? (Научиться находить скалярное произведение векторов) | Демонстрируют свои умения находить вектора по определению | Похвала Самооценка . Взаимооценивание. Оценка работы всего класса учителем. | Слайды №1-4 Слайд№5 Слайд | ||||||||
| 20мин Изучение нового материала Работа у доски разбор заданий Работа в паре | Запишем тему урока «Скалярное произведение векторов». Сначала давайте разберемся, почему произведение называется скалярным. Где мы уже встречались с таким термином? Вернемся к формуле 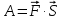 . Как уже говорили, работа – это… (скалярная величина), что это значит? (характеризуется только числом). . Как уже говорили, работа – это… (скалярная величина), что это значит? (характеризуется только числом). Исходя из этого, как вы думаете, что будет являться результатом скалярного произведения векторов? (число) Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. 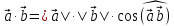 С понятием длины вектора мы уже знакомы, необходимо выяснить, что называют углом между векторами. Пусть даны два вектора 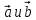 . .     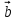 Как вы думаете, как получить угол между этими векторами? (Выслушать предложения учеников) От произвольной точки О отложим 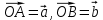 . Тогда . Тогда 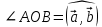 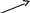       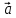 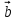 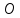 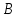 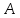 Чему равен угол между векторами, если они сонаправлены? Чему равен угол между векторами, если они противоположно направлены? Если перпендикулярны?
Вспомним, что такое косинус угла? (вспомнить и записать значения синусов и косинусов табличных углов) Геометрическая интерпретация. Скалярным произведением двух векторов 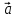 и и 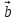 будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними: будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними: 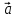 · ·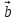 = = 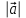 · ·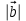 cos α cos α Дано: 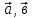 - векторы - векторы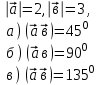 Найти: 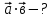 Решение: 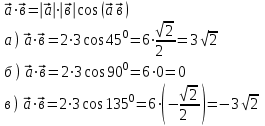 Ответ: 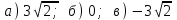 | Ребята включаются в беседу. Записывают основные формулы и свойства скалярного умножения Работа у доски с подробным пояснением. Работают в паре. | Хвала учителя. Учитель Оценивают свои работы по образцу и делают анализ работы. | Слайд 14 Слайд Слайд 15 | ||||||||
| Конец урока 2мин |
Что было сегодня необычного? Что понравилось? Домашнее задание | Записывают домашнее задание | | | ||||||||
Поурочный план или краткосрочный план для педагога организаций среднего образования
| Раздел | Прямоугольная система координат и векторы в пространстве | |||||
| ФИО педагога | | |||||
| Дата | | |||||
| Класс « 10» | Количество присутствующих: | Количество отсутствующих: | ||||
| Тема урока№54 | Скалярное произведения векторов в координатной форме. | |||||
| Цели обучения в соответствии с учебной программой | 10.4.16 – знать формулу скалярного произведения векторов в координатной форме и применять ее при решении задач | |||||
| Цель урока | Применять формулу скалярного произведения векторов в координатной форме. | |||||
| Ход урока | ||||||
| Этап урока/время | Действия педагога | Действия учеников | Оценивание | Ресурсы | ||
| Начало урока 1мин 2мин 5 мин | Настрой на урок. Проверка домашнего задания. III. Актуализация опорных знаний учащихся: Можно начертить вектор и назвать его. Каким еще способом можно задать вектор? (С помощью координат). Сколько координат имеет вектор в пространстве? №2. 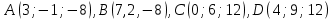
Выясните, будут ли коллинеарны векторы 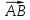 и и  ? Будут ли перпендикулярны ?Как это сделать? ? Будут ли перпендикулярны ?Как это сделать? | Разбор заданий где возникли затруднения при решении примеров. ПР Демонстрируют свои знания нахождение длины вектора Определяют равные вектора | Похвала Самооценка . Взаимооценивание. Оценка работы всего класса учителем. | Слайды №15 | ||
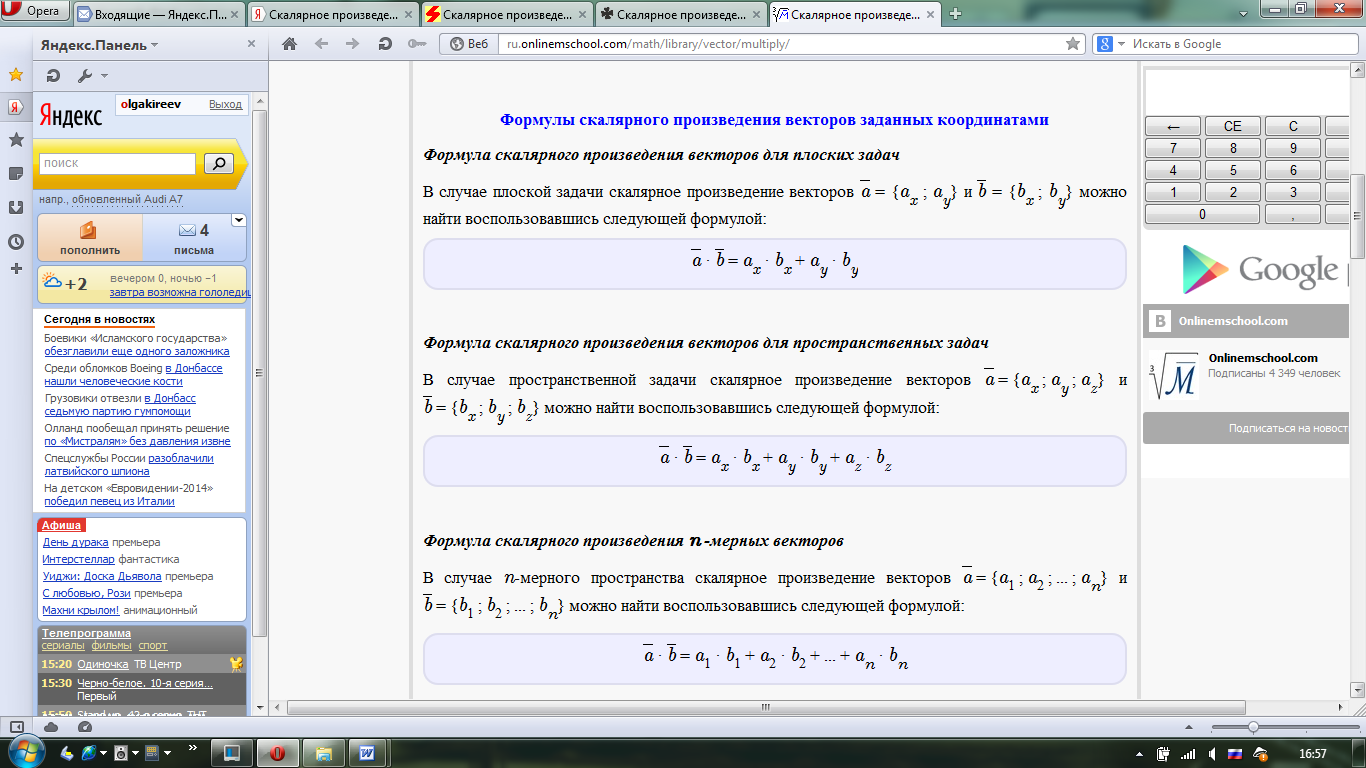
| 20мин Работа у доски разбор заданий | В координатах скалярное произведение – это сумма произведений соответствующих координат. (Доказательство данного свойства аналогично доказательству, которое приводилось в курсе планиметрии Задание№1.
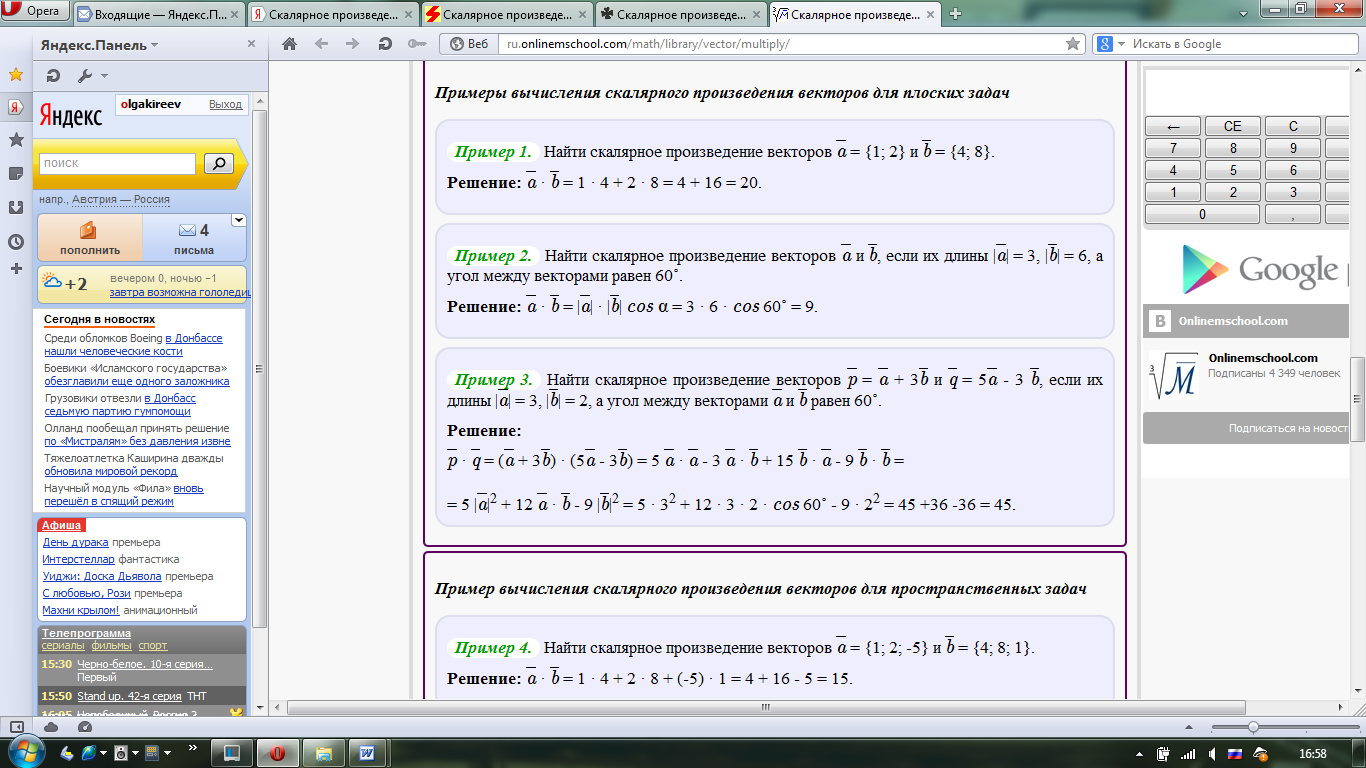
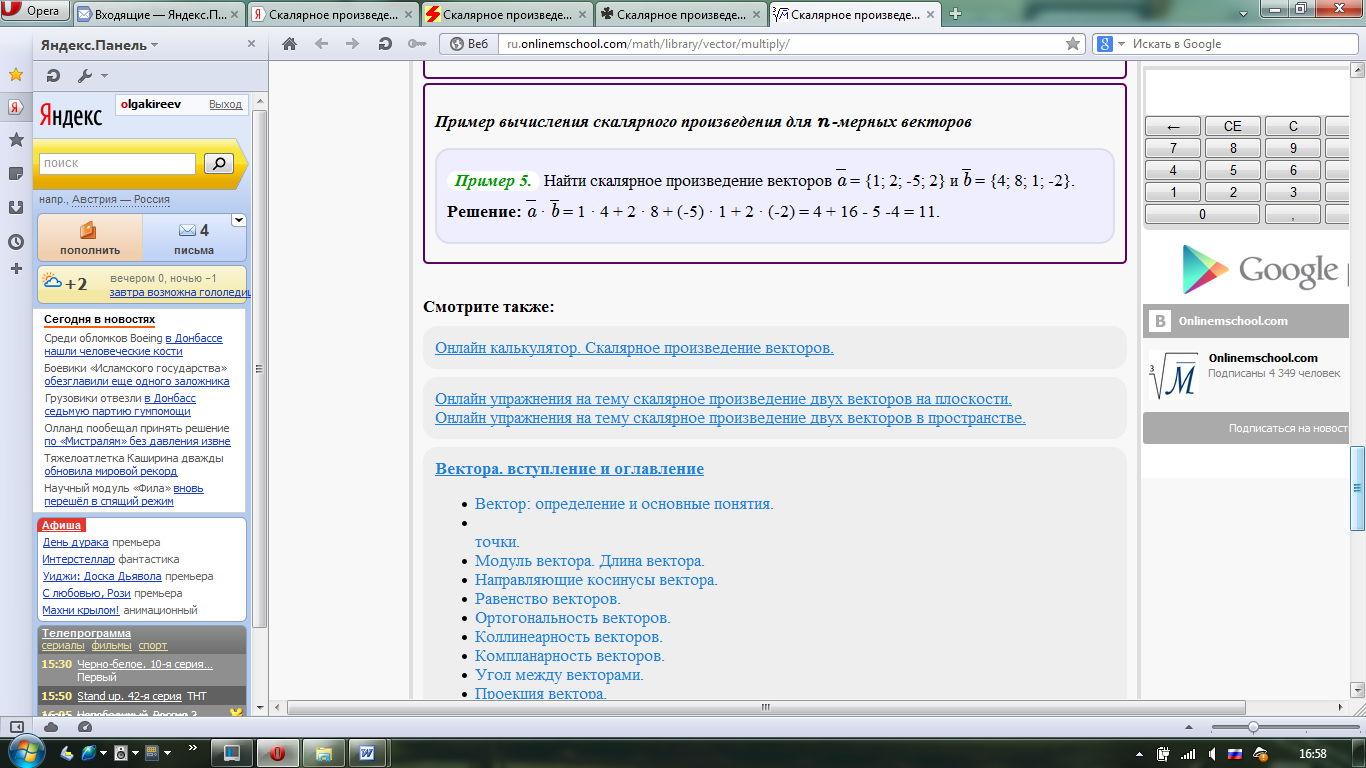
Решение: Если даны координаты векторов, то число, которое является скалярным произведением векторов, определяется следующим образом:  {xa;ya;za} b {xb;yb;zb} {xa;ya;za} b {xb;yb;zb}a⃗ ⋅b⃗ =xa⋅xb+ya⋅yb+za⋅zb=  = {1; 2} и = {1; 2} и  = {4; 8}. = {4; 8}.a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20 Ответ: 20 Решить задание
Ответ:-16
Найди значение x, если a⃗ b⃗ =8. Решение  · · = xa⋅xb+ya⋅yb+za⋅zb = xa⋅xb+ya⋅yb+za⋅zbТ.к a⃗ b⃗ =8. То 8=(-8) 1+8x+ (-4)(-2) 8=-8+8x+8 8x=8 x=1 Ответ: 1
Найди значение x, если a⃗ b⃗ =0. Ответ: 1 Найти скалярное произведение векторов 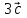 и и 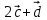 , если , если 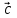 (0;-3;5) и (0;-3;5) и 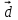 (-4;1;0) (-4;1;0) | . | Самооценивание по образцу | Слайд 16 Слайд17-19 | ||
| 10мин | ФО.      | Выполняют тест. Работают самостоятельно | Самооценивание по ключу. | Слайд20-28 | ||
| Конец урока 2мин |
Что было сегодня необычного? Что понравилось? Домашнее задание | Записывают домашнее задание | | Слайд29 | ||
Поурочный план или краткосрочный план для педагога организаций среднего образования
| Раздел | Прямоугольная система координат и векторы в пространстве | ||||||||||
| ФИО педагога | | ||||||||||
| Дата | | ||||||||||
| Класс « 10» | Количество присутствующих: | Количество отсутствующих: | |||||||||
| Тема урока№55 | Нахождение угла между векторами | ||||||||||
| Цели обучения в соответствии с учебной программой | 10.4.17 вычислять угол между двумя векторами в пространстве; | ||||||||||
| Цель урока |
| ||||||||||
| Ход урока | |||||||||||
| Этап урока/время | Действия педагога | Действия учеников | Оценивание | Ресурсы | |||||||
| Начало урока 1мин 2мин 5 мин | Настрой на урок. Проверка домашнего задания.
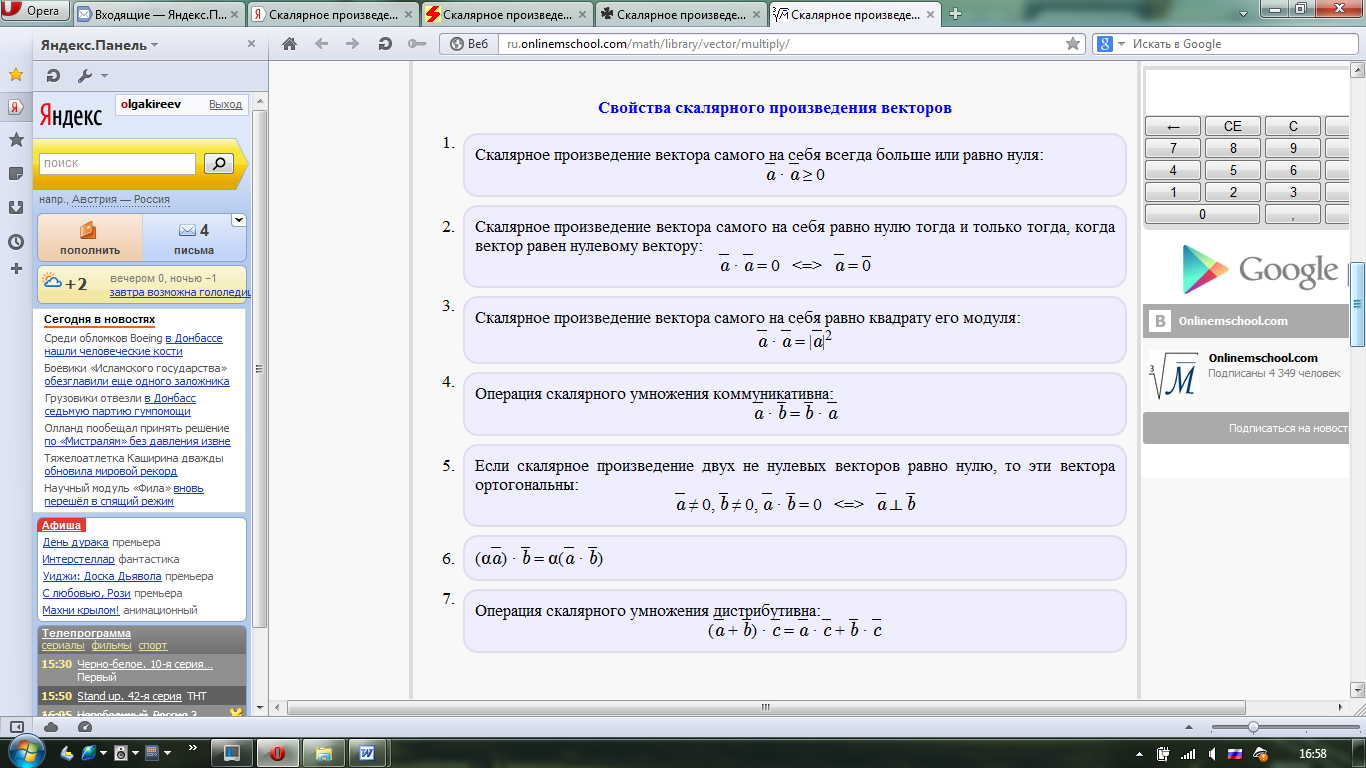
Найти скалярное произведение векторов  , если , если 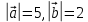 и иа) 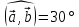 , ,б)  , ,в)  . .с) 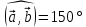 , ,Какой вывод можно сделать о скалярном произведении перпендикулярных векторов? Это первое свойство скалярного произведения. Постарайтесь сформулировать его. (Если векторы перпендикулярны, то их скалярное произведение равно нулю). Верно ли обратное? (Если скалярное произведение векторов равно нулю, то они перпендикулярны). Кроме этого, есть и другие свойства, которые имеют большое геометрическое приложение.
| Разбор заданий где возникли затруднения при решении примеров. ПР Демонстрируют свои знания нахождение длины вектора Определяют равные вектора | Похвала Самооценка . Взаимооценивание. Оценка работы всего класса учителем. | Слайды №1-4 Слайд№5 Слайд6 | |||||||
| 20мин Работа у доски разбор заданий | Косинус угла φ между векторами 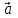 = (x1; y1; z1) и = (x1; y1; z1) и = (x2; y2; z2): = (x2; y2; z2):  | . Работают у доски с пояснением. | Самооценивание по образцу | Слайд 7 | |||||||
| 10мин | Работа в паре  ФО. Вычислите угол между прямыми векторами 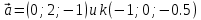 . . | Работают в парах. Работают самостоятельно | Самооценивание по ключу. Взаимооценивание. | слайд №8 Слайд 9 | |||||||
| Конец урока 2мин |
Что было сегодня необычного? Что понравилось? Домашнее задание | Записывают домашнее задание | | | |||||||
Практическое задание по теме
«Действия с векторами, заданными координатами. Скалярное произведение векторов»
Вариант 1
1. Найти скалярное произведение векторов и , если
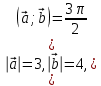
2. Найти скалярное произведение векторов , если (5;7;0) (1;1;0)
3. Найти длины векторов , если (2;-1;3) (4;0;-1)
4. Найти скалярное произведение векторов и , если (0;-3;5) и (-4;1;0)
Практическая работа №26 на тему
«Скалярное произведение векторов»
Геометрическая интерпретация. Скалярным произведением двух векторов
 и
и  будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:  ·
· =
=  ·
· cos α
cos αАлгебраическая интерпретация. Скалярным произведением двух векторов
 и
и  будет скалярная величина, равная сумме попарного произведения координат векторов
будет скалярная величина, равная сумме попарного произведения координат векторов  и
и  .
.

Косинус угла φ между векторами
 = (x1; y1; z1) и
= (x1; y1; z1) и  = (x2; y2; z2):
= (x2; y2; z2):5. Даны три вершины треугольника А(-1;0); В(3;2); С(5;-4). Найти угол АВС (угол при вершине В).
6. В пространстве задан треугольник координатами своих вершин А1(1;1;1); А2(3;0;0); А3(2;3;7). Найти угол между сторонами А1А2 и А1А3
Вариант 2
1. Найти скалярное произведение векторов
 и
и  , если
, если 
2. Найти скалярное произведение векторов
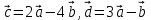 , если
, если  (2;5)
(2;5)  (3;1)
(3;1)3. Найти длины векторов
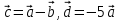 , если
, если  (1;2;-4)
(1;2;-4)  (3;-1;0)
(3;-1;0)4. Найти скалярное произведение векторов
 и
и  , если
, если  (1;2;-2) и
(1;2;-2) и  (-3;0;2)
(-3;0;2)5. Даны три вершины треугольника А(1;-2); В(2;3); С(4;-5). Найти угол АВС (угол при вершине В).
6. В пространстве задан треугольник координатами своих вершин А1(2;-1;0); А2(3;2;-1); А3(2;4;1). Найти угол между сторонами А1А2 и А1А3
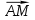 ;
;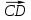 ;
;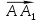 .
.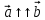
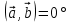
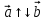
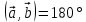
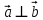
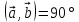
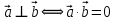
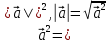
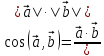 (Как из формулы выразить косинус угла?)
(Как из формулы выразить косинус угла?)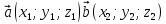 ,
,