1. 
   Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3
   

Таблица 3. Регрессионный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

Решение: Линейная регрессия. Для расчета параметров a и b линейной регрессии, построим вспомогательную таблицу:

N	x	y	x2	y2	x∙y
1	10	30	100	900	300
2	20	50	400	2500	1000
3	30	70	900	4900	2100
4	40	90	1600	8100	3600
5	50	110	2500	12100	5500
Сумма	150	350	5500	28500	12500

Система нормальных уравнений:
 
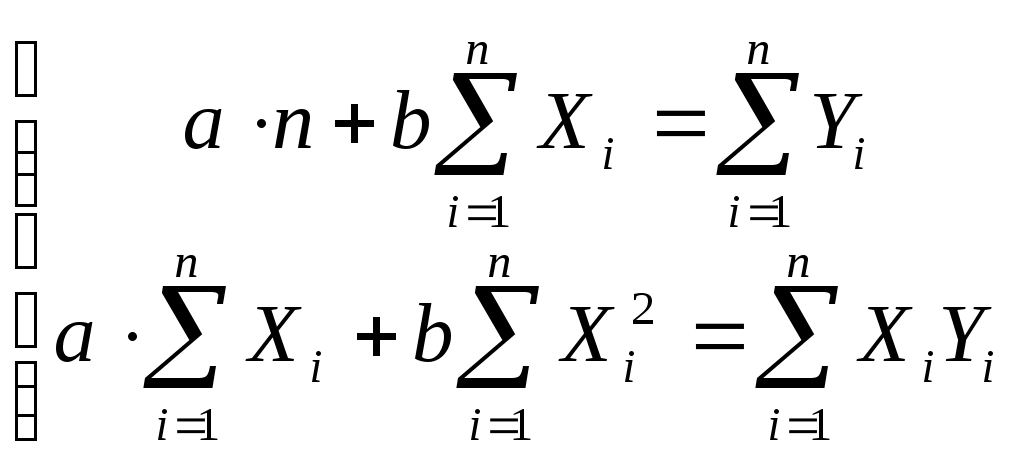
Тогда получим   , или   

---

Сложив уравнения последней системы, получим:   

Таким образом, получили:   .
Уравнение линейной регрессии:
 
Экспоненциальная регрессия. Для расчета параметров регрессии построим расчетную таблицу:

N	x	ln(y)	x2	ln(y)2	x∙ln(y)
1	10	3.4012	100	11.5681	34.012
2	20	3.912	400	15.3039	78.2405
3	30	4.2485	900	18.0497	127.4549
4	40	4.4998	1600	20.2483	179.9924
5	50	4.7005	2500	22.0945	235.024
Сумма	150	20.762	5500	87.2646	654.7237

 

Для наших данных система уравнений имеет вид:
или 
Сложив уравнения последней системы, получим:   

Таким образом, получили:   
Уравнение экспоненциальной регрессии:
 
Степенная регрессия. Для расчета параметров регрессии построим расчетную таблицу:

---

N	ln(x)	ln(y)	ln(x)2	ln(y)2	ln(x)∙ln(y)
1	2.3026	3.4012	5.3019	11.5681	7.8315
2	2.9957	3.912	8.9744	15.3039	11.7194
3	3.4012	4.2485	11.5681	18.0497	14.45
4	3.6889	4.4998	13.6078	20.2483	16.5993
5	3.912	4.7005	15.3039	22.0945	18.3884
Сумма	16.3004	20.762	54.7562	87.2646	68.9885

Для наших данных система уравнений имеет вид 
или 
Сложив уравнения последней системы, получим:   

Таким образом, получили:   
Уравнение степенной регрессии:
 
Логарифмическая регрессия. Для расчета параметров регрессии построим расчетную таблицу:

N	ln(x)	y	ln(x)2	y2	ln(x)∙y
1	2.3026	30	5.3019	900	69.0776
2	2.9957	50	8.9744	2500	149.7866
3	3.4012	70	11.5681	4900	238.0838
4	3.6889	90	13.6078	8100	331.9992
5	3.912	110	15.3039	12100	430.3225
Сумма	16.3004	350	54.7562	28500	1219.2697

---

Для наших данных система уравнений имеет вид
 
Решая данную систему уравнений, получили:    Уравнение логарифмической регрессии:
 
Показательная регрессия. Для расчета параметров регрессии построим расчетную таблицу:

N	x	ln(y)	x2	ln(y)2	x∙ln(y)
1	10	3.4012	100	11.5681	34.012
2	20	3.912	400	15.3039	78.2405
3	30	4.2485	900	18.0497	127.4549
4	40	4.4998	1600	20.2483	179.9924
5	50	4.7005	2500	22.0945	235.024
Сумма	150	20.762	5500	87.2646	654.7237

Для наших данных система уравнений имеет вид 
 
Решая данную систему уравнений, получили:   

Уравнение показательной регрессии:  
Задача:

2. 
   Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
   

Таблица 4. Корреляционный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

---

Решение: Вычислим выборочные средние:

 
 
 
Вычислим выборочные дисперсии:
 .   
Вычислим среднее квадратическое отклонение:
 .   
Вычислим коэффициент корреляции:
 
Ответ:   

---

Смотрите также файлы

• Инструкция по оформлению и процедуре защиты.doc

• Методический паспорт проекта.docx

• Суммативное оценивание за раздел Выбор програмного обеспечения.docx

• Мтінмен жмыс. Пернетатада жо символдар.pptx

• 11 сыныпта 4 ашы сабатар ткізілді. Сабаты таырыптары Тарихи ескеткіштер.doc