ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
епенная функция (y=a xb);
1 – b= –1; 2 – b= –0,4; 3 – b= 0; 4 – b= 0,4; 5 – b= 1);
в – экспоненциальная функция (y=a еbx);
1 – b= –0,4; 2 – b= –0,1; 3 – b= 0; 4 – b= 0,1; 5 – b= 1)
Рисунок 1 – Основные виды графиков эмпирических формул
Если график имеет вид кривых, приведенных на рисунке 1в, то можно исп
ользовать выражение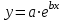
, которое линеаризуется на полулогарифмической сетке в результате замены 
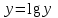, что дает 
.
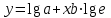При подборе эмпирических формул широко используют полиномы
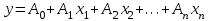, (9)
где А0,…, Аn – постоянные коэффициенты.
Полиномами можно аппроксимировать любые результаты измерений, если он
и графически представляют собой непрерывные функции. Даже при неизвестном выражении (11), ее функции можно определить, применяя методы средни
х и наименьших квадратов.
Метод средних основан на следующем предположении. Если по экспериментальным точкам можно построить несколько плавных кривых, то наилучшей будет та кривая, у которой разностные отклонения наименьшие. Следовательно, подбор эмпирической формулы по методу средних основывается на условии равенства нулю всех отклонений функции от среднего значения, т.е.
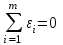, (10)
где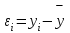
– единичное отклонение.
Последовательность нахождения коэффициентов эмпирической формулы по методу средних сводится к следующему:
а) на основании предварительного анализа результатов эксперимента устанавливают вид функции, в качестве которой чаще всего используют многочлен;
б) определяют число членов ряда, обычно ограничиваясь 3-4;
в) в принятое выражение подставляют все пары измеренных значений хі и уі для определения отклонений
;
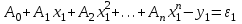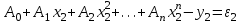; (11)
;
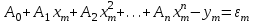г) обычно число уравнений больше количества коэффициентов А, поэтому отклонения распределяют на столько групп, сколько неизвестных коэффициентов в уравнении;
д) приравнивая к нулю сумму отклонений для каждой из групп, получают систему линейных уравнений относительно искомых параметров А. Для решения систем уравнений в математическом обеспечении ПЭВМ имеются стандартные программы;
е) после определения численных значений коэффициентов проверяется качество аппроксимации сопоставлением знаний функции и экспериментальных точек.
Наилучшие результаты при определении параметров заданного уравнения дает использование метода наименьших квадратов. Суть этого метода заключается в следующем. Если все измерения функции у1, у2, ... произведены с одинаковой точностью, а ошибки измерения соответствуют нормальному закону распределения, то параметры исследуемого уравнения определяются из условия, что сумма квадратов отклонений измеренных значений от расчетных принимает наименьшее значение.
Если аппроксимирующее уравнение записать в виде
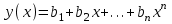, (12)
а имеющиеся данные в точках хiобозначить через уi, то условием минимума суммы квадратов будет равенство
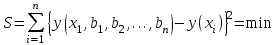, (13)
гдеn– число экспериментальных точек.
Согласно исследованиям фирмы «FIXTURLAZER» в 60% случаях причиной отказа и преждевременного наступления предельного состояния насосного оборудования является значительная вибрация вследствие некачественной центровки и недопустимого значения параллельной и угловой расцентровки валов, а для машинного оборудования доля отказов по этой причине достигает 49%.
Проведенные эмпирические (экспериментальные) исследования позволили установить функциональные зависимости СКЗ виброскорости насосных агрегатов от величины параллельной (S, мм) и угловой (α, град) расцентровки валов. При этом методом наименьших квадратов были получены эмпирические формулы, дающие аналитическое выражение функциональной зависимости между исследуемыми величинами:
V = f(S, α ) (14)
где V – СКЗ виброскорости, мм/с; S – величины параллельной расцентровки, мм; α – величины угловой расцентровки, град.
Согласно методу, вид аппроксимации и коэффициенты эмпирической формулы определяются в зависимости от суммы квадратов отклонений экспериментальных значений (VЭ1, VЭ2…VЭn) от расчетных (VР1, VР2…VРn), которое должно быть минимальным:
S = Σ( VЭn - VРn)2 (15)
Геометрически задача сводится к построению по эмпирической формуле кривой, расположенной максимально близко к опытным результатам. Линия тренда позволяет графически отобразить тенденцию данных и прогнозировать их дальнейшее изменение. Подобный анализ называется также регрессионным анализом.
Степень близости линии тренда к практическим точкам полученных результатов определяется величиной достоверности (точности) аппроксимации R, который также имеет название коэффициент детерминации. Расчет коэффициента детерминации производится по формуле:
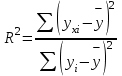, (16)
где yxi – значения результатов эмпирических замеров;
yi – значения результатов теоретической (аппроксимированной) кривой;
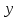– математическое ожидание.
Линия тренда наиболее соответствует действительности, когда значение R2 стремится к единице.
Для расчетов воспользуемся таблицей 4.
Таблица 4 - Экспериментальные данные замеров для насосного агрегата марки ВВН-12М (зав. № 3562)
Результаты расчетов представлены на рисунках 2, 3 и 4.
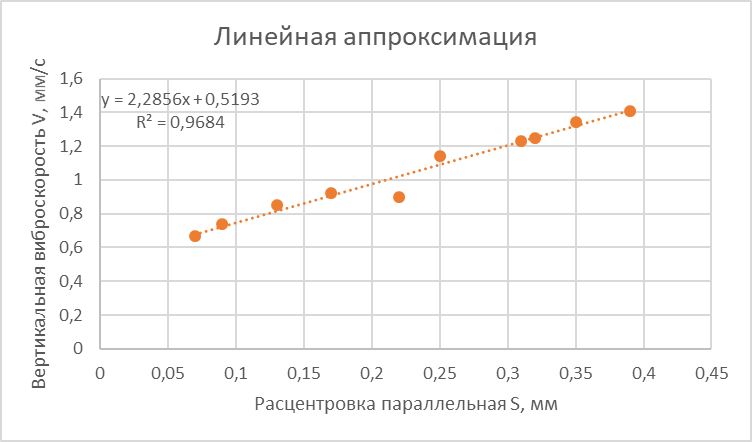
Рисунок 2 – Линейная аппроксимация
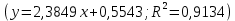
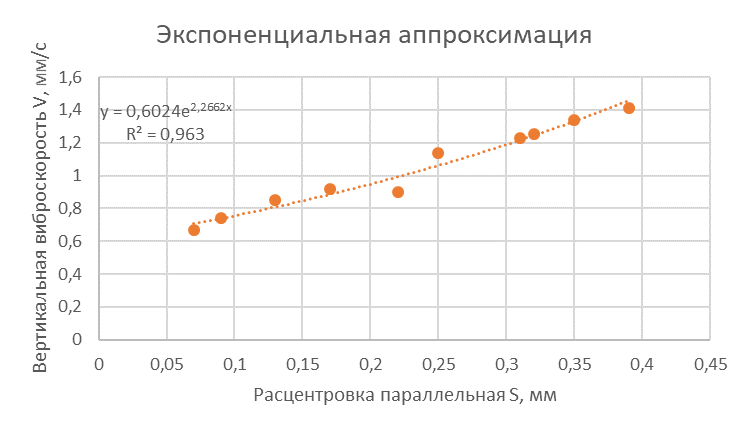
Рисунок 3 – Экспоненциальная аппроксимация
)
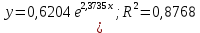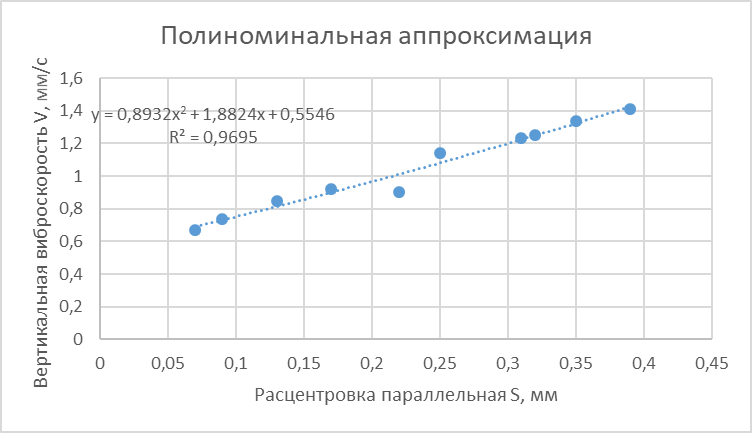
Рисунок 4 – Полиноминальная аппроксимация
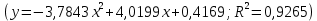
Заключение
Подводя итоги данной курсовой работы, можно сказать, что все поставленные задачи были выполнены, цели достигнуты
В процессе выполнения курсовой работы я закрепил материал, полученный во время лекционных, лабораторных и практических занятий, были рассмотрены методы обработки и анализа экспериментальных данных на этапе проектирования, также я приобрел новые навыки в работе со справочной литературой и стандартами в сфере насосного и компрессорного оборудования.
Список литературы
1. СТП 005 - 2007. Стандарт предприятия. Дипломное проектирование. Оформление расчетно-пояснительной записки и графической части / «Воронежский государственный технический университет». Воронеж, 2007. 34 с.
2. Основы научных исследований: учебник для техн. вузов / В.И. Крутов, И.М. Грушко, В.В. Попов и др.; под ред. В.И. Крутова, В.В. Попова. - М.: Высш. шк., 1989. - 400 с.
3. Основы научных исследований: курс лекций: учеб. пособие / С.Г. Валюхов, В.В. Бородкин, Ю.А. Булыгин, С.А. Повеквечных; ФГБОУ ВПО «Воронежский государственный технический университет». - Воронеж: Издательско-полиграфический центр «Научная книга», 2012. - 238 с.
4. Методы и средства регистрации параметров энергетического оборудования газонефтепроводов / С.Г. Валюхов, В.В. Бородкин, Ю.А. Булыгин; ФГБОУ ВО «Воронежский государственный технический университет». – Воронеж: Издательско-полиграфический центр «Научная книга», 2016.- 194 с.
5. Шкляр М.Ф. Основы научных исследований: учеб. пособие. - М.: ИТК «Дашков и К°», 2008. - 244 с.
6. Зайдель А.М. Ошибки измерений физических величин / А.М. Зайдель. - Л.: Наука, 1974. - 108 с.
7. Савчук В.П. Обработка результатов измерений. Физическая лаборатория: учеб. пособие для студентов вузов / В.П. Савчук. - Одесса: ОНПУ, 2002. - Ч.1. - 54 с.
8. Львовский Е.Н. Статистические методы построения эмпирических формул / Е.Н. Львовский. - М.: Высш школа, 1982. - 224 с.
9. Румшинский Л.З. Математическая обработка результатов эксперимента / Л.З.Румшинский. - М.: Наука, 1971. - 192 с.
ПРИЛОЖЕНИЕ А
Величина гарантийного коэффициента t в зависимости
от значения доверительной вероятности
1 – b= –1; 2 – b= –0,4; 3 – b= 0; 4 – b= 0,4; 5 – b= 1);
в – экспоненциальная функция (y=a еbx);
1 – b= –0,4; 2 – b= –0,1; 3 – b= 0; 4 – b= 0,1; 5 – b= 1)
Рисунок 1 – Основные виды графиков эмпирических формул
Если график имеет вид кривых, приведенных на рисунке 1в, то можно исп
ользовать выражение
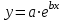, которое линеаризуется на полулогарифмической сетке в результате замены 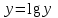, что дает 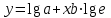.При подборе эмпирических формул широко используют полиномы
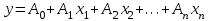, (9)где А0,…, Аn – постоянные коэффициенты.
Полиномами можно аппроксимировать любые результаты измерений, если он
и графически представляют собой непрерывные функции. Даже при неизвестном выражении (11), ее функции можно определить, применяя методы средни
х и наименьших квадратов.
Метод средних основан на следующем предположении. Если по экспериментальным точкам можно построить несколько плавных кривых, то наилучшей будет та кривая, у которой разностные отклонения наименьшие. Следовательно, подбор эмпирической формулы по методу средних основывается на условии равенства нулю всех отклонений функции от среднего значения, т.е.
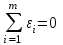, (10)где
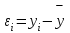– единичное отклонение.Последовательность нахождения коэффициентов эмпирической формулы по методу средних сводится к следующему:
а) на основании предварительного анализа результатов эксперимента устанавливают вид функции, в качестве которой чаще всего используют многочлен;
б) определяют число членов ряда, обычно ограничиваясь 3-4;
в) в принятое выражение подставляют все пары измеренных значений хі и уі для определения отклонений
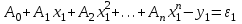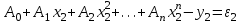; ; (11) 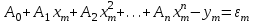;г) обычно число уравнений больше количества коэффициентов А, поэтому отклонения распределяют на столько групп, сколько неизвестных коэффициентов в уравнении;
д) приравнивая к нулю сумму отклонений для каждой из групп, получают систему линейных уравнений относительно искомых параметров А. Для решения систем уравнений в математическом обеспечении ПЭВМ имеются стандартные программы;
е) после определения численных значений коэффициентов проверяется качество аппроксимации сопоставлением знаний функции и экспериментальных точек.
Если аппроксимирующее уравнение записать в виде
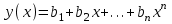, (12)а имеющиеся данные в точках хiобозначить через уi, то условием минимума суммы квадратов будет равенство
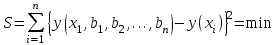, (13)гдеn– число экспериментальных точек.
Согласно исследованиям фирмы «FIXTURLAZER» в 60% случаях причиной отказа и преждевременного наступления предельного состояния насосного оборудования является значительная вибрация вследствие некачественной центровки и недопустимого значения параллельной и угловой расцентровки валов, а для машинного оборудования доля отказов по этой причине достигает 49%.
Проведенные эмпирические (экспериментальные) исследования позволили установить функциональные зависимости СКЗ виброскорости насосных агрегатов от величины параллельной (S, мм) и угловой (α, град) расцентровки валов. При этом методом наименьших квадратов были получены эмпирические формулы, дающие аналитическое выражение функциональной зависимости между исследуемыми величинами:
V = f(S, α ) (14)
где V – СКЗ виброскорости, мм/с; S – величины параллельной расцентровки, мм; α – величины угловой расцентровки, град.
Согласно методу, вид аппроксимации и коэффициенты эмпирической формулы определяются в зависимости от суммы квадратов отклонений экспериментальных значений (VЭ1, VЭ2…VЭn) от расчетных (VР1, VР2…VРn), которое должно быть минимальным:
S = Σ( VЭn - VРn)2 (15)
Геометрически задача сводится к построению по эмпирической формуле кривой, расположенной максимально близко к опытным результатам. Линия тренда позволяет графически отобразить тенденцию данных и прогнозировать их дальнейшее изменение. Подобный анализ называется также регрессионным анализом.
Степень близости линии тренда к практическим точкам полученных результатов определяется величиной достоверности (точности) аппроксимации R, который также имеет название коэффициент детерминации. Расчет коэффициента детерминации производится по формуле:
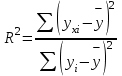, (16)где yxi – значения результатов эмпирических замеров;
yi – значения результатов теоретической (аппроксимированной) кривой;
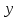– математическое ожидание.Линия тренда наиболее соответствует действительности, когда значение R2 стремится к единице.
Для расчетов воспользуемся таблицей 4.
Таблица 4 - Экспериментальные данные замеров для насосного агрегата марки ВВН-12М (зав. № 3562)
| № | S, мм | Вертикальная виброскорость V мм/с |
| 1 | 0,07 | 0,66 |
| 2 | 0,09 | 0,68 |
| 3 | 0,12 | 0,95 |
| 4 | 0,16 | 1,03 |
| 5 | 0,2 | 0,97 |
| 6 | 0,25 | 1,25 |
| 7 | 0,3 | 1,22 |
| 8 | 0,31 | 1,23 |
| 9 | 0,33 | 1,39 |
| 10 | 0,37 | 1,41 |
Результаты расчетов представлены на рисунках 2, 3 и 4.
Рисунок 2 – Линейная аппроксимация
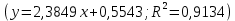
Рисунок 3 – Экспоненциальная аппроксимация
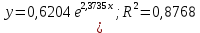) Рисунок 4 – Полиноминальная аппроксимация
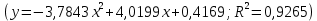
Заключение
Подводя итоги данной курсовой работы, можно сказать, что все поставленные задачи были выполнены, цели достигнуты
В процессе выполнения курсовой работы я закрепил материал, полученный во время лекционных, лабораторных и практических занятий, были рассмотрены методы обработки и анализа экспериментальных данных на этапе проектирования, также я приобрел новые навыки в работе со справочной литературой и стандартами в сфере насосного и компрессорного оборудования.
Список литературы
1. СТП 005 - 2007. Стандарт предприятия. Дипломное проектирование. Оформление расчетно-пояснительной записки и графической части / «Воронежский государственный технический университет». Воронеж, 2007. 34 с.
2. Основы научных исследований: учебник для техн. вузов / В.И. Крутов, И.М. Грушко, В.В. Попов и др.; под ред. В.И. Крутова, В.В. Попова. - М.: Высш. шк., 1989. - 400 с.
3. Основы научных исследований: курс лекций: учеб. пособие / С.Г. Валюхов, В.В. Бородкин, Ю.А. Булыгин, С.А. Повеквечных; ФГБОУ ВПО «Воронежский государственный технический университет». - Воронеж: Издательско-полиграфический центр «Научная книга», 2012. - 238 с.
4. Методы и средства регистрации параметров энергетического оборудования газонефтепроводов / С.Г. Валюхов, В.В. Бородкин, Ю.А. Булыгин; ФГБОУ ВО «Воронежский государственный технический университет». – Воронеж: Издательско-полиграфический центр «Научная книга», 2016.- 194 с.
5. Шкляр М.Ф. Основы научных исследований: учеб. пособие. - М.: ИТК «Дашков и К°», 2008. - 244 с.
6. Зайдель А.М. Ошибки измерений физических величин / А.М. Зайдель. - Л.: Наука, 1974. - 108 с.
7. Савчук В.П. Обработка результатов измерений. Физическая лаборатория: учеб. пособие для студентов вузов / В.П. Савчук. - Одесса: ОНПУ, 2002. - Ч.1. - 54 с.
8. Львовский Е.Н. Статистические методы построения эмпирических формул / Е.Н. Львовский. - М.: Высш школа, 1982. - 224 с.
9. Румшинский Л.З. Математическая обработка результатов эксперимента / Л.З.Румшинский. - М.: Наука, 1971. - 192 с.
ПРИЛОЖЕНИЕ А
Величина гарантийного коэффициента t в зависимости
от значения доверительной вероятности