Файл: Задача Определить производительность спаренной вальцовой дробилки для измельчения ячменя, если длина валков l 0,6 м, ширина зазора между ними b 0,001 м, средняя скорость вращения валков мс, объемная масса ячменя 700 кгм.docx
Добавлен: 11.12.2023
Просмотров: 72
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример
Дано: Рассчитать расход воздуха на сушку 2000 кг сахара-песка, если известно, что t0 = 15 °С; φ0 = 40%; t2 =45 °С; φ2 = 45 %. Влажность сахара-песка до сушки W1 = 3,5 %; после сушки W2 = 0,14 %.
Решение:
Количество влаги, удаляемой из сахара при сушке, определяется по формуле
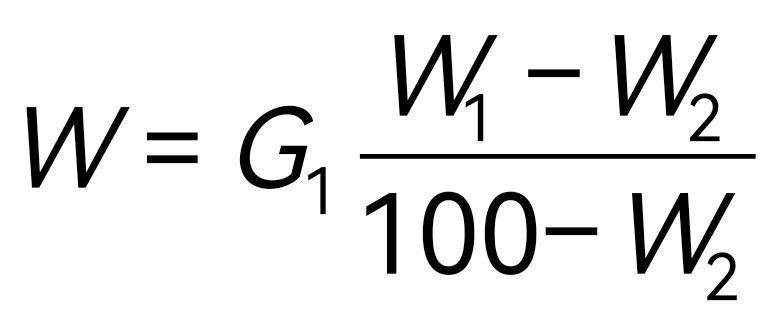
W = 2000 (3,5 – 0,14)/ (100-0,14) = 67,3 кг.
По i-d диаграмме находим влагосодержание воздуха до сушки и после нее: х0 = 0,004 кг/кг сухого воздуха; х2 = 0,0183 кг/кг сухого воздуха.
Расход воздуха на испарение 1 кг влаги определяем по формуле
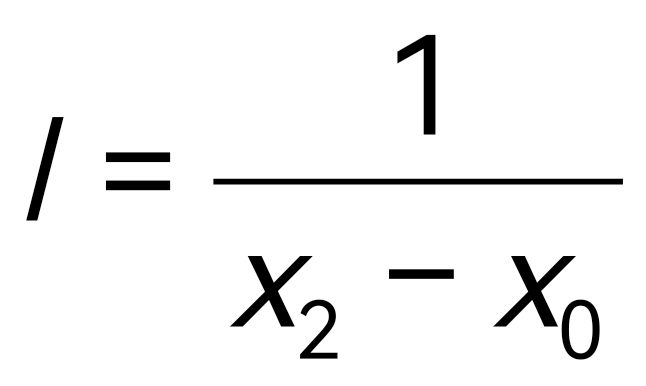
l = 1000 / (18,3 – 4,0) = 70 кг сухого воздуха.
Количество воздуха, которое потребуется на испарение 67,3 кг влаги определяем по формуле
L = l·W
L = 70·67,3 = 4710,6 кг.
ЗАДАНИЕ 5
Задача 1. Определить аналитическим путем число теоретических и действительных тарелок в нижней части исчерпывающей колонны, если содержание легко летучего компонента в жидкости изменяется от 0,2 до 0,004 мол %, отношение G/L = 0,174, коэффициент испарения легко летучего компонента К = 13. Средний КПД тарелки η = 0,5.
Пример.
-
Число теоретических тарелок определяется по формуле
где xn и xR – содержание легколетучего компонента в жидкости на n-тарелке и в остатке, мол %;
К – коэффициент испарения легколетучего компонента в пределах указанных концентрацией его жидкости (для водно-спиртовой жидкости можно принять К = 13);
G и L – величины парового и жидкостного потоков в колонне, кг/с.
nT = (lg(1+(0,20·0,04) (13·0,174 – 1) lg(13·0,174)) – 1 = 3,32.
2. Действительное число тарелок определяется по формуле

nД = 3,32/0,5 = 6,64.
Принимаем 7 тарелок.
Таблица 9.2 – Индивидуальные задания
| Последняя цифра шифра | xn , мол % | xR , мол % | Предпоследняя цифра шифра | η | G/L |
| 0 | 0,17 | 0,005 | 0 | 0,45 | 0,16 |
| 1 | 0,18 | 0,005 | 1 | 0,46 | 0,162 |
| 2 | 0,19 | 0,004 | 2 | 0,48 | 0,165 |
| 3 | 0,2 | 0,004 | 3 | 0,6 | 0,168 |
| 4 | 0,21 | 0,004 | 4 | 0,62 | 0,17 |
| 5 | 0,22 | 0,004 | 5 | 0,5 | 0,172 |
| 6 | 0,23 | 0,005 | 6 | 0,52 | 0,174 |
| 7 | 0,24 | 0,005 | 7 | 0,54 | 0,178 |
| 8 | 0,25 | 0,004 | 8 | 0,58 | 0,18 |
| 9 | 0,26 | 0,004 | 9 | 0,47 | 0,182 |