характеризует колеблемость групповых или частных средних ( _i) около общей средней (x_i) и исчисляется по формулам:

;

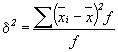
где x_i - средняя по каждой отдельной группе;

- средняя по всей совокупности;

n - число единиц совокупности;

f - частоты или веса.

Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней.

Она характеризует систематическую вариацию, которая возникает под влиянием фактора признака, положенного в основу группировки.

Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем среднюю из внутригрупповых дисперсий.

Средняя из внутригрупповых дисперсий характеризует случайную вариацию, которая возникает по влиянием всех факторов, кроме положенного в основание группировки.

Чтобы определить её, надо рассчитать вначале внутригруппировочные дисперсии по каждой группе в отдельности, а затем среднюю их них.

Средне квадратическое отклонение.

Средне квадратическое отклонение (σ) и дисперсия (σ²) определяются так:

Для несгруппированных данных (первичного ряда)

σ ⁼ _; σ^{2 =}

_{для вариационного ряда}

σ ⁼ σ^{2 =}

формула для расчета дисперсии может быть преобразована:

σ^{2 =}

---

^{= = =
=} - <sub>,

т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно,</sub>

σ^{2 =} -

Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойствами мажорантности средних.

---

Смотрите также файлы

• Задание 27 и 34. Задачи на растворимость веществ. Расчёты с использованием понятий растворимость, массовая доля вещества в растворе.docx

• Протокол от 20 г председатель пцк е. В. Симонова Утверждаю Зам директора по У. Р.docx

• Ответ Уменьшается.docx

• Что способствует сохранению и укреплению здоровья.pptx

• Теcт прогрaммы в cреде ms dos.docx