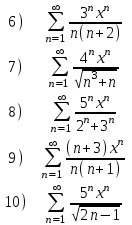Файл: Функционалды атарлар 7. атарды жинатылы облысын табыыз Шешуі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФУНКЦИОНАЛДЫҚ ҚАТАРЛАР
№7. Қатардың жинақтылық облысын табыңыз
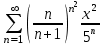
Шешуі: Қатардың жинақтылық облысын табу үшін Коши белгісін қолданамыз.
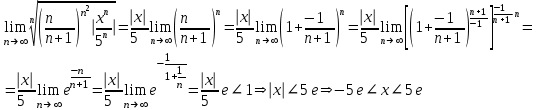
Жинақталу облысының шекараларында жинақтылыққа зерттейміз, яғни
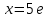және 
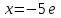нүктелерінде. 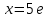болғанда 
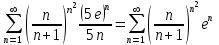сандық қатарды аламыз. Бұл қатарға Даламбер белгісін қолданамыз: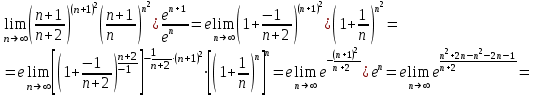 
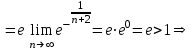қатар жинақты. 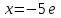болғанда 
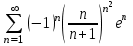таңбасы ауыспалы қатарды аламыз 
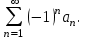Лейбниц белгісін қолданып, 
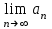табамыз: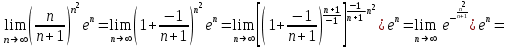
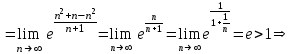қатар жинақты. Жауабы: Берілген қатардың жинақтылық облысы:
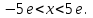
№8. Қатардың жинақтылық облысын табыңыз
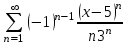
Шешуі: Даламбер формуласын қолданамыз
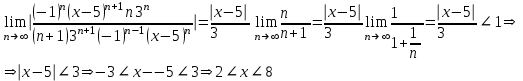
х = 2 болғанда
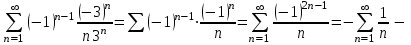гармониялық қатар жинақсыз. х = 8 болғанда 
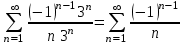- таңбасы ауыспалы қатар, Лейбниц белгісі бойынша: 1) 
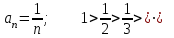- кемімелі тізбек. 2) 
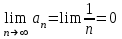. Сонымен, 
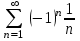қатары шартты жинақты, өйткені абсолют шамадан құрылған қатар жинақсыз, яғни х = 8 
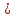болғанда қатар жинақты.
Жауабы: 2 < х ≤ 8.
№9. Дәрежелік қатардың жинақтылық интервалын табыңыз
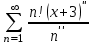.Шешуі: Даламбер белгісін қолданамыз
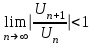
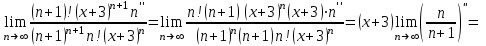
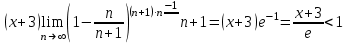
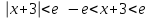
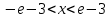.Жауабы:
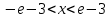.№10. Қатардың қосындысын табыңыз
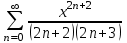.Шешуі:
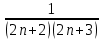бөлшегін келесі түрде жіктейміз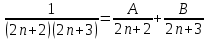 
.
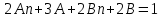
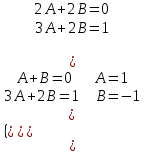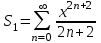және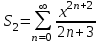 
қосындыларын қарастырайық. 
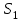қосындыны келесідей жазамыз 
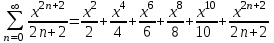. Мүшелеп дифференциалдау арқылы 
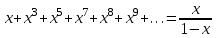аламыз. Соңғы өрнек геометриялық прогрессия, мұндағы 
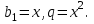Онда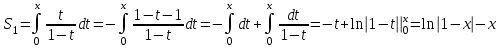 
. Енді 
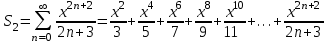қарастырайық. Мүшелеп 
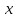-ке көбейтіп 
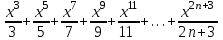аламыз, мүшелеп дифференциалдап 
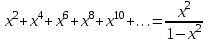аламыз. Бұл геометриялық прогрессия. Сонымен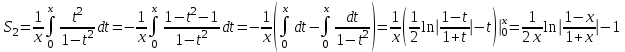 
Нәтижесінде, берілген қатардың қосындысы
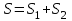
Жауабы:
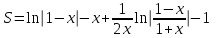
№11. Қатардың қосындысын табыңыз
.
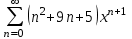
Шешуі: Біріншіден Даламбер белгісі бойынша қатардың жинақтылық облысын табу керек. Берілген қатардың жинақтылық облысы (-1; 1). Бұл қатарды келесі түрде жіктейміз
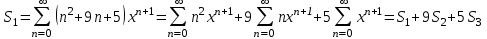. Алдымен 
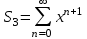қарастырамыз және оны 
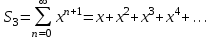жіктейміз. Бұл геометриялық прогрессия, мұндағы 
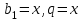, яғни 
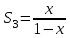. Енді 
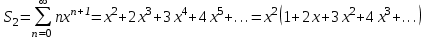қарастырамыз. Жақшадағы өрнекті мүшелеп интегралдаймыз, 
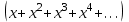- бұл геометриялық прогрессия, мұндағы 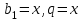онда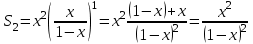 
. Енді 
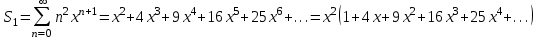қарастырамыз. Жақшадағы өрнекті мүшелеп интегралдаймыз 
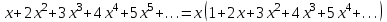. Тағы да жақшадағы өрнекті мүшелеп интегралдап 
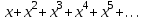аламыз, бұл да геометриялық прогрессия, мұндағы 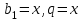. Сонымен,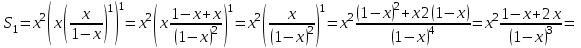
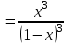. Енді қатардың қосындысын табайық 
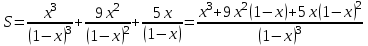.№12. Қатардың көмегімен интегралды есептеціз
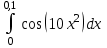.Шешуі: Функцияны қатарға жіктеу формуласын қолданамыз
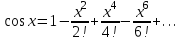
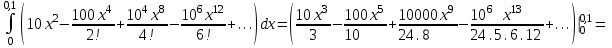
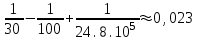
Дәрежелік қатардың жинақтылық облысын анықтаңыз.
