ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 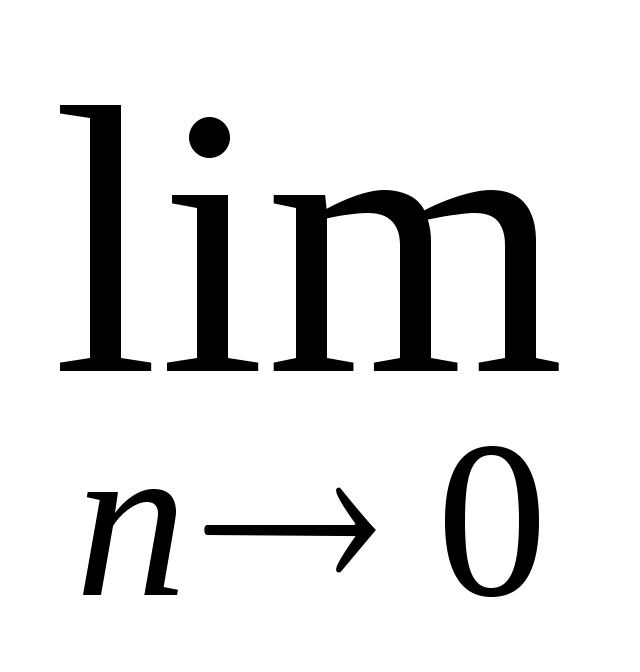
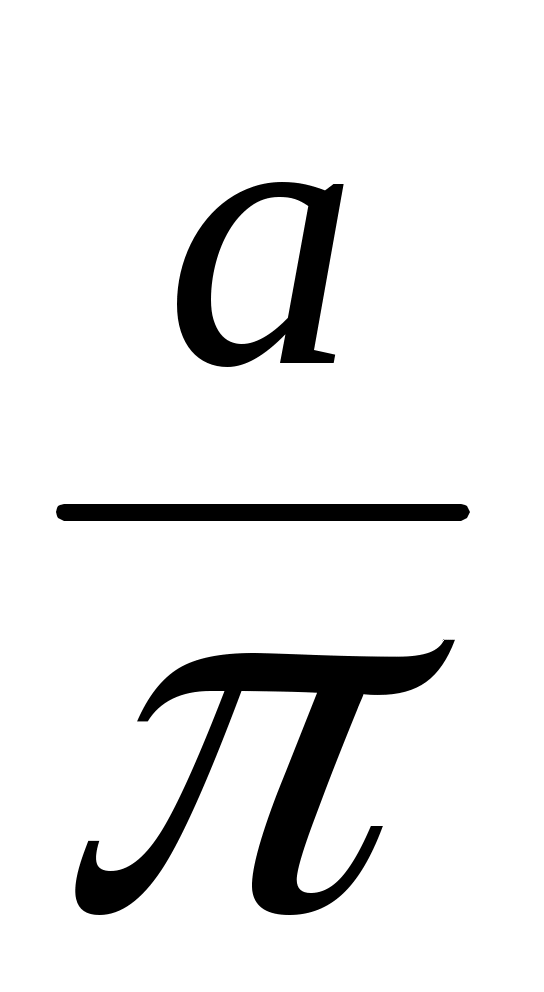
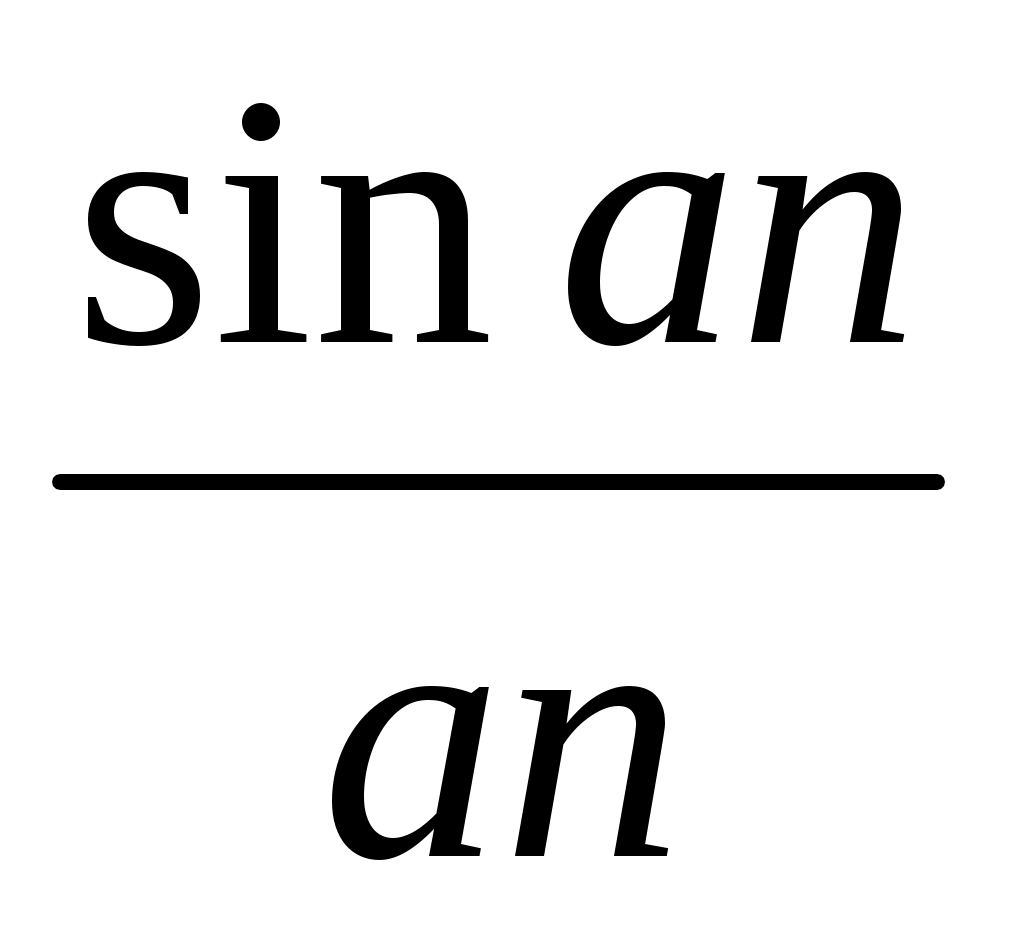 =
=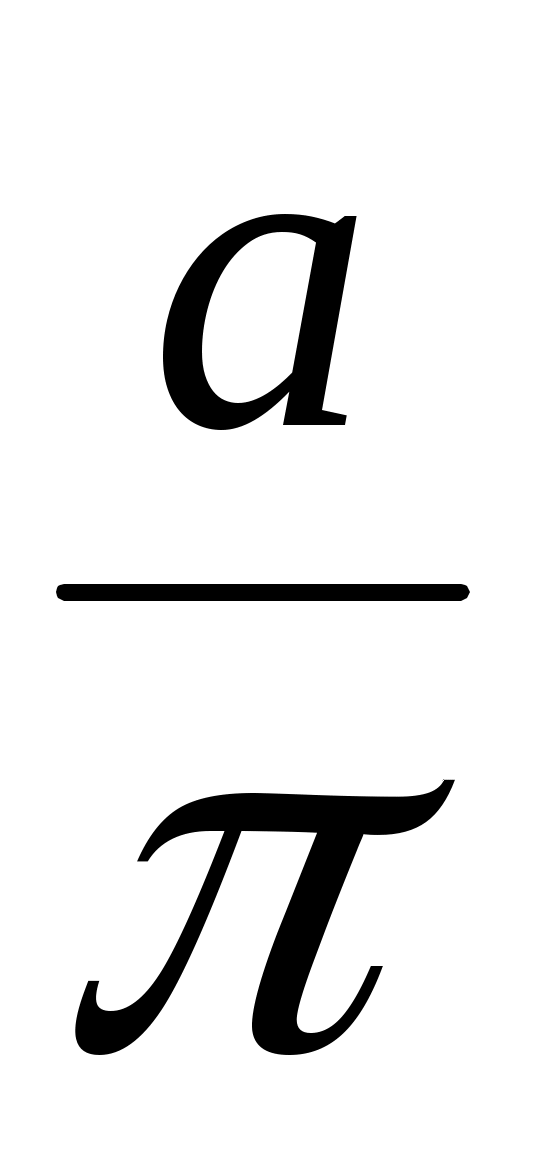

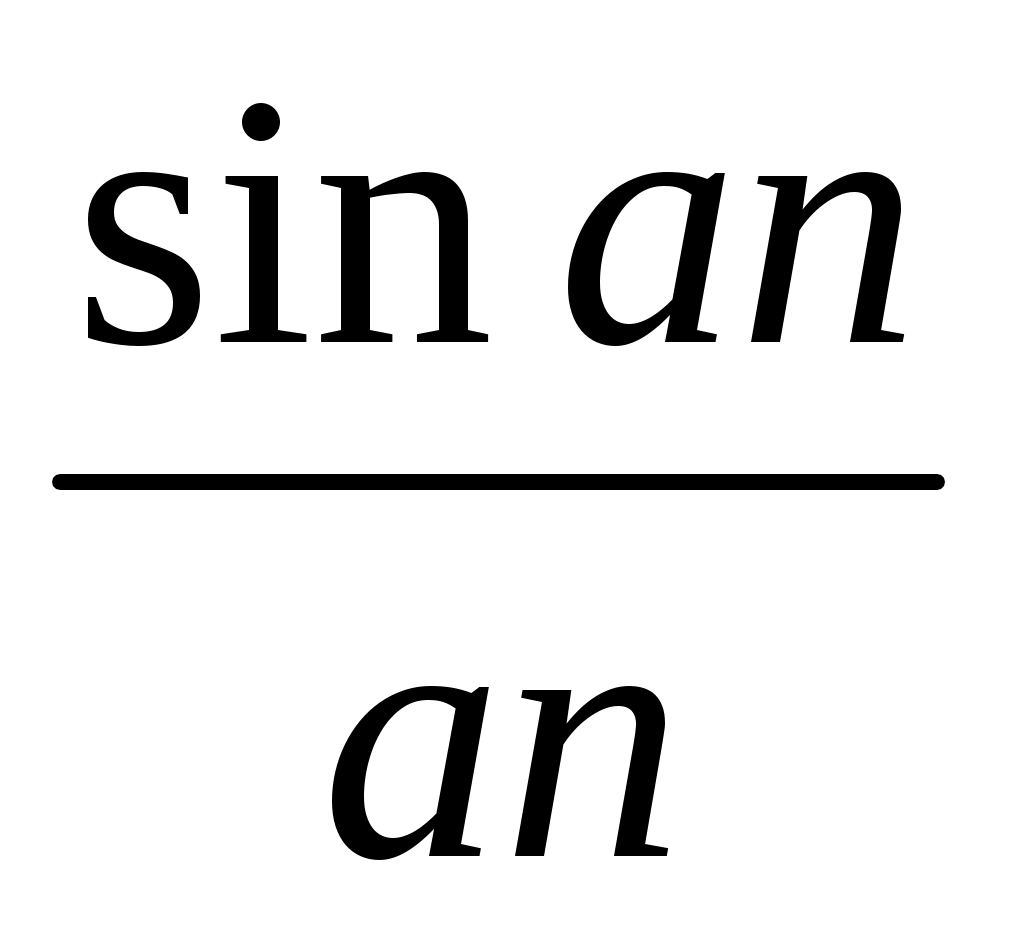 =
= 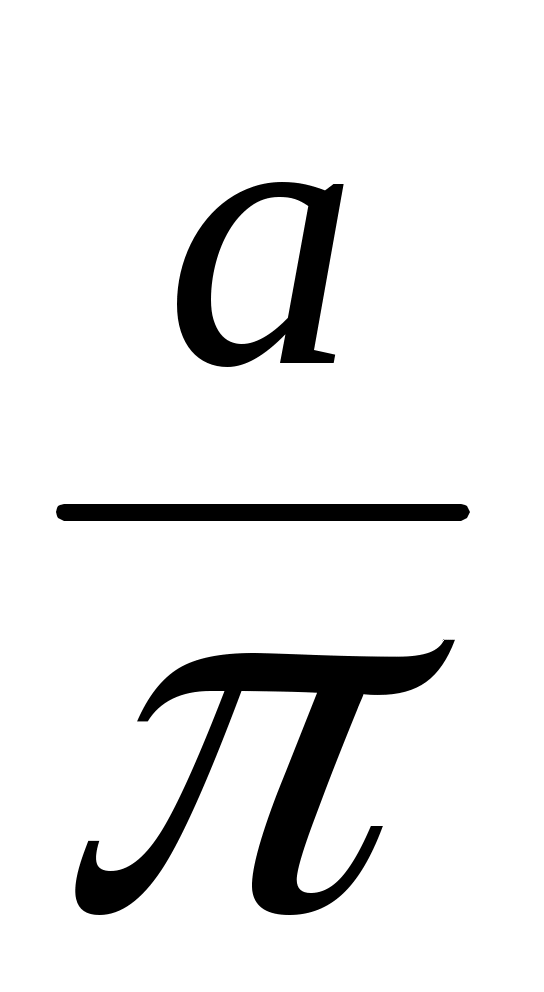 ,
,
bn = =
=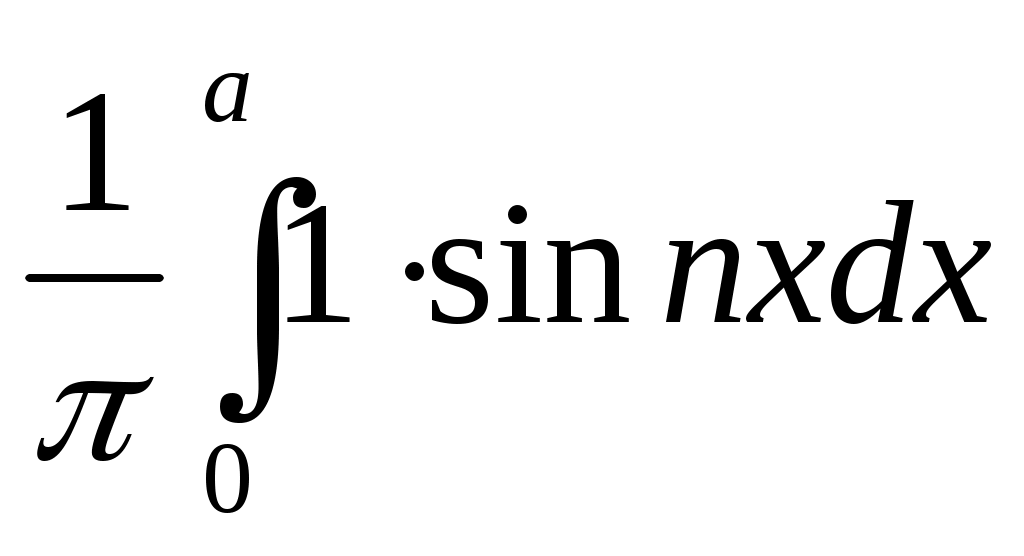 = –
= –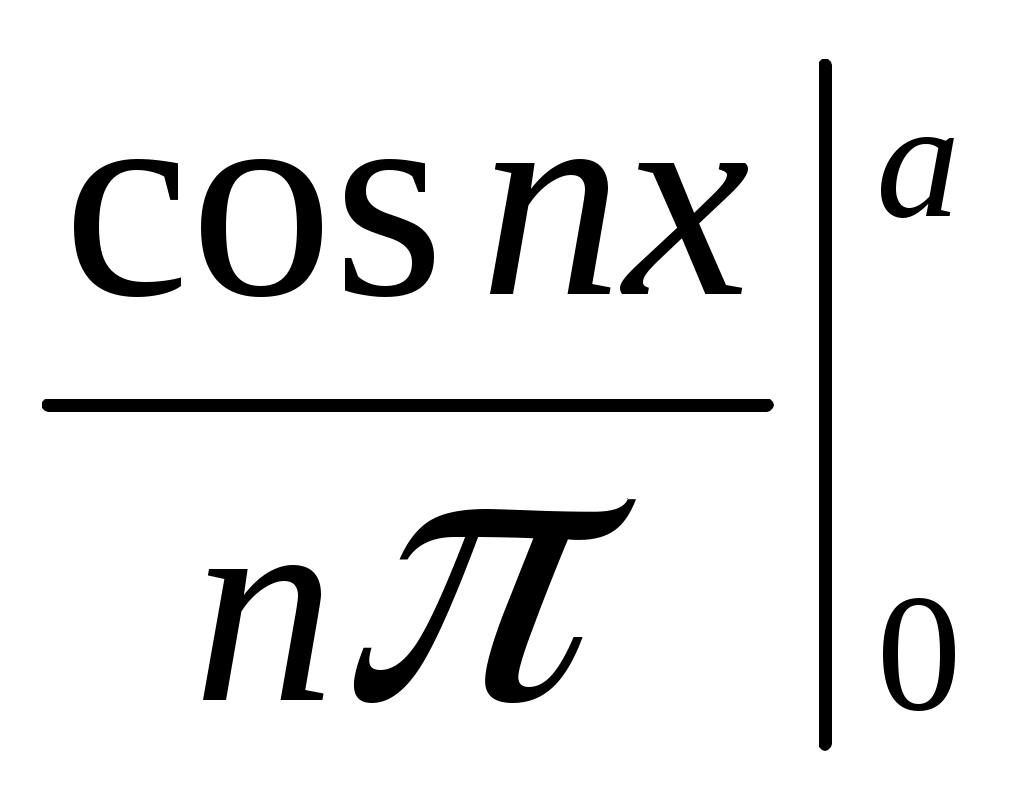 = –
= –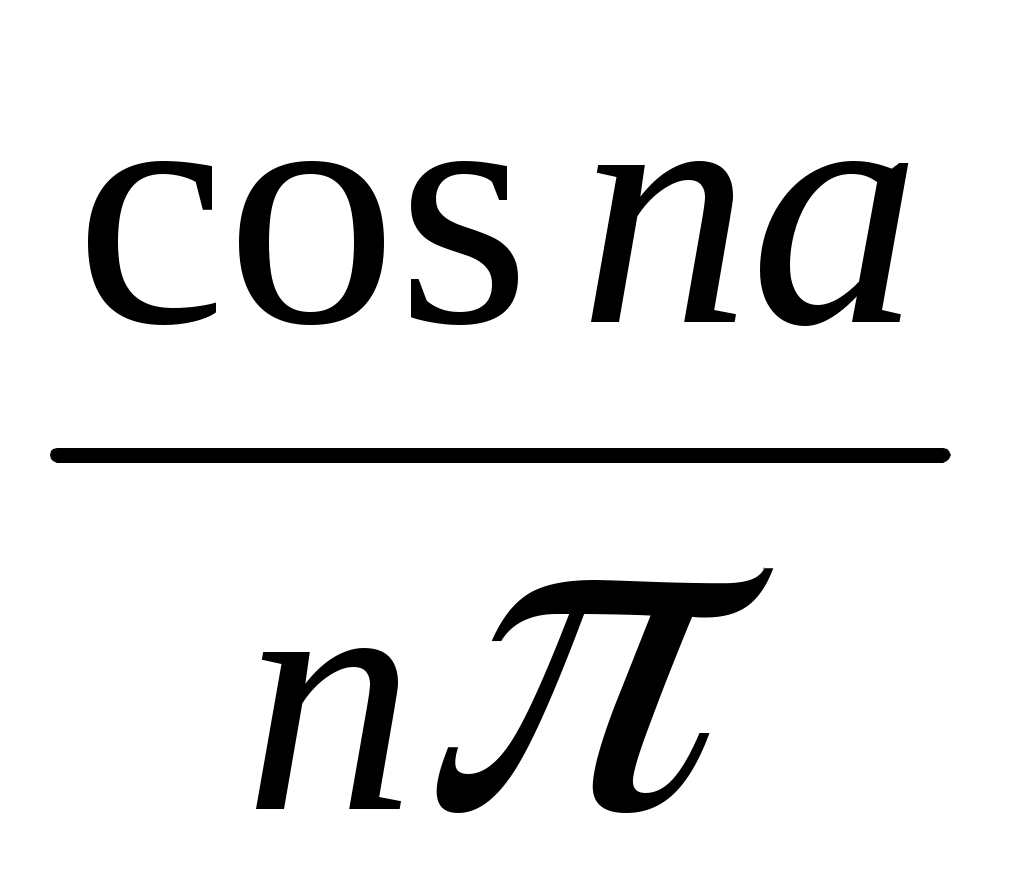 +
+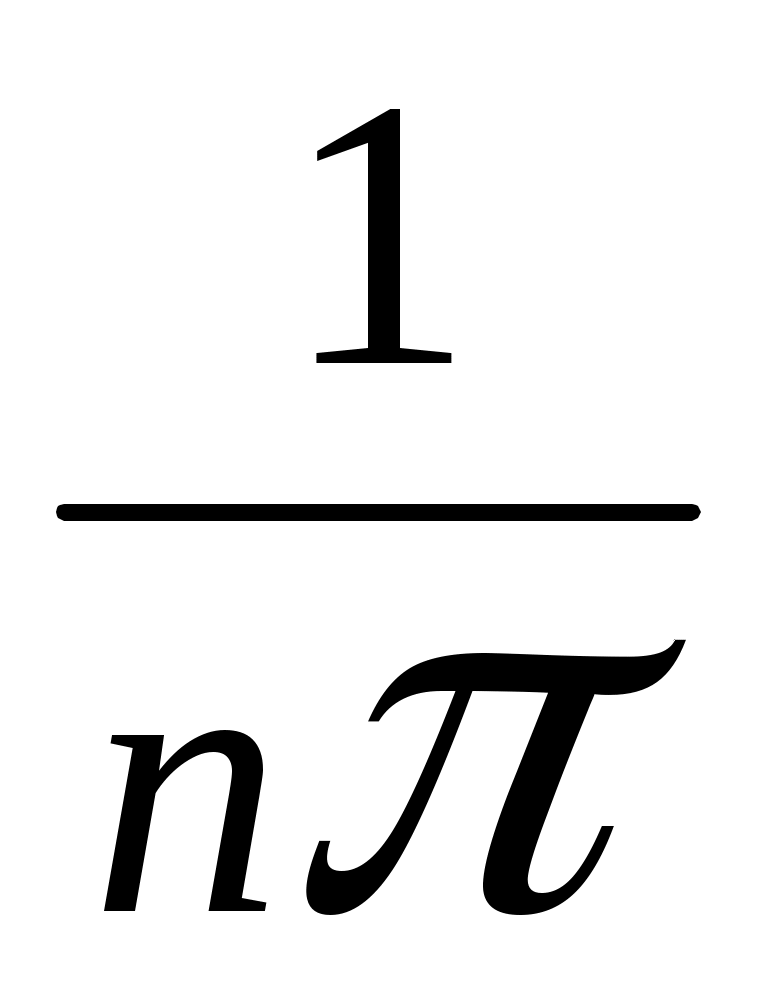 =
=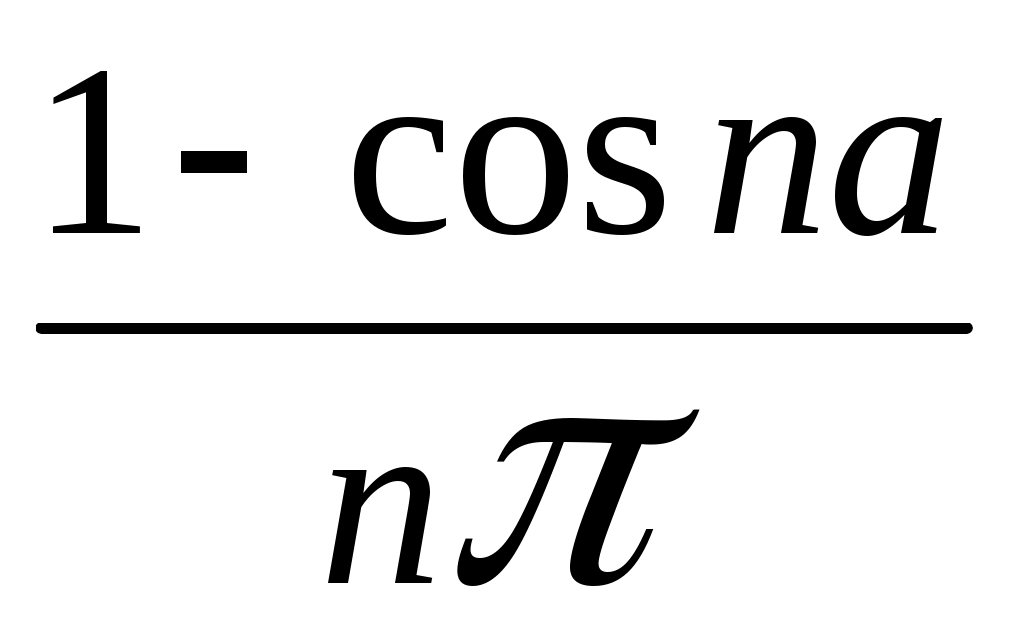 , при n 0.
, при n 0.
Следовательно,
f(x) =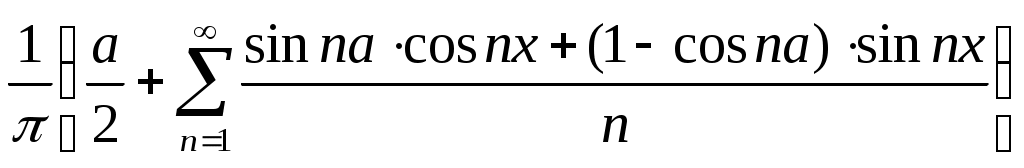 .
.
В интервале [-; ] ряд сходится к функции f(x), в точках х = к 0: ( 1/2 [ f(–+0) + f(–0)] = 0 ), в точках х = a, x= 0 к 1/2 : ( 1/2 [ f(х-0) + f(х+0)] = =1/2 ).
Ряд Фурье в виде простых гармоник. Спектры.
Практически любую периодическую функцию можно разложить на простые гармоники с помощью тригонометрического ряда (ряда Фурье):
f(x) =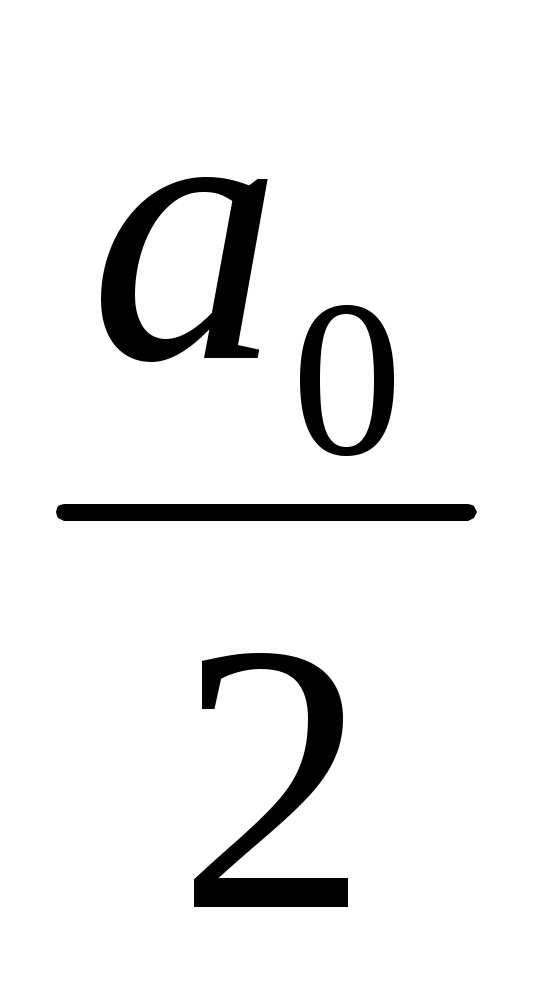 +
+ 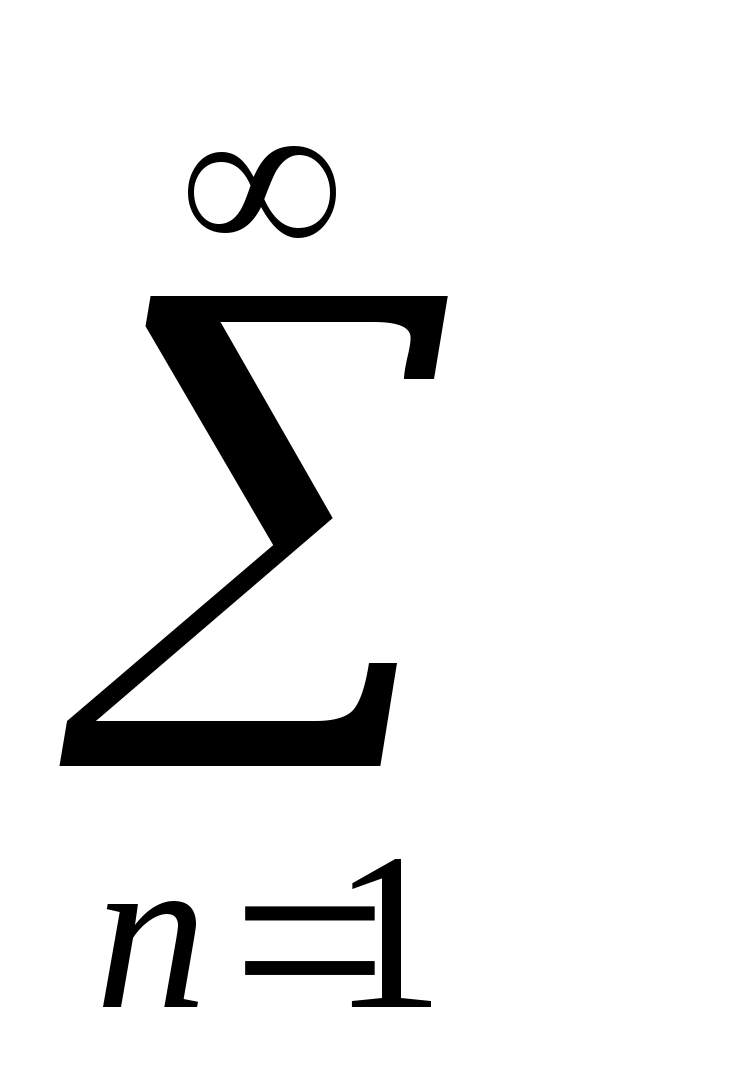 ( ancos nx + bnsin nx ), (*)
( ancos nx + bnsin nx ), (*)
Запишем данный ряд в виде суммы простых гармоник, полагая коэффициенты равными an= Ansinn, bn= Ancosn . Получим: ancos n + bnsinn = Ansin( nx+ n ), где
An =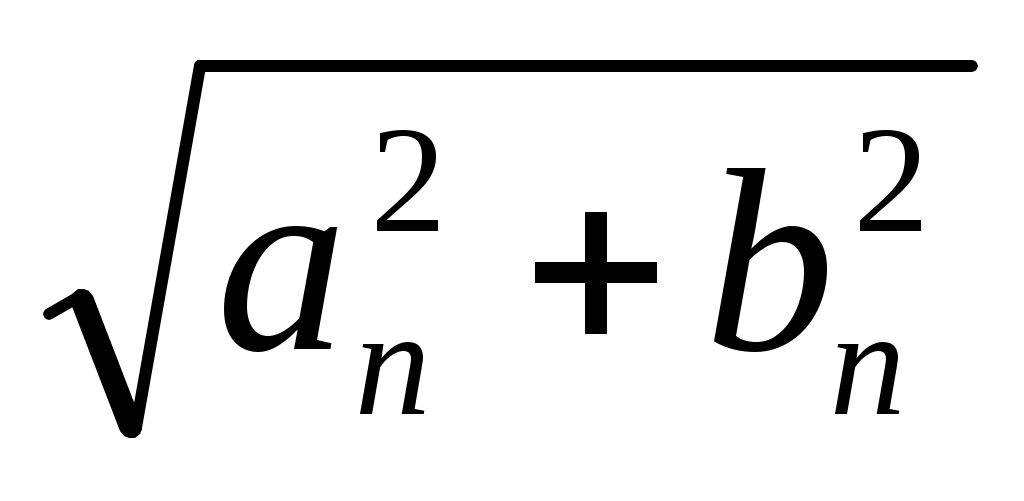 , tg n =
, tg n = 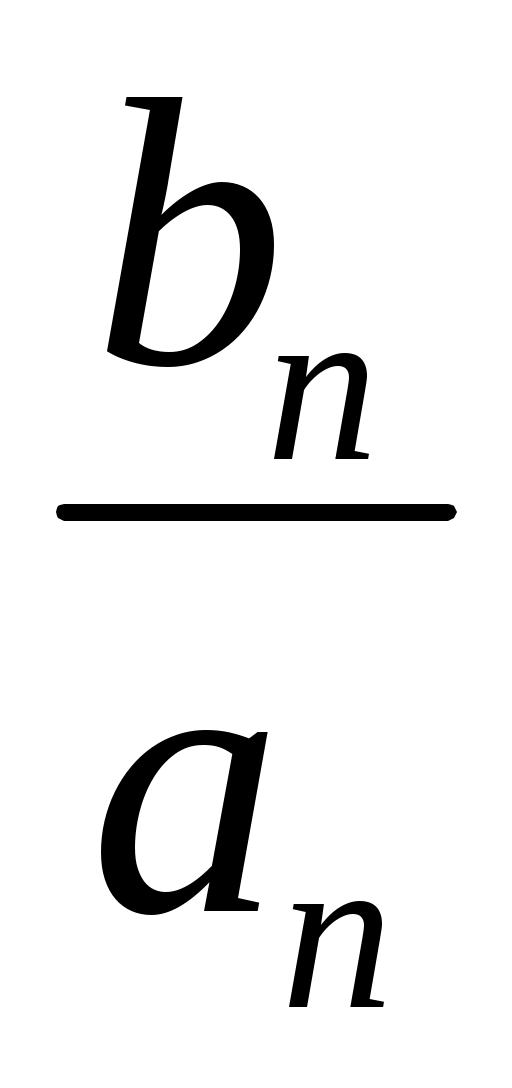 . (**)
. (**)
Тогда ряд (*) в виде простых гармоник примет вид
f(x) =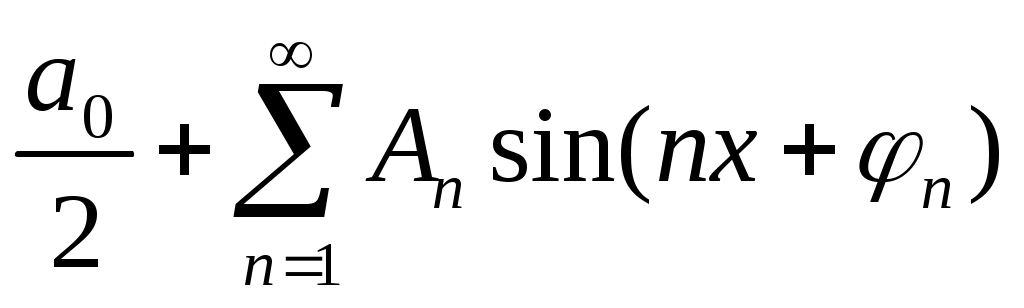 .
.
Ряд Фурье представляет периодическую функцию суммой хотя и бесконечного числа синусоид, но с частотами, имеющими определенное дискретное значение.
Иногда n-ую гармонику записывают в виде ancos nx + bnsin nx = Ancos(nx – n) , где an= Ancosn , bn= An sinn .
При этом An и n определяются по формулам (**). Тогда ряд (*) примет вид
f(x) =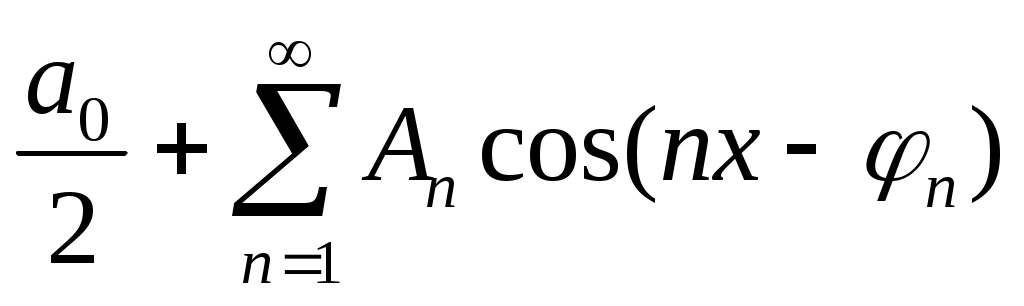 .
.
Определение 9. Операция представления периодической функции f(x) рядом Фурье называется гармоническим анализом.
Выражение (*) встречается и в другой, более употребительной форме:
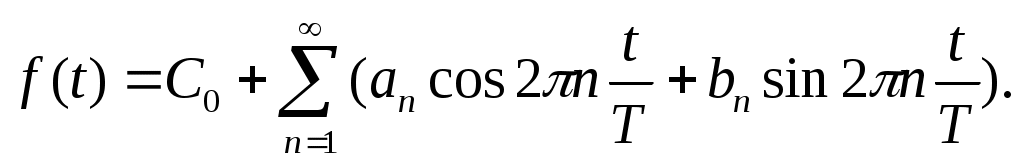
Коэффициенты an, bn определяются по формулам:
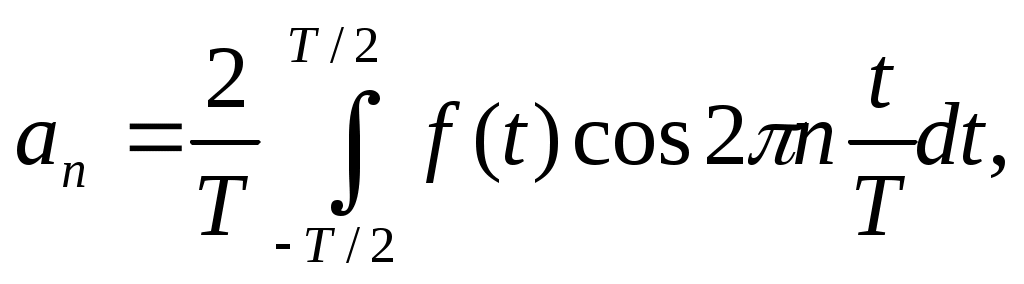
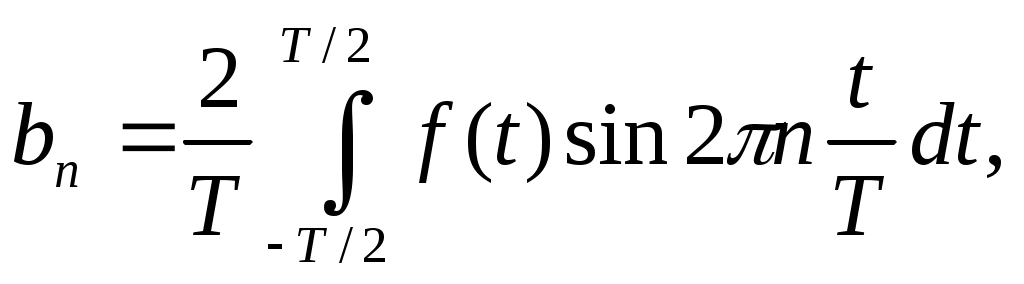
величина C0выражает среднее значение функции за период и называется постоянной составляющей, которая вычисляется по формуле:
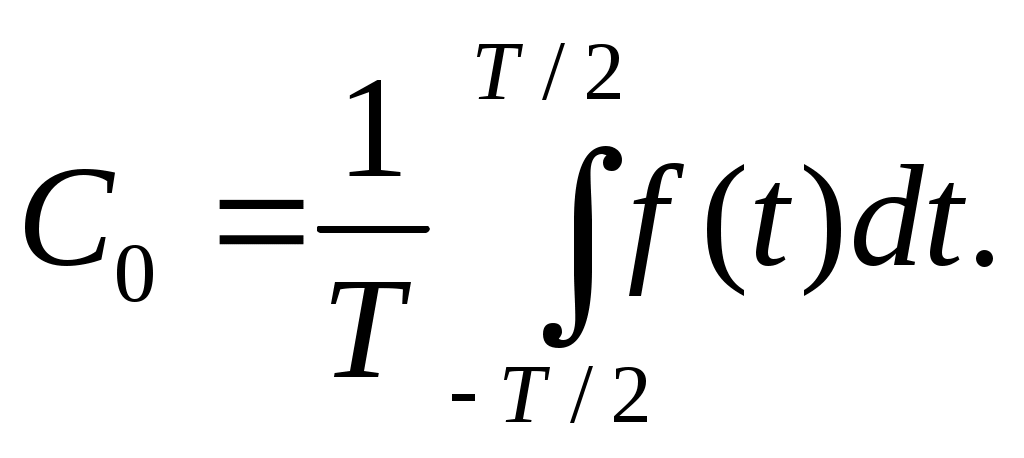
В теории колебаний и спектрального анализа представление функции f(t) в ряд Фурье записывается в виде:
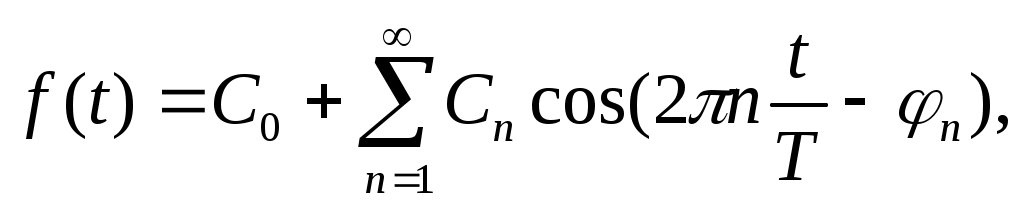 (***)
(***)
т.е. периодическая функция представлена суммой слагаемых, каждое из которых есть синусоидальное колебание с амплитудой Сn и начальной фазой n, то есть ряд Фурье периодической функции состоит из отдельных гармоник с частотами, отличающимися друг от друга на постоянное число. Причем каждая гармоника имеет определенную амплитуду. Значения Сn и n должны быть надлежащим образом подобраны для того, чтобы равенство (***) выполнялось, то есть определяются по формулам (**) [Сn = Аn].
Перепишем ряд Фурье (***) в виде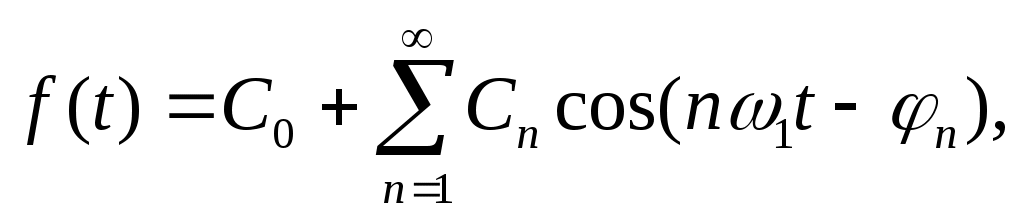 где 1
где 1
– основная частота. Отсюда можно сделать вывод: сложная периодическая функция f(t) определяется совокупностью величин Сn и n .
Определение 10. Совокупность величин Сn , то есть зависимость амплитуды от частоты, называется амплитудным спектром функции или спектром амплитуд.
Определение 11. Совокупность величин n носит название спектра фаз.
Когда говорят просто “спектр”, то подразумевают именно амплитудный спектр, в остальных случаях делают соответствующие оговорки. Периодическая функция имеет дискретный спектр (то есть она может быть представлена в виде отдельных гармоник).
Спектр периодической функции можно изобразить графически. Выберем для этого координаты Сn и = n1. Спектр будет изображен в этой системе координат совокупностью дискретных точек, т.к. каждому значению n1 соответствует одно определенное значение Сn . График, состоящий из отдельных точек, неудобен. Поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины (рис. 2).
Р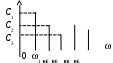
 ис. 2.
ис. 2.
Этот дискретный спектр часто называют линейчатым. Он - гармонический спектр, т.е. состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Отдельные гармоники, в том числе первая, могут отсутствовать, т.е. амплитуды их могут равняться нулю, но это не нарушает гармоничности спектра.
Дискретные, или линейчатые, спектры могут принадлежать как периодическим, так и непериодическим функциям. В первом случае спектр обязательно гармонический.
Разложение в ряд Фурье может быть обобщено на случай непериодической функции. Для этого надо применить предельный переход при Т∞, рассматривая непериодическую функцию как предельный случай периодической при неограниченно возрастающем периоде. Вместо 1/Т введем круговую основную частоту 1= 2/Т. Эта величина – есть частотный интервал между соседними гармониками, частоты которых равны 2n/Т. Если Т ∞, то 1 d и 2n/Т , где – текущая частота, изменяющаяся непрерывно, d – ее приращение. При этом ряд Фурье перейдет в интеграл Фурье, который представляет собой разложение непериодической функции в бесконечном интервале (–∞;∞) на гармонические колебания, частоты которых
непрерывно меняются от 0 до ∞:
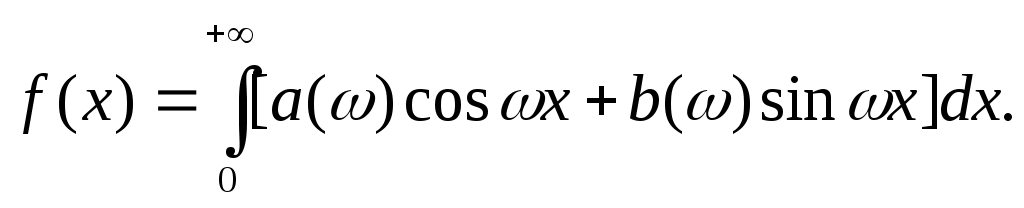
Непериодическая функция имеет непрерывный или сплошной спектры, т.е. вместо отдельных точек спектр изображается непрерывной кривой. Это получается в результате предельного перехода от ряда к интегралу Фурье: интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр изображается непрерывной последовательностью точек, т.е. непрерывной кривой. Функции a() и b() дают закон распределения амплитуд и начальных фаз в зависимости от частоты .
§ 4. Разложение в ряд Фурье четных и нечетных функций периода 2.
Определение 12. Функция f(x) называется четной, если она не меняется при изменении знака ее аргумента, т.е. если f(–х) = f(x).
График четной функции симметричен относительно оси координат.
Определение 13.Функция f(x) называется нечетной, если при изменении знака аргумента она меняет знак, но сохраняет абсолютную величину, т.е. если
f(–х) = – f(x).
График нечетной функции симметричен относительно начала координат.
Функция может не быть ни четной, ни нечетной.
Теорема 5. Произведение двух функций одинаковой (различной) четности четно (нечетно). Сумма четных функций – четная функция, нечетных функций – нечетная.
Лемма. Верна формула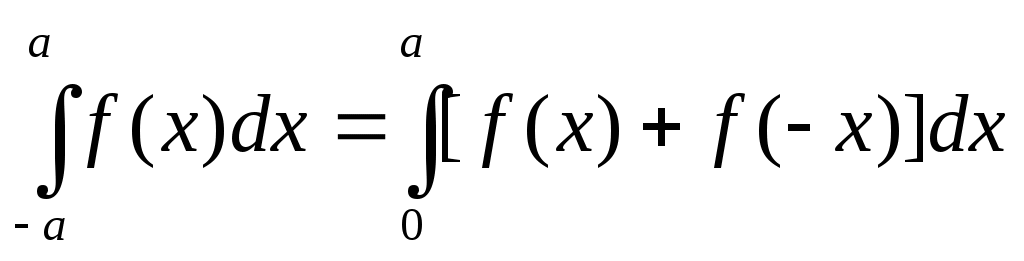 .
.
Теорема 6. Если f(x) четна, то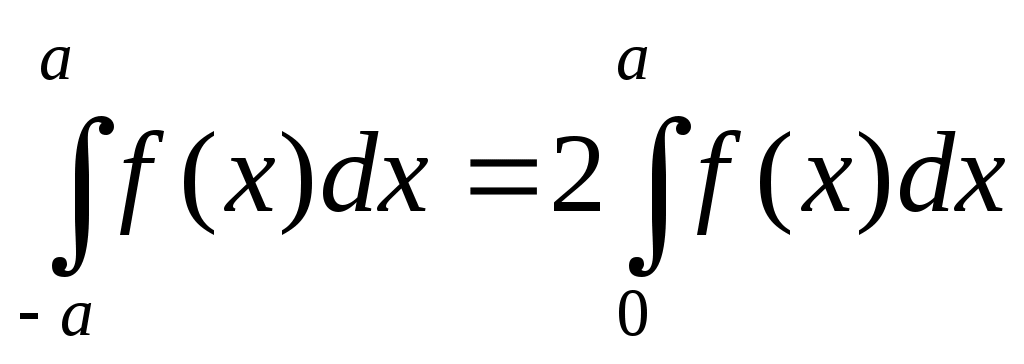 . (1.15)
. (1.15)
Если же f(x) нечетна, то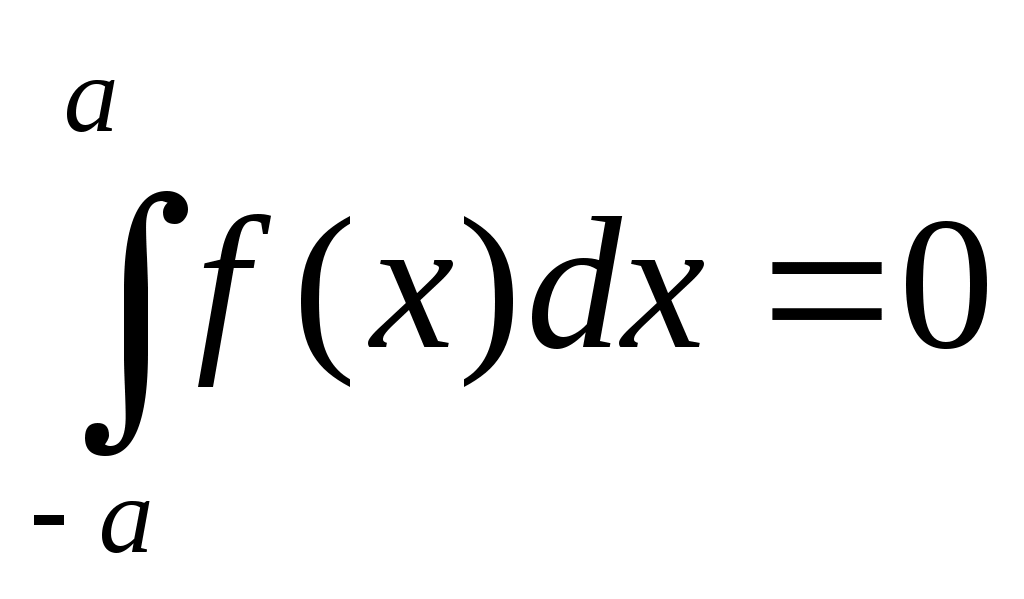 . (1.16)
. (1.16)
Пусть f(x) – четная функция, тогда ее коэффициент Фурье а0 по формуле (1.15) может быть записан в виде
а0 =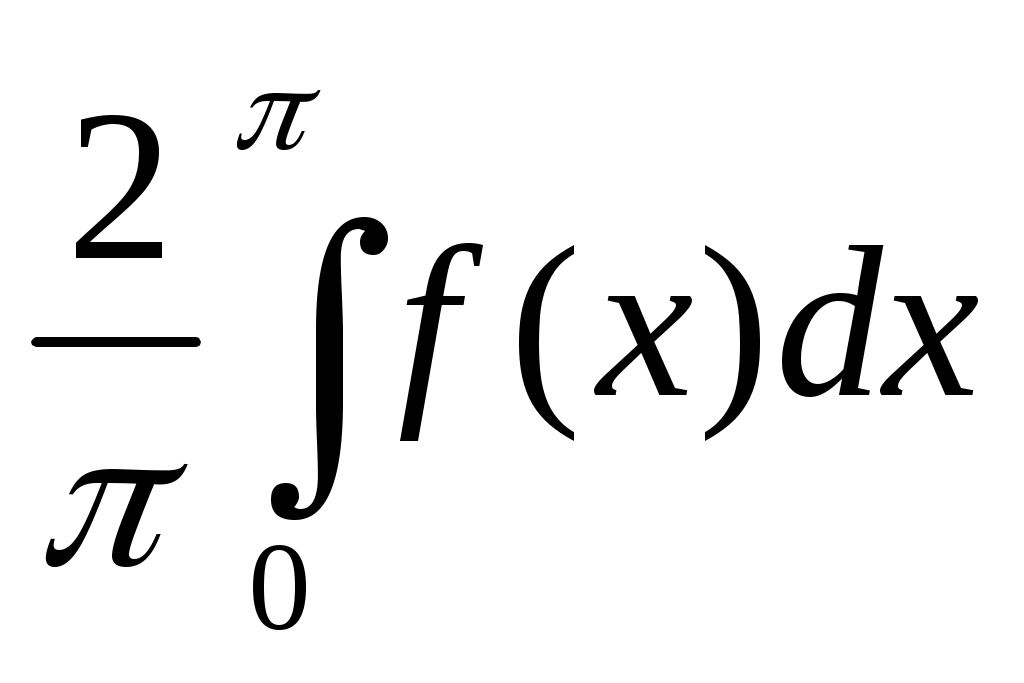 . (1.17)
. (1.17)
Поскольку произведение f(x) cos nx четно по теореме 5, то по той же формуле (1.15)
аn =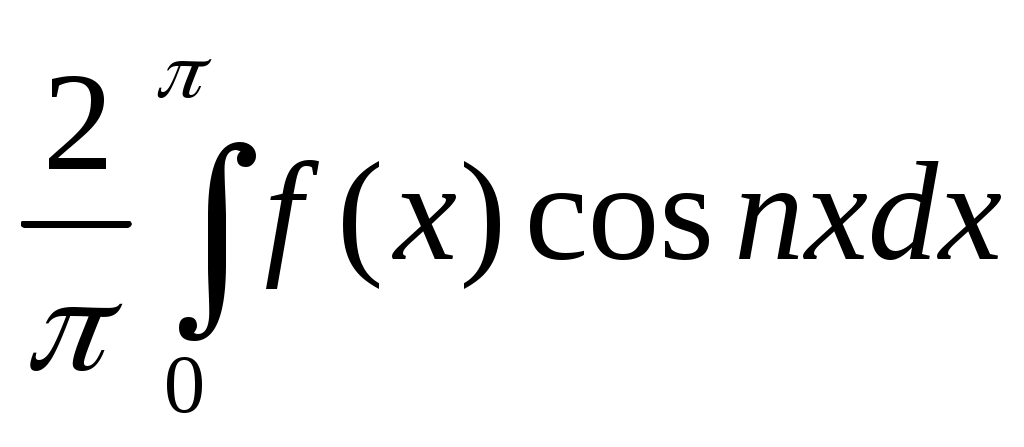 . (1.18)
. (1.18)
bn = 0, так как произведение f(x) sin nx нечетно по теореме 5 и к bn применима формула (1.16). Отсюда следует
Теорема 7. Ряд Фурье четной функции f(x) не содержит членов с синусами и имеет вид:
f(x) = +
+ 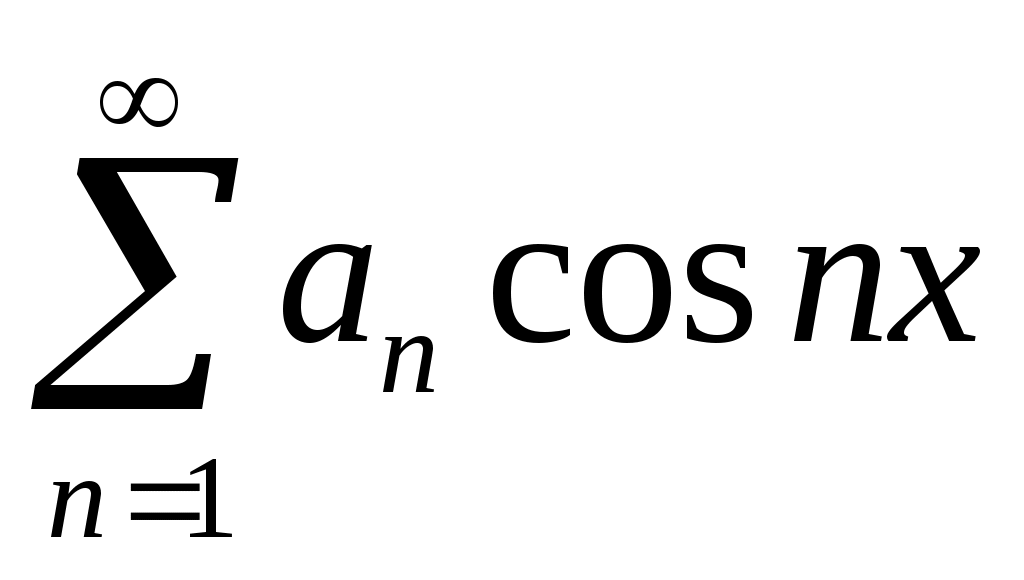 , (1.19)
, (1.19)
причем его коэффициенты можно находить по упрощенным формулам (1.17), (1.18).
Таким же способом устанавливается
Теорема 8. Ряд Фурье нечетной функции f(x) не содержит ни свободного члена, ни членов с косинусами и имеет вид:
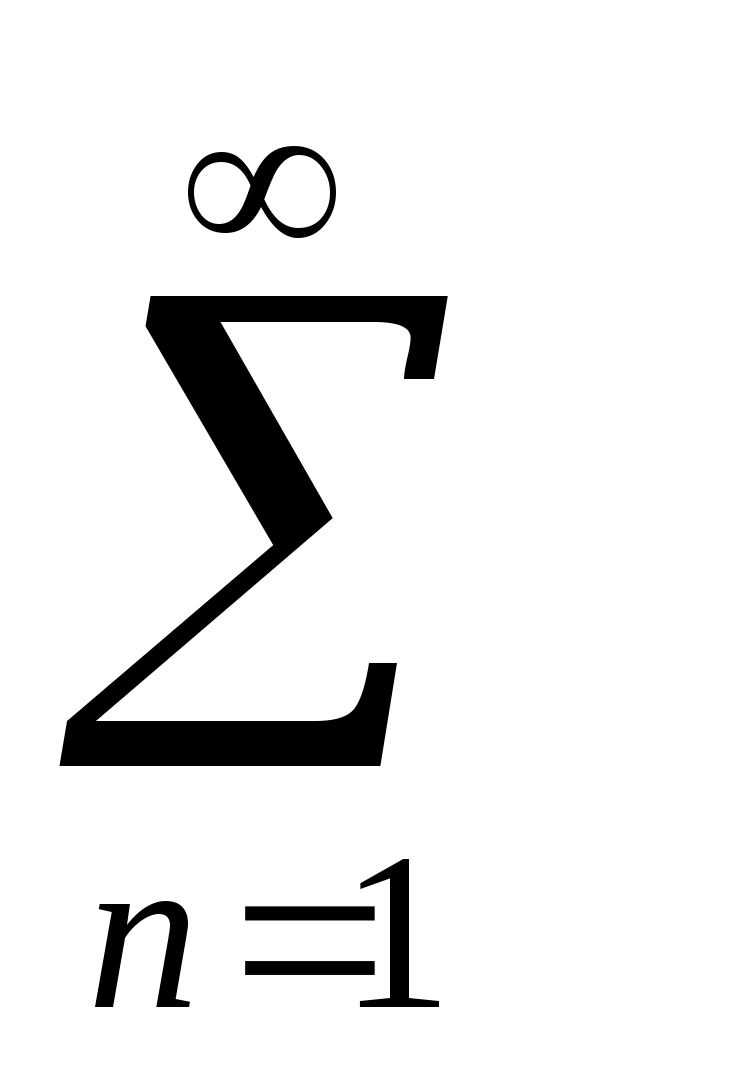
bn =
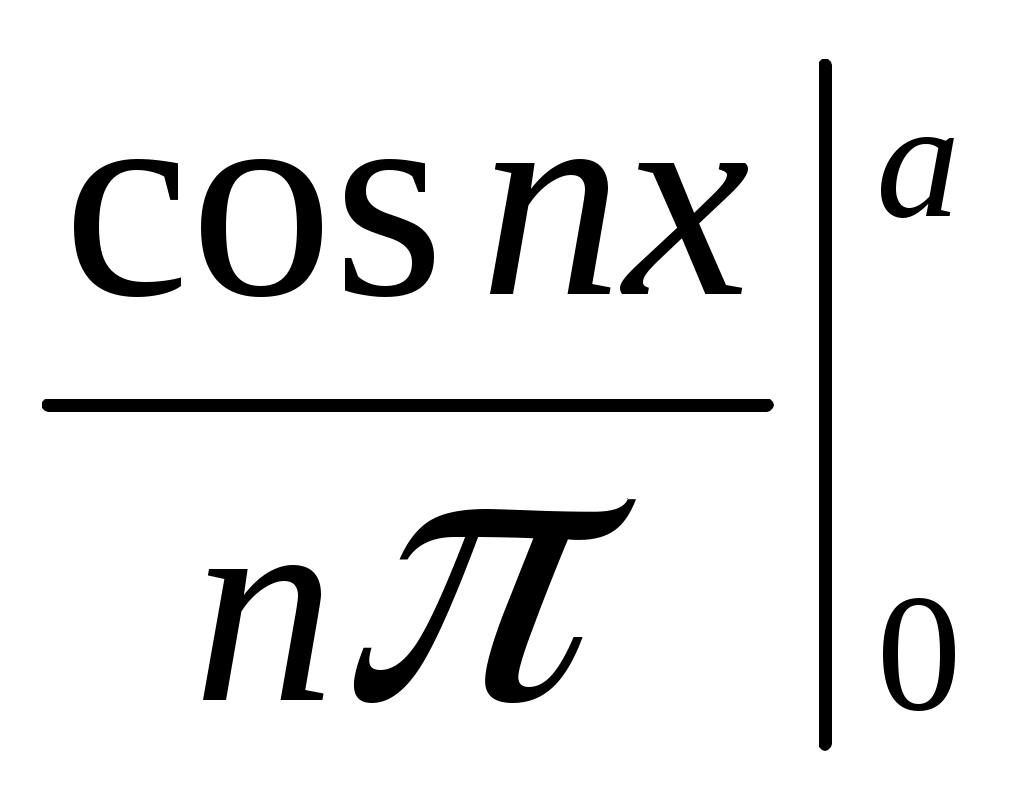 = –
= –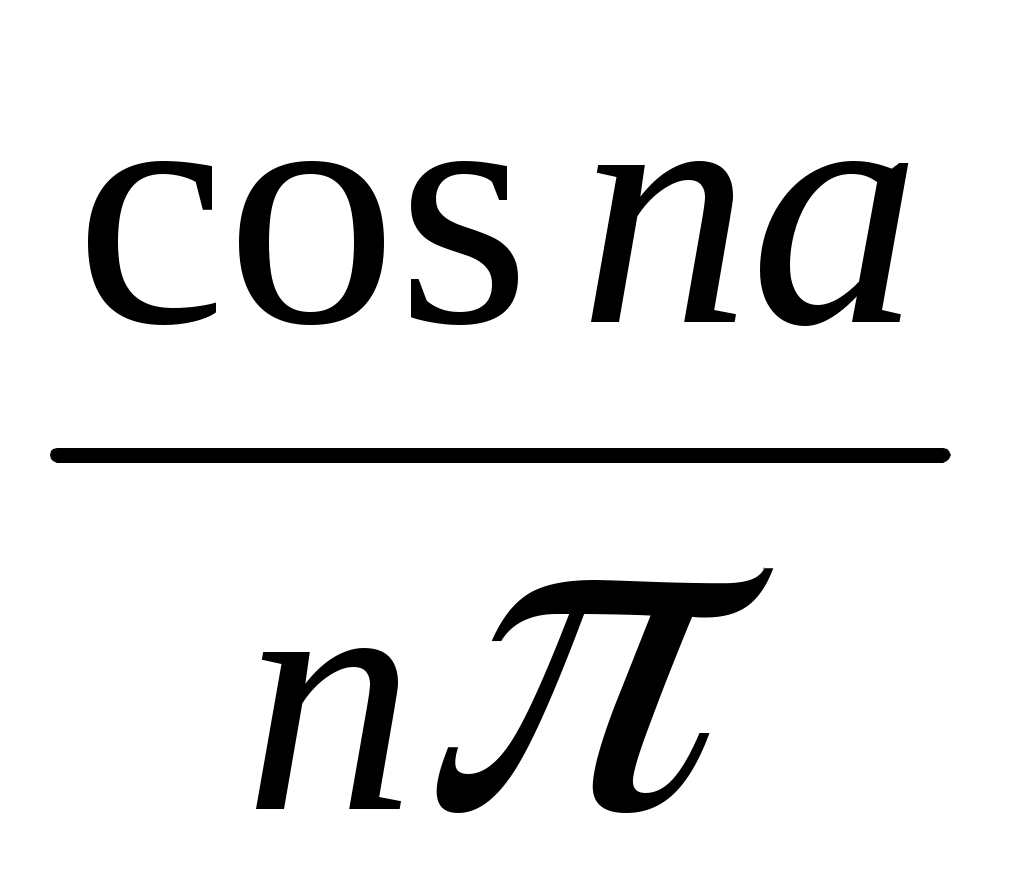 +
+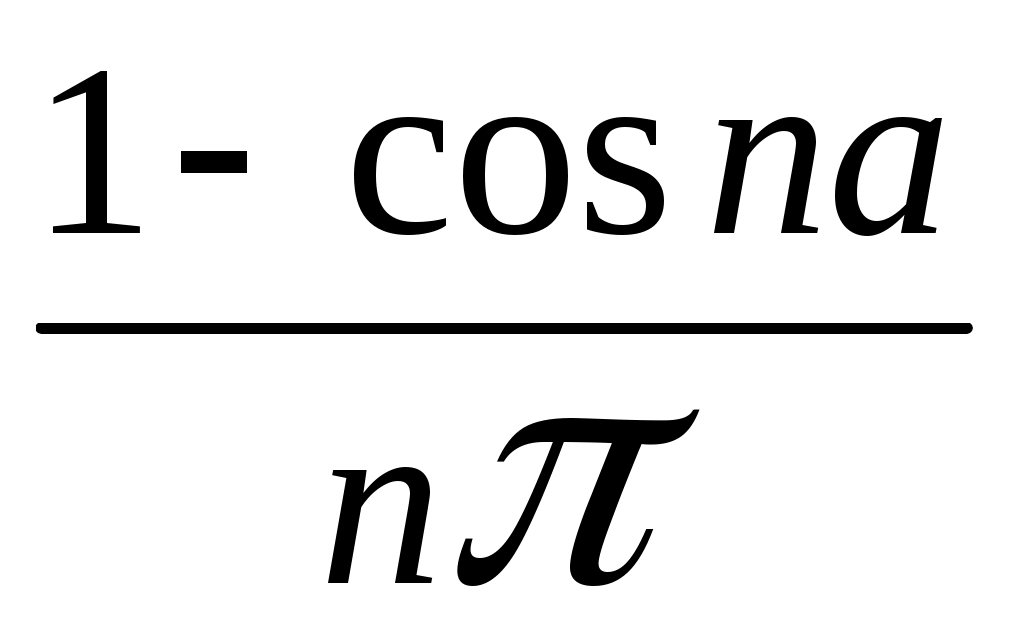 , при n 0.
, при n 0.Следовательно,
f(x) =
В интервале [-; ] ряд сходится к функции f(x), в точках х = к 0: ( 1/2 [ f(–+0) + f(–0)] = 0 ), в точках х = a, x= 0 к 1/2 : ( 1/2 [ f(х-0) + f(х+0)] = =1/2 ).
Ряд Фурье в виде простых гармоник. Спектры.
Практически любую периодическую функцию можно разложить на простые гармоники с помощью тригонометрического ряда (ряда Фурье):
f(x) =
Запишем данный ряд в виде суммы простых гармоник, полагая коэффициенты равными an= Ansinn, bn= Ancosn . Получим: ancos n + bnsinn = Ansin( nx+ n ), где
An =
Тогда ряд (*) в виде простых гармоник примет вид
f(x) =
Ряд Фурье представляет периодическую функцию суммой хотя и бесконечного числа синусоид, но с частотами, имеющими определенное дискретное значение.
Иногда n-ую гармонику записывают в виде ancos nx + bnsin nx = Ancos(nx – n) , где an= Ancosn , bn= An sinn .
При этом An и n определяются по формулам (**). Тогда ряд (*) примет вид
f(x) =
Определение 9. Операция представления периодической функции f(x) рядом Фурье называется гармоническим анализом.
Выражение (*) встречается и в другой, более употребительной форме:
Коэффициенты an, bn определяются по формулам:
величина C0выражает среднее значение функции за период и называется постоянной составляющей, которая вычисляется по формуле:
В теории колебаний и спектрального анализа представление функции f(t) в ряд Фурье записывается в виде:
т.е. периодическая функция представлена суммой слагаемых, каждое из которых есть синусоидальное колебание с амплитудой Сn и начальной фазой n, то есть ряд Фурье периодической функции состоит из отдельных гармоник с частотами, отличающимися друг от друга на постоянное число. Причем каждая гармоника имеет определенную амплитуду. Значения Сn и n должны быть надлежащим образом подобраны для того, чтобы равенство (***) выполнялось, то есть определяются по формулам (**) [Сn = Аn].
Перепишем ряд Фурье (***) в виде
– основная частота. Отсюда можно сделать вывод: сложная периодическая функция f(t) определяется совокупностью величин Сn и n .
Определение 10. Совокупность величин Сn , то есть зависимость амплитуды от частоты, называется амплитудным спектром функции или спектром амплитуд.
Определение 11. Совокупность величин n носит название спектра фаз.
Когда говорят просто “спектр”, то подразумевают именно амплитудный спектр, в остальных случаях делают соответствующие оговорки. Периодическая функция имеет дискретный спектр (то есть она может быть представлена в виде отдельных гармоник).
Спектр периодической функции можно изобразить графически. Выберем для этого координаты Сn и = n1. Спектр будет изображен в этой системе координат совокупностью дискретных точек, т.к. каждому значению n1 соответствует одно определенное значение Сn . График, состоящий из отдельных точек, неудобен. Поэтому принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины (рис. 2).
Р
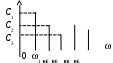
 ис. 2.
ис. 2.Этот дискретный спектр часто называют линейчатым. Он - гармонический спектр, т.е. состоит из равноотстоящих спектральных линий; частоты гармоник находятся в простых кратных соотношениях. Отдельные гармоники, в том числе первая, могут отсутствовать, т.е. амплитуды их могут равняться нулю, но это не нарушает гармоничности спектра.
Дискретные, или линейчатые, спектры могут принадлежать как периодическим, так и непериодическим функциям. В первом случае спектр обязательно гармонический.
Разложение в ряд Фурье может быть обобщено на случай непериодической функции. Для этого надо применить предельный переход при Т∞, рассматривая непериодическую функцию как предельный случай периодической при неограниченно возрастающем периоде. Вместо 1/Т введем круговую основную частоту 1= 2/Т. Эта величина – есть частотный интервал между соседними гармониками, частоты которых равны 2n/Т. Если Т ∞, то 1 d и 2n/Т , где – текущая частота, изменяющаяся непрерывно, d – ее приращение. При этом ряд Фурье перейдет в интеграл Фурье, который представляет собой разложение непериодической функции в бесконечном интервале (–∞;∞) на гармонические колебания, частоты которых
непрерывно меняются от 0 до ∞:
Непериодическая функция имеет непрерывный или сплошной спектры, т.е. вместо отдельных точек спектр изображается непрерывной кривой. Это получается в результате предельного перехода от ряда к интегралу Фурье: интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр изображается непрерывной последовательностью точек, т.е. непрерывной кривой. Функции a() и b() дают закон распределения амплитуд и начальных фаз в зависимости от частоты .
§ 4. Разложение в ряд Фурье четных и нечетных функций периода 2.
Определение 12. Функция f(x) называется четной, если она не меняется при изменении знака ее аргумента, т.е. если f(–х) = f(x).
График четной функции симметричен относительно оси координат.
Определение 13.Функция f(x) называется нечетной, если при изменении знака аргумента она меняет знак, но сохраняет абсолютную величину, т.е. если
f(–х) = – f(x).
График нечетной функции симметричен относительно начала координат.
Функция может не быть ни четной, ни нечетной.
Теорема 5. Произведение двух функций одинаковой (различной) четности четно (нечетно). Сумма четных функций – четная функция, нечетных функций – нечетная.
Лемма. Верна формула
Теорема 6. Если f(x) четна, то
Если же f(x) нечетна, то
Пусть f(x) – четная функция, тогда ее коэффициент Фурье а0 по формуле (1.15) может быть записан в виде
а0 =
Поскольку произведение f(x) cos nx четно по теореме 5, то по той же формуле (1.15)
аn =
bn = 0, так как произведение f(x) sin nx нечетно по теореме 5 и к bn применима формула (1.16). Отсюда следует
Теорема 7. Ряд Фурье четной функции f(x) не содержит членов с синусами и имеет вид:
f(x) =
причем его коэффициенты можно находить по упрощенным формулам (1.17), (1.18).
Таким же способом устанавливается
Теорема 8. Ряд Фурье нечетной функции f(x) не содержит ни свободного члена, ни членов с косинусами и имеет вид: