ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
bn sin nx , (1.20)
гдеbn=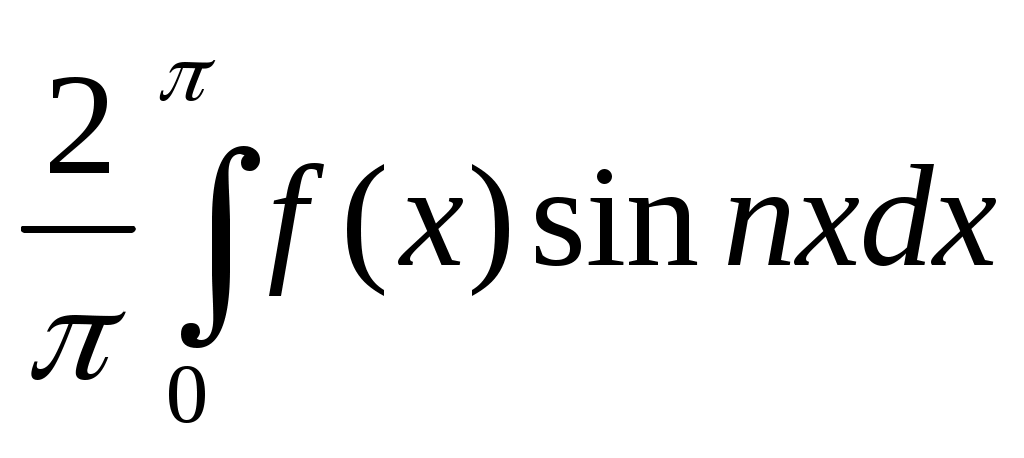 (1.21)
(1.21)
Пример 2. Разложить в ряд Фурье функцию, определенную равенством f(x) = x при – < x .
Решение:
f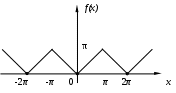 (x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.)
(x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.)
По формулам (1.17) и (1.18) найдем коэффициенты Фурье:
а0 =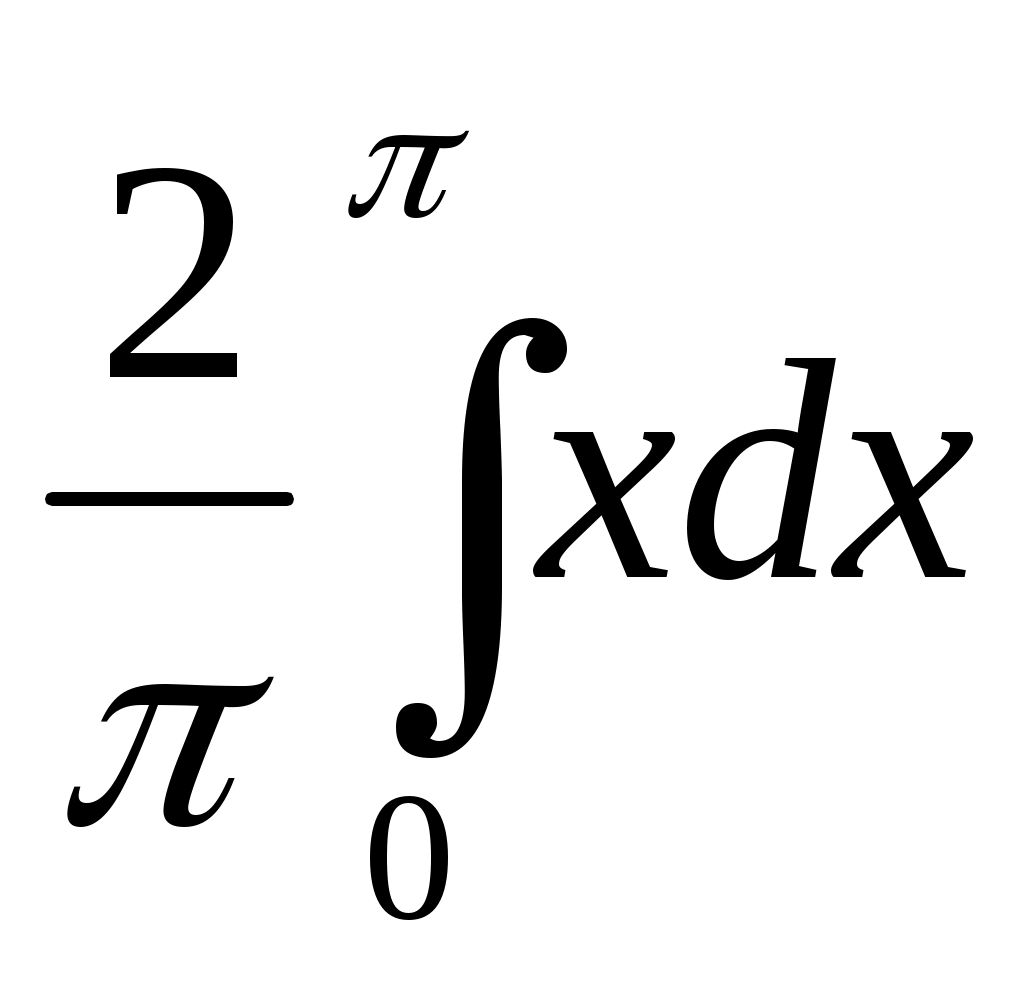 =
= 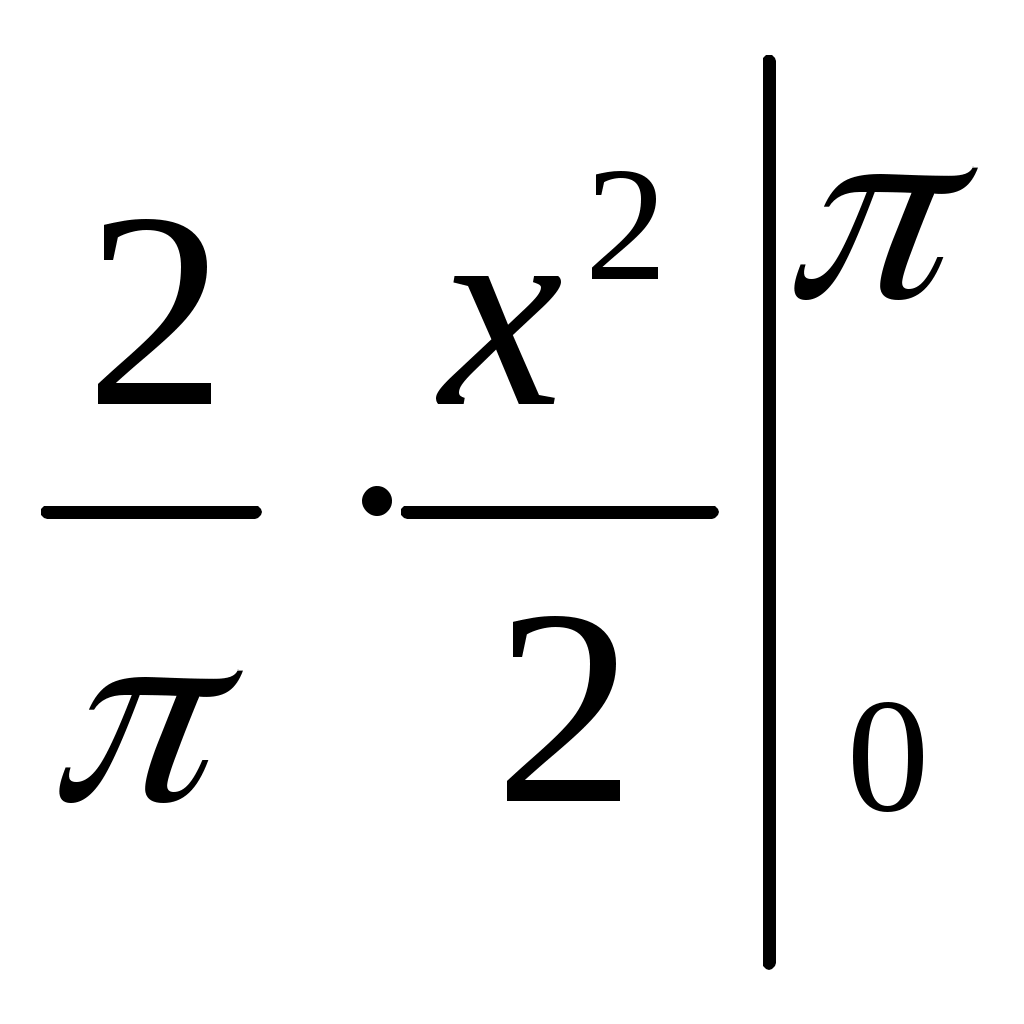 = ,
= ,
аn =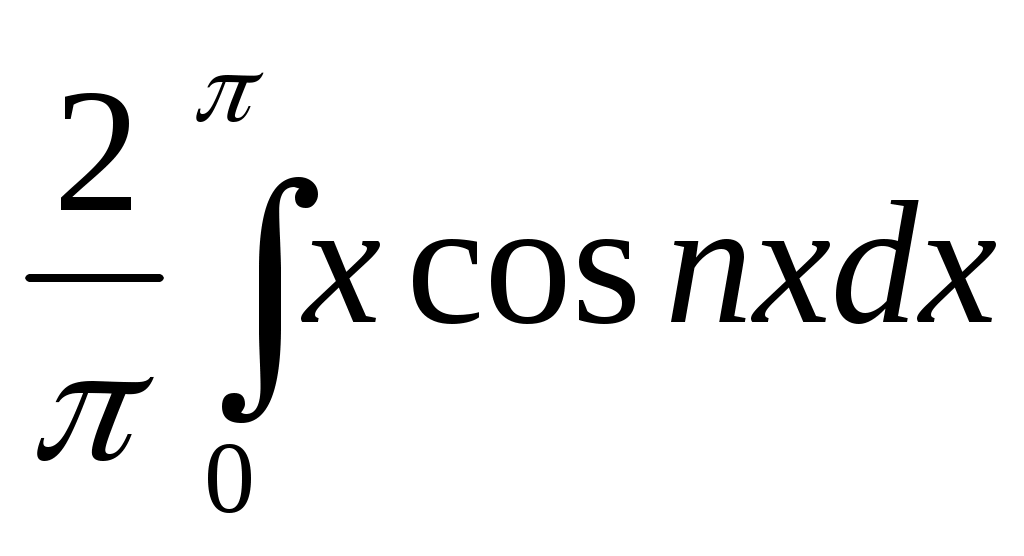 =
=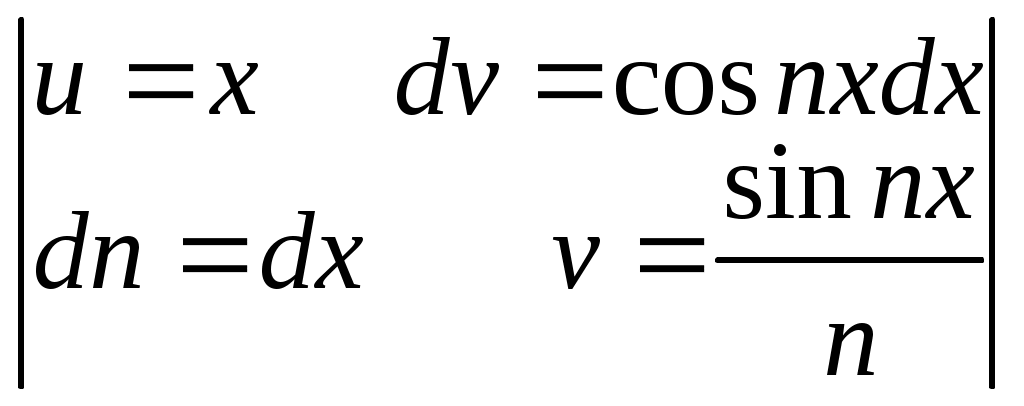 =
=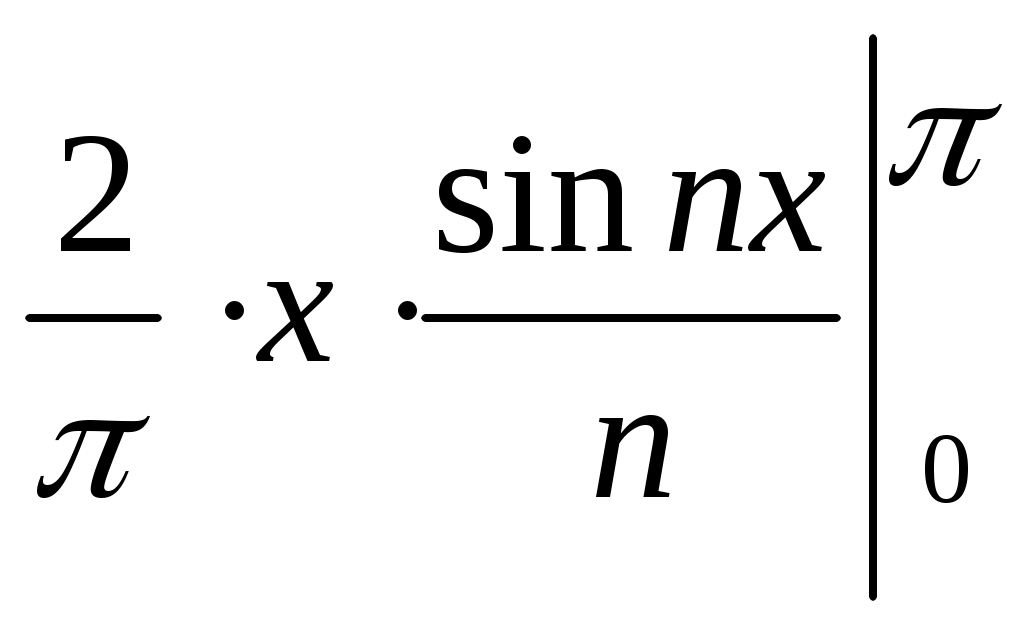 -
- 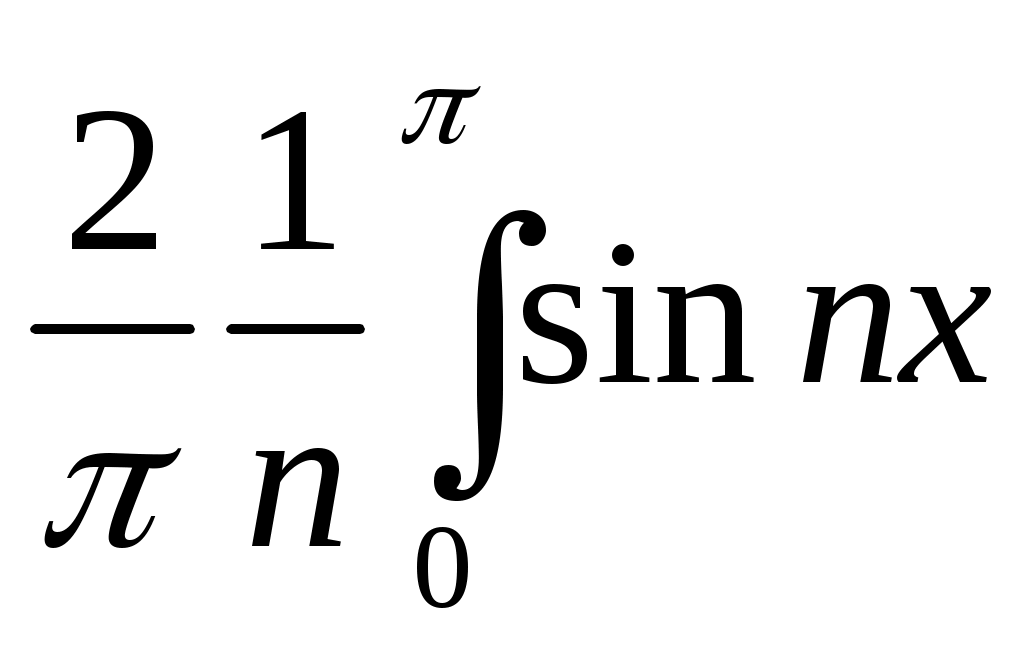 dx =
dx =
=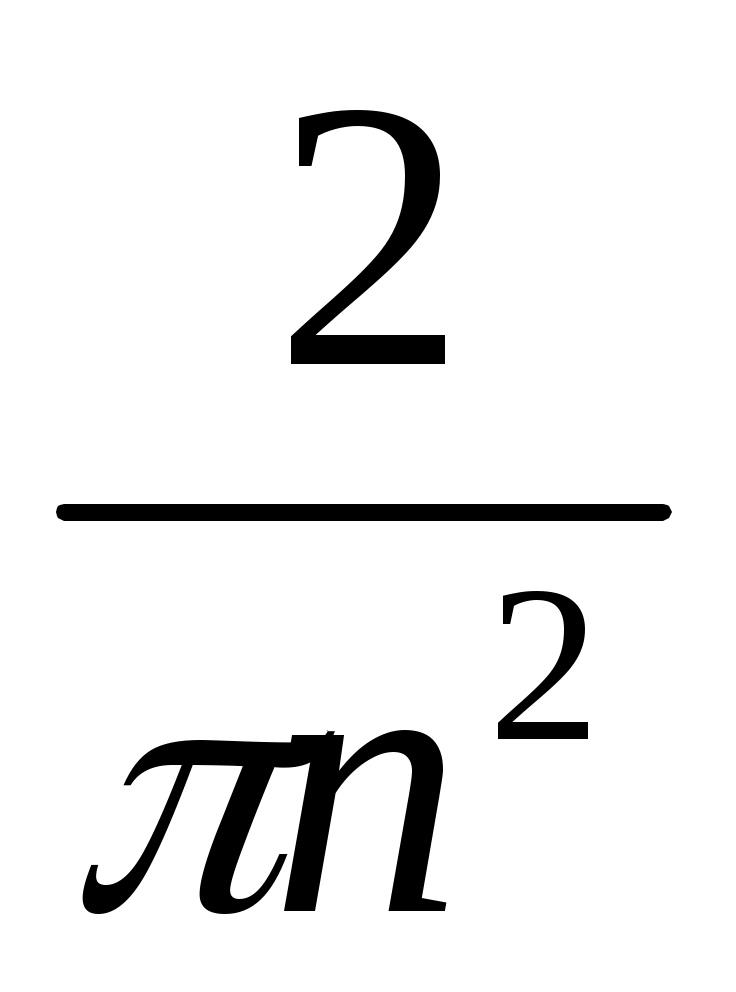 cos nx
cos nx =
= 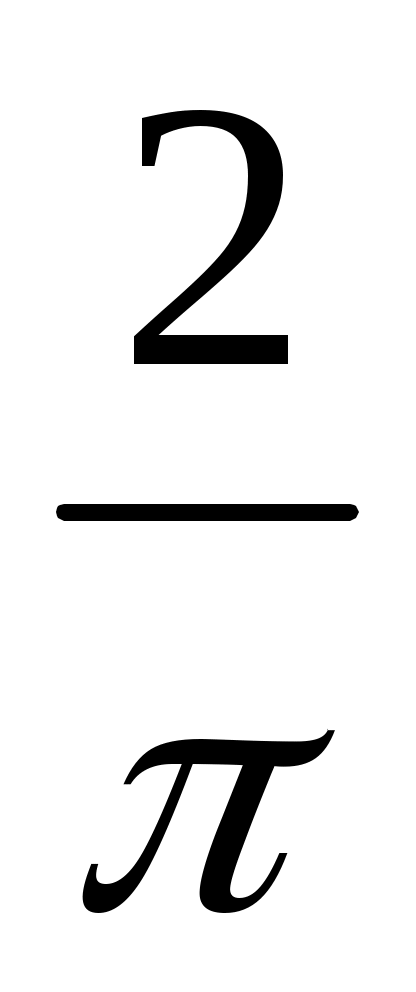
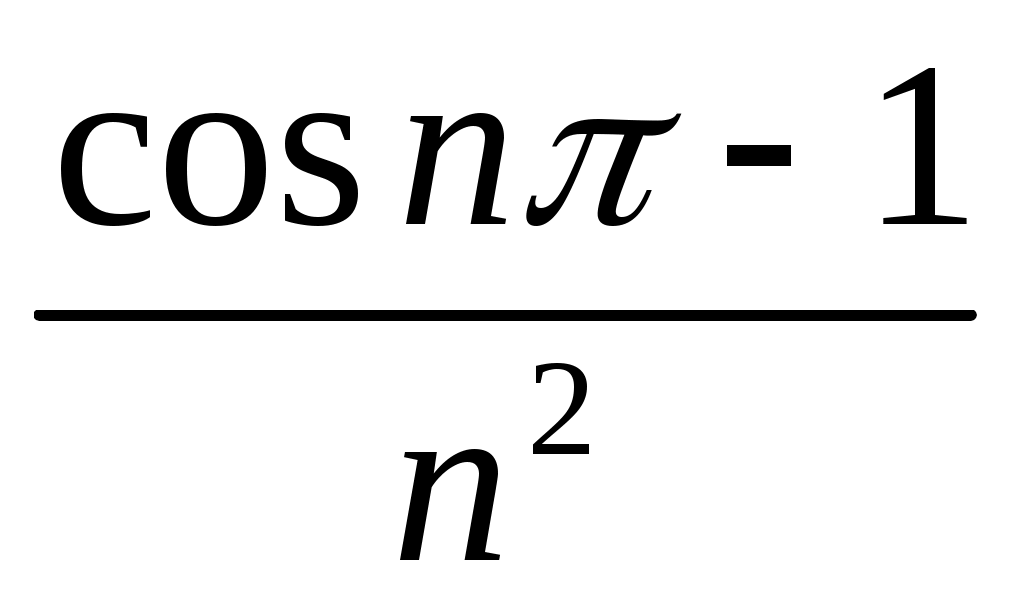 =
= 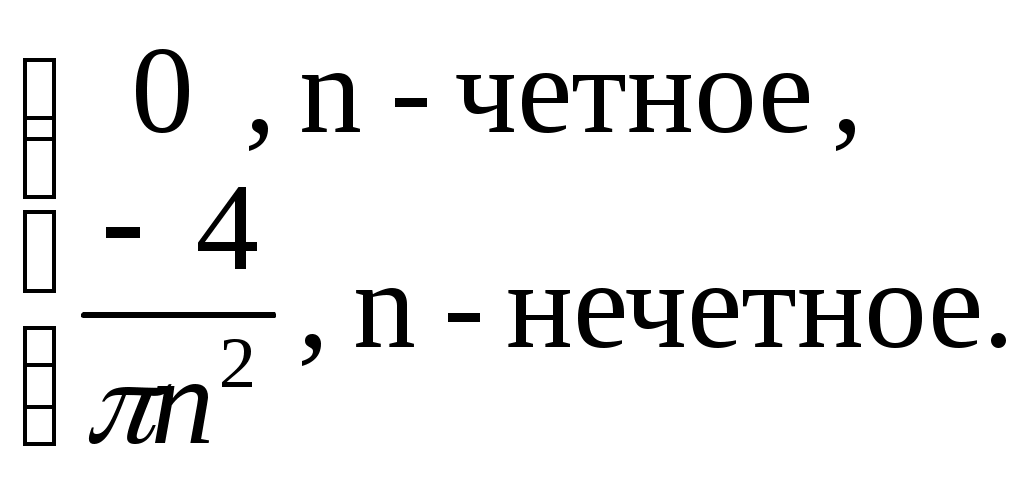
Следовательно, ряд Фурье для данной функции имеет вид:
f(x) =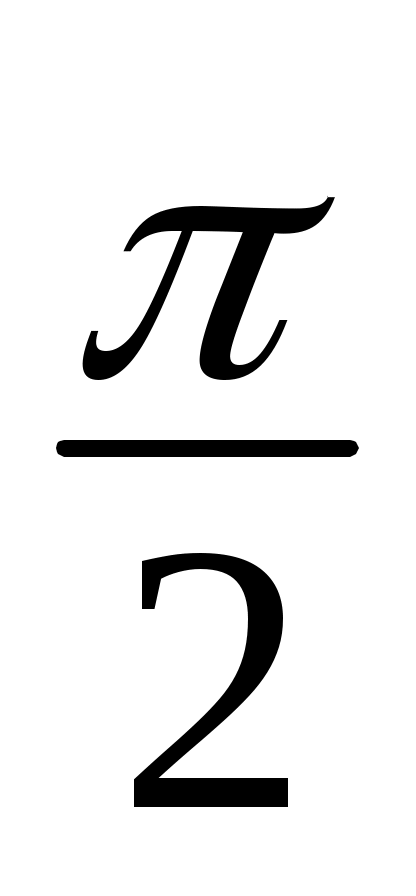 –
–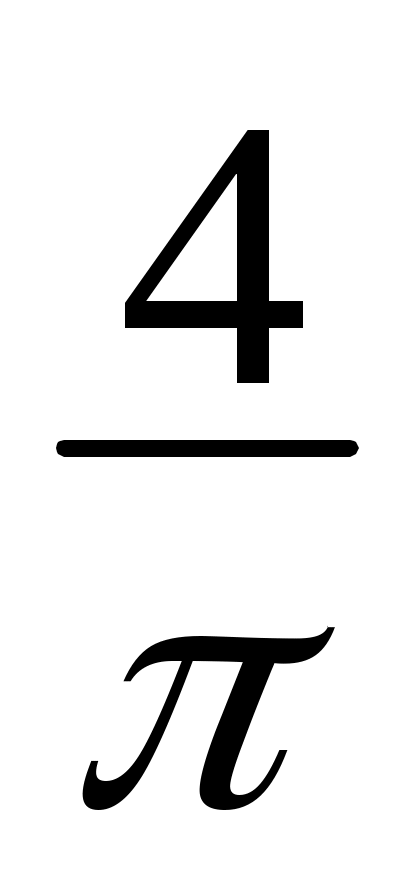 (cos x +
(cos x +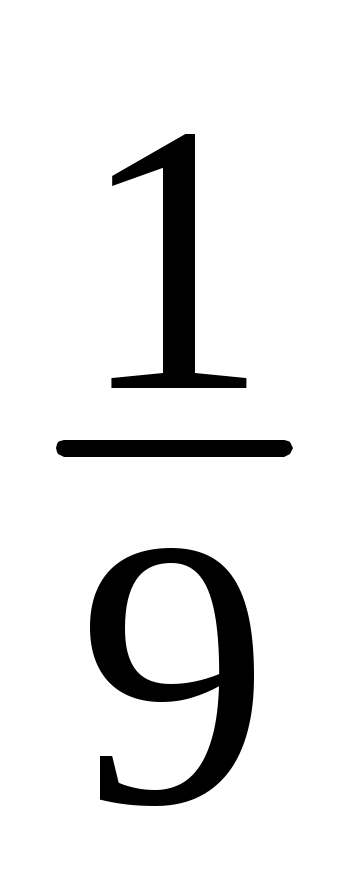 cos3x+
cos3x+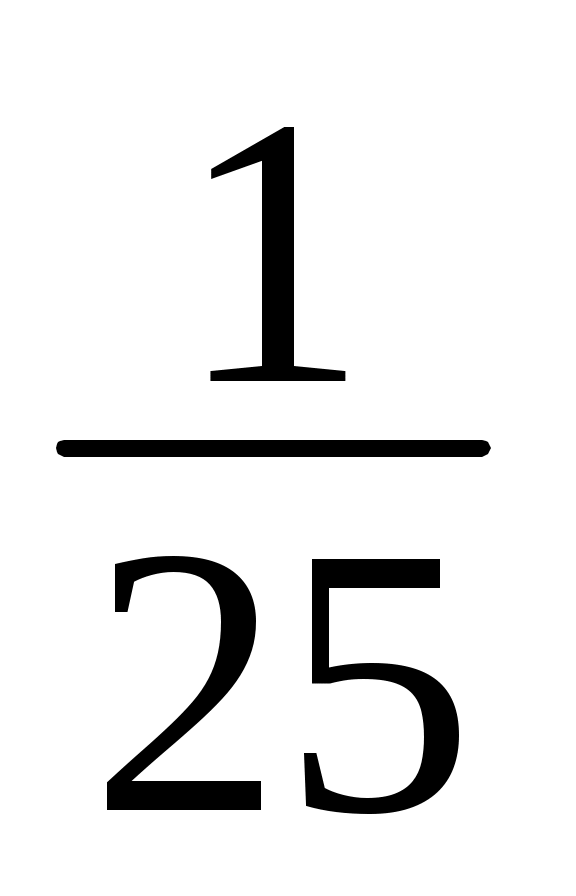 cos5x + ... +
cos5x + ... + 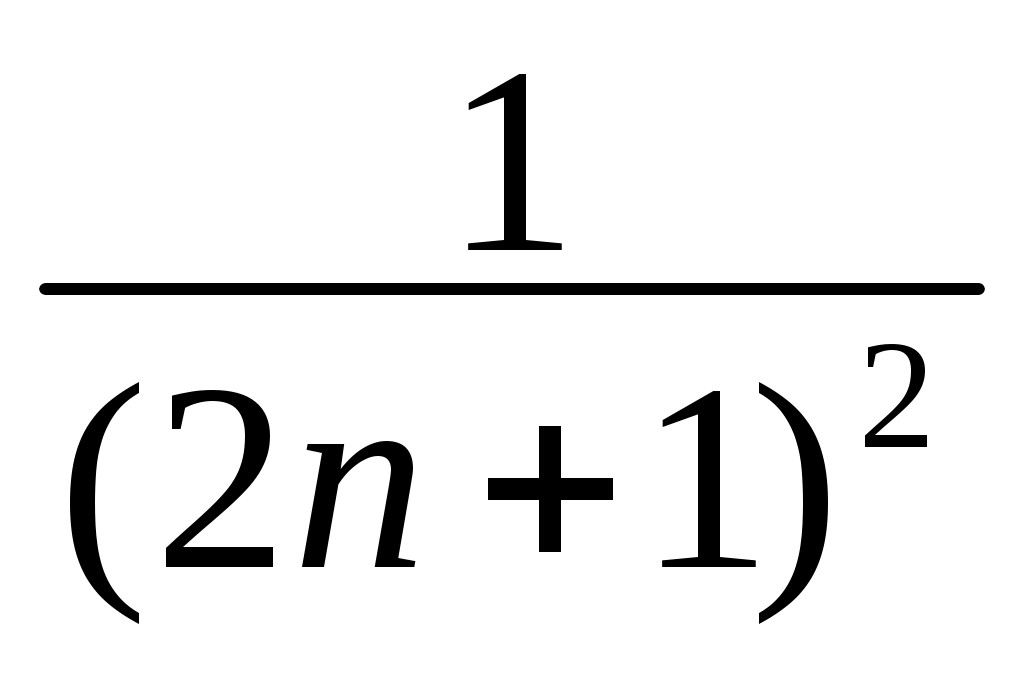 cos((2n+1)x) +...) =
cos((2n+1)x) +...) = 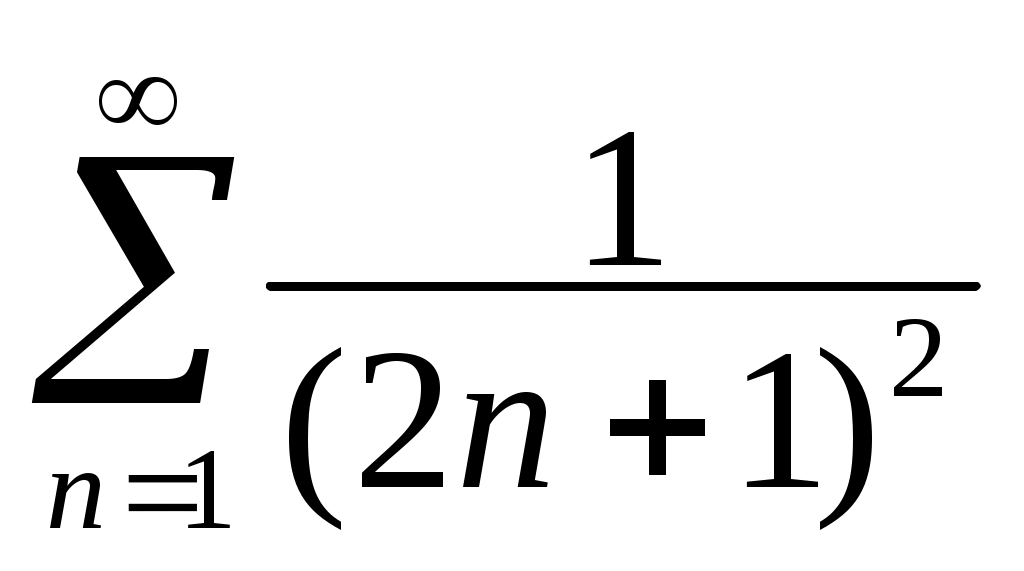 cos((2n+1)x).
cos((2n+1)x).
На интервале [–; ] ряд сходится к функции x .
Пример 3. Разложить в ряд Фурье функцию: f(x)=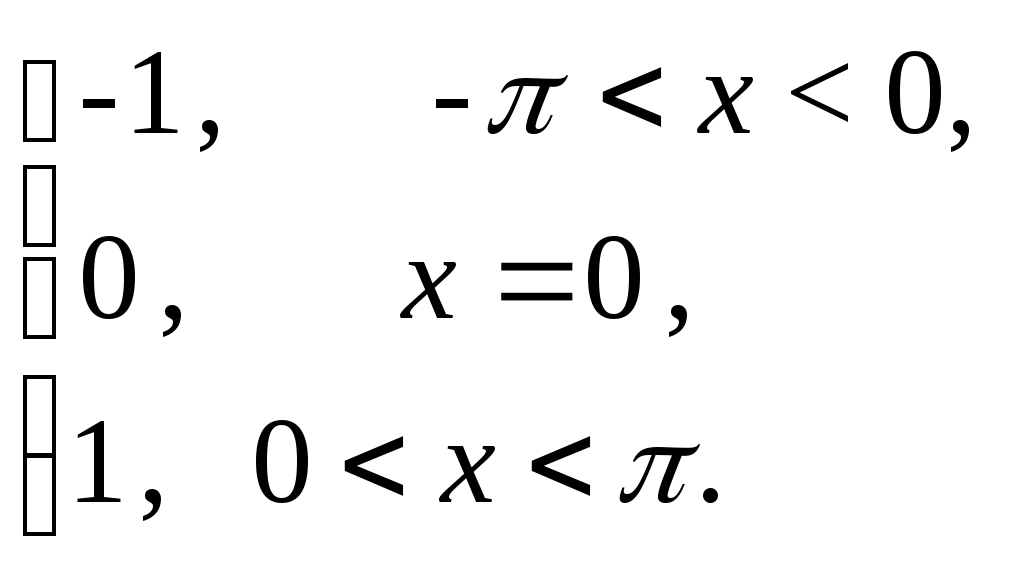
Решение:
f(x) имеет период 2. Она удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье.
f(–х) = – f(x) (см. рис. 4), т.е. f(x) – нечетна, следовательно а0 = 0 и аn= 0.
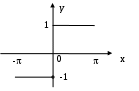
Рис. 4.
По формуле (1.21) найдем коэффициент Фурье:
b n =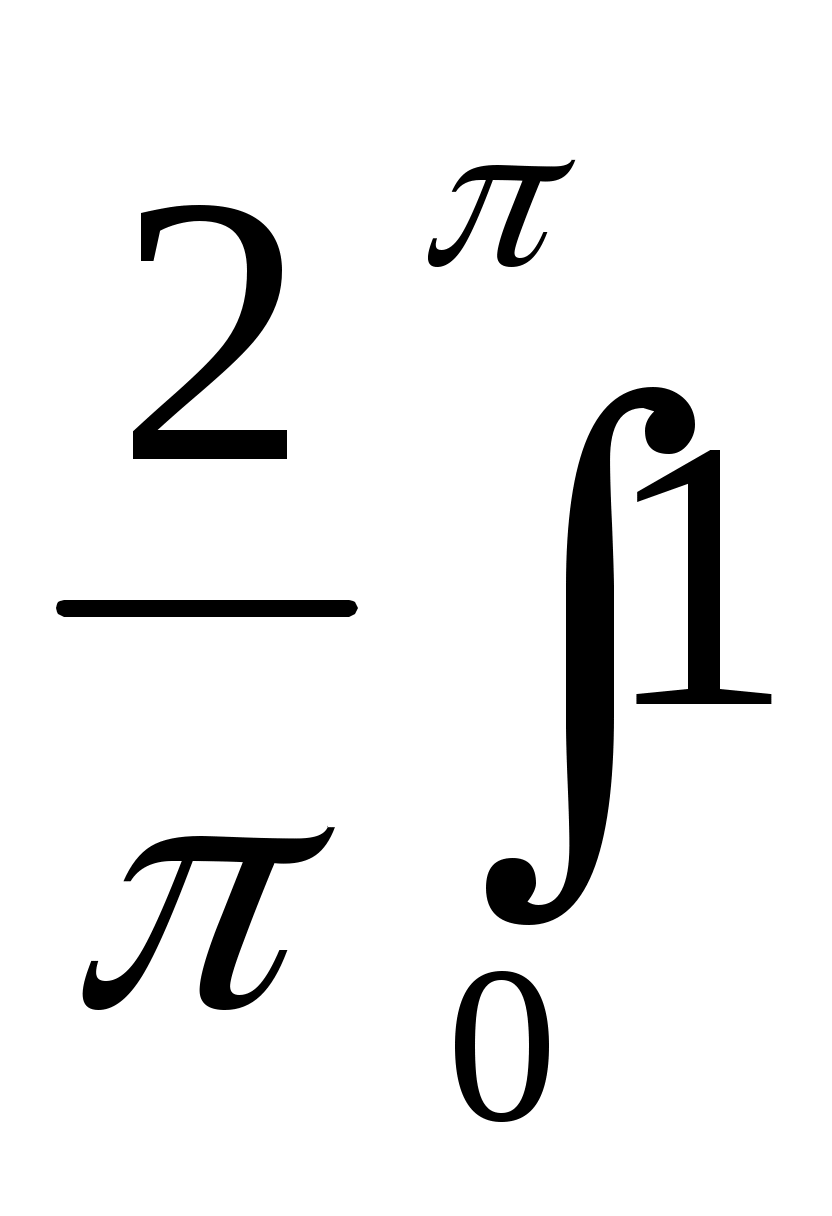 sin nx dx = -
sin nx dx = -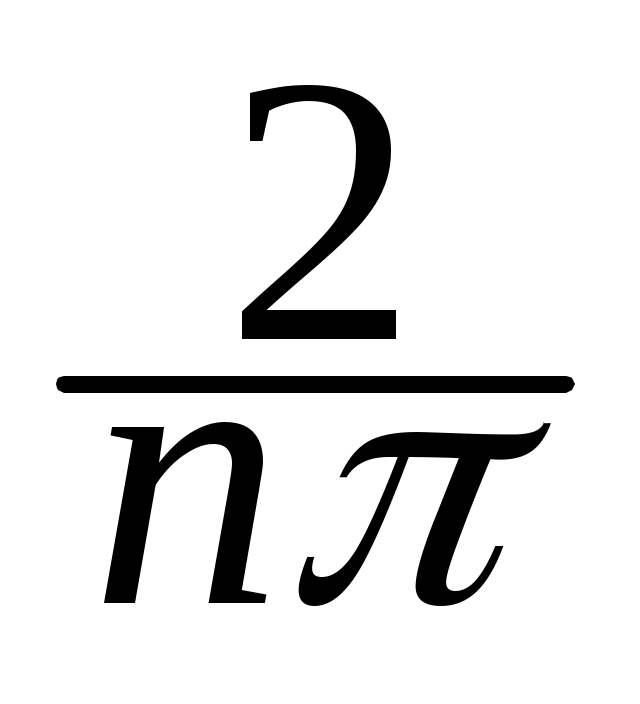 cos nx
cos nx  =
= 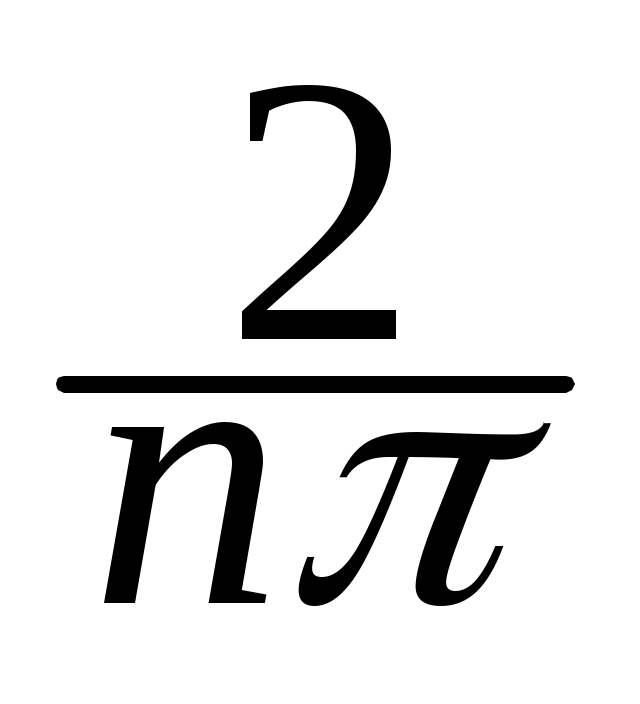 ( 1–(–1)n ) =
( 1–(–1)n ) = 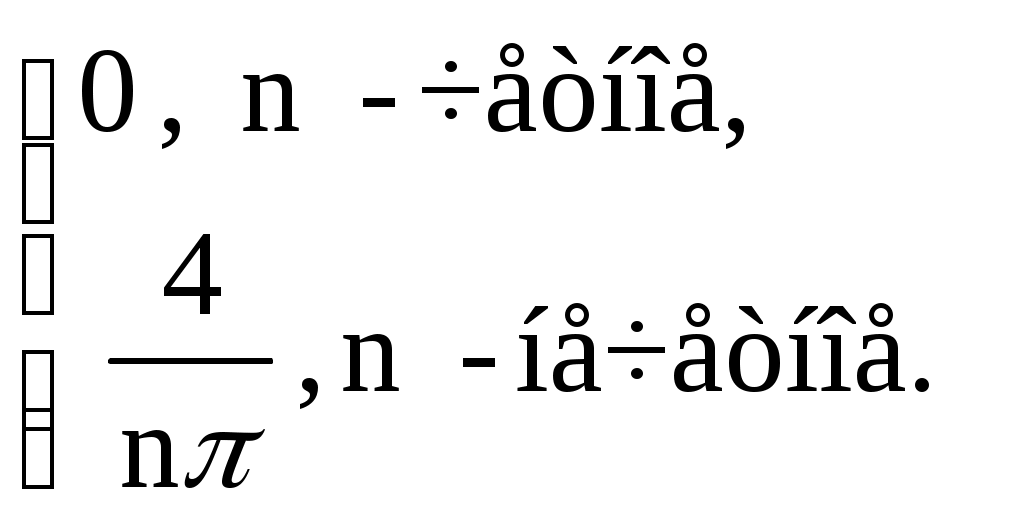
b2k+1 =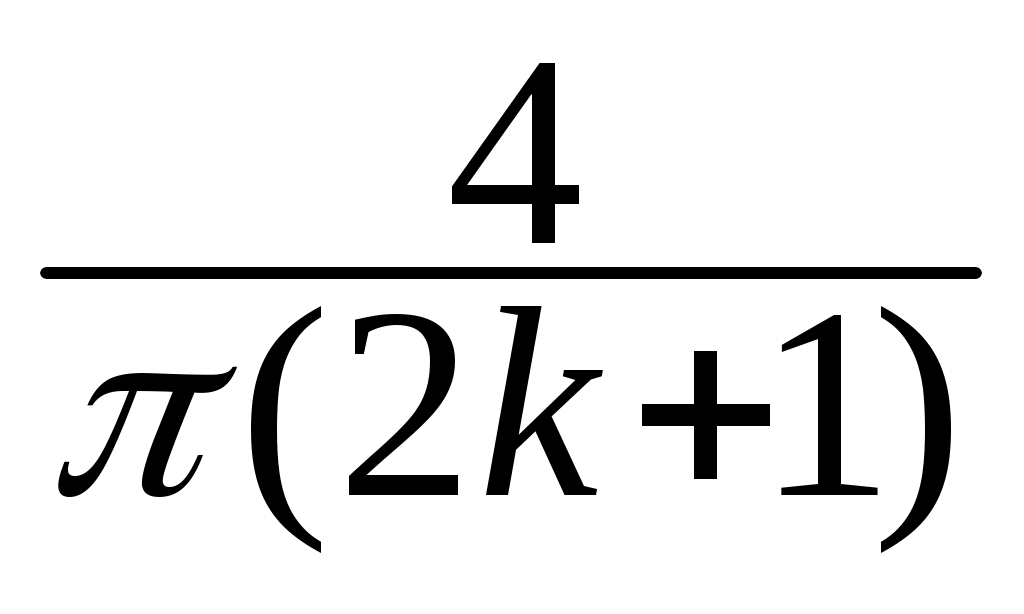 .
.
Следовательно, ряд Фурье для данной функции имеет вид:
f(x) =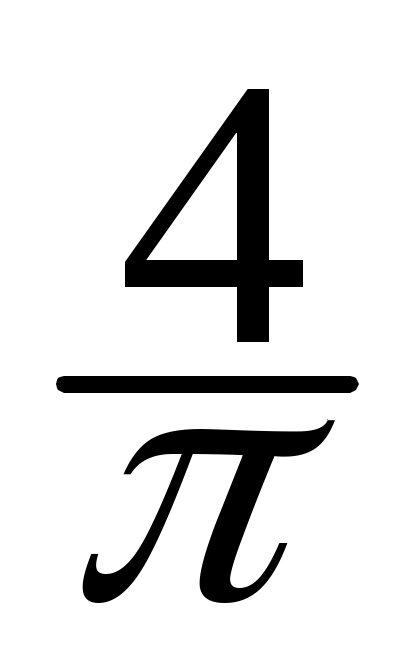 (sin x +
(sin x + 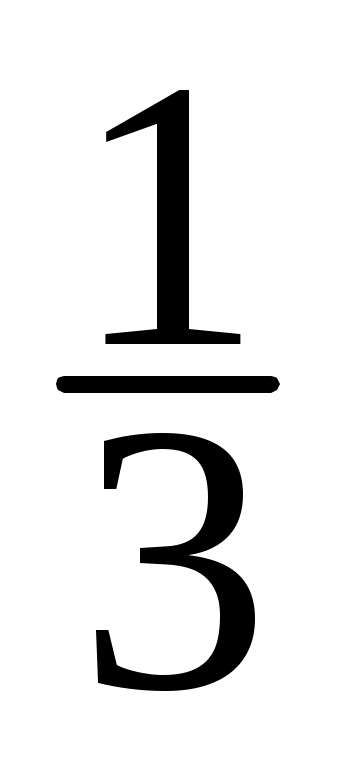 sin x +
sin x + 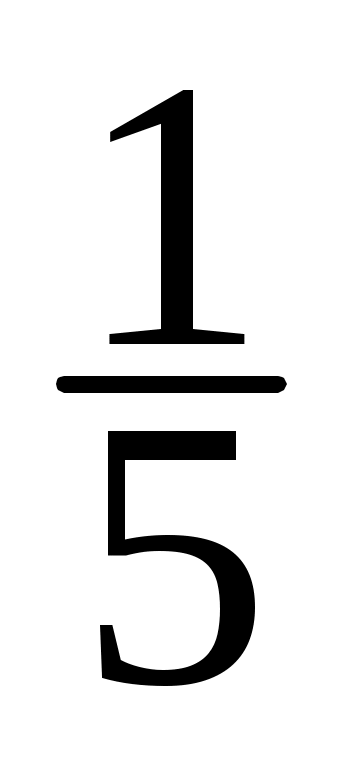 sin x + ... +
sin x + ... + 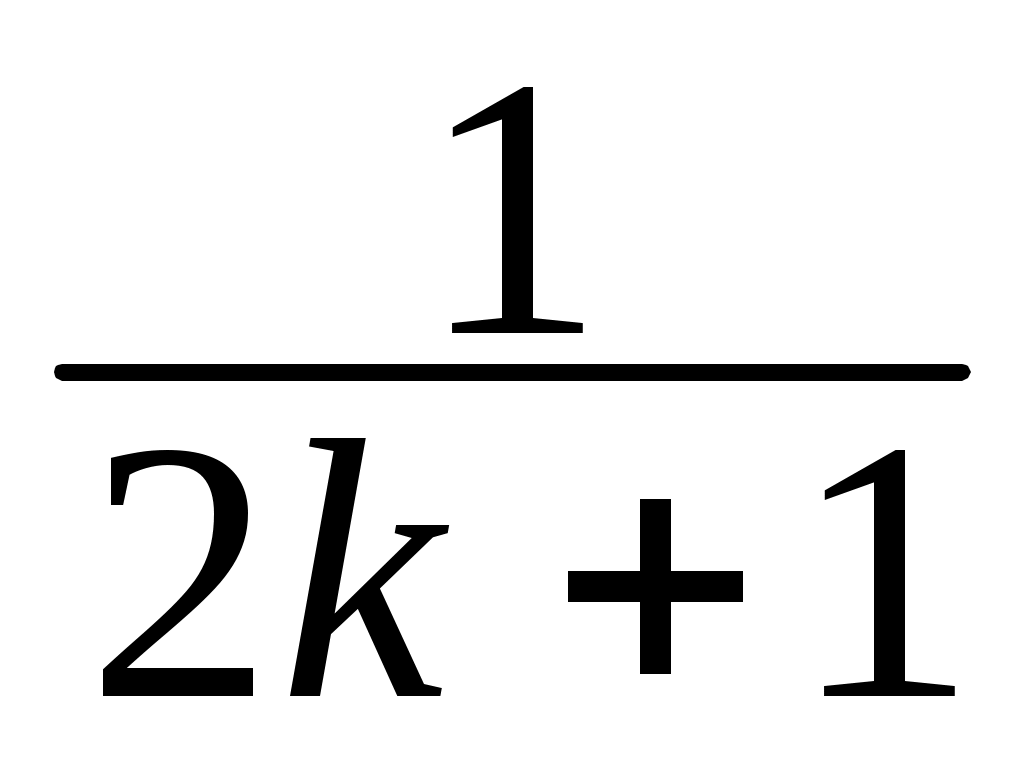 sin((2k+1)·x ) ), ( k = 0,1,2,... )
sin((2k+1)·x ) ), ( k = 0,1,2,... )
f(x) =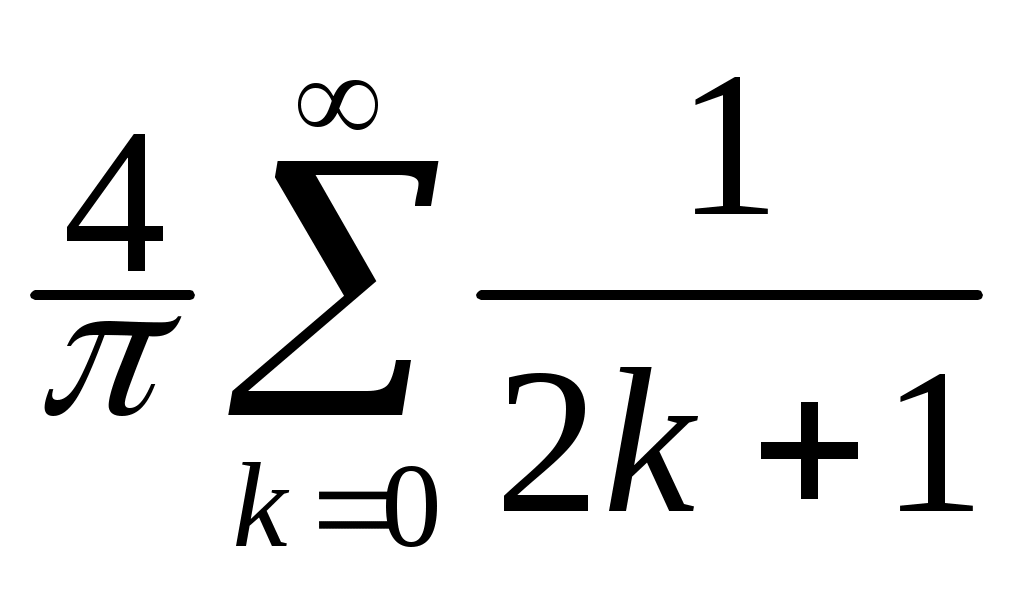 sin (( 2k + 1) x).
sin (( 2k + 1) x).
На интервале [–; ] ряд сходится к функции f(x), в точках х = 0 и х = – к нулю.
§ 5. Сдвиг основного промежутка.
Вся теория рядов Фурье излагалась для функций, заданных на отрезке [–; ], однако вместо этого отрезка можно было бы положить в основу рассуждения любой другой отрезок длины 2, так как 2 есть период всех функций системы 1, cos x, sin x, cos 2x, …, и справедлива
Теорема 9. Если функция f(x) имеет период 2, то интеграл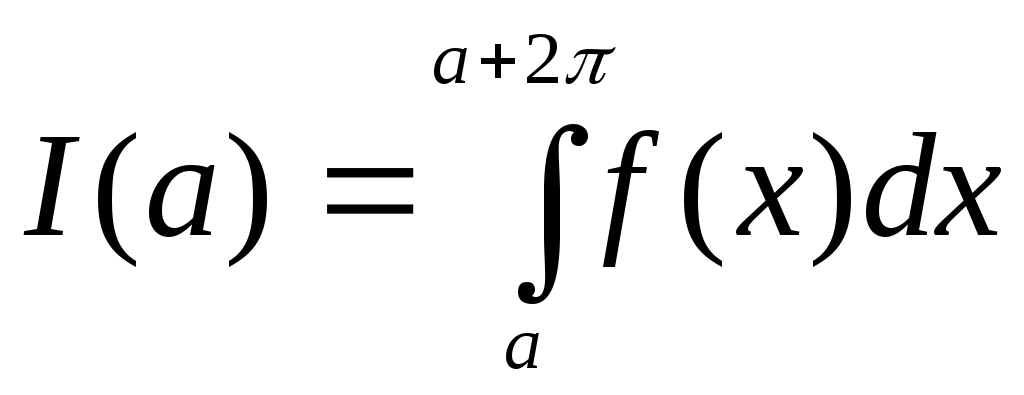 от числа а не зависит. Поэтому всю теорию можно перенести с отрезка [–; ] на любой отрезок [а, а+2].
от числа а не зависит. Поэтому всю теорию можно перенести с отрезка [–; ] на любой отрезок [а, а+2].
Теорема 10. Если f(x) дифференцируема на отрезке [0; 2], то всюду на открытом промежутке (0, 2) будет
f(x) =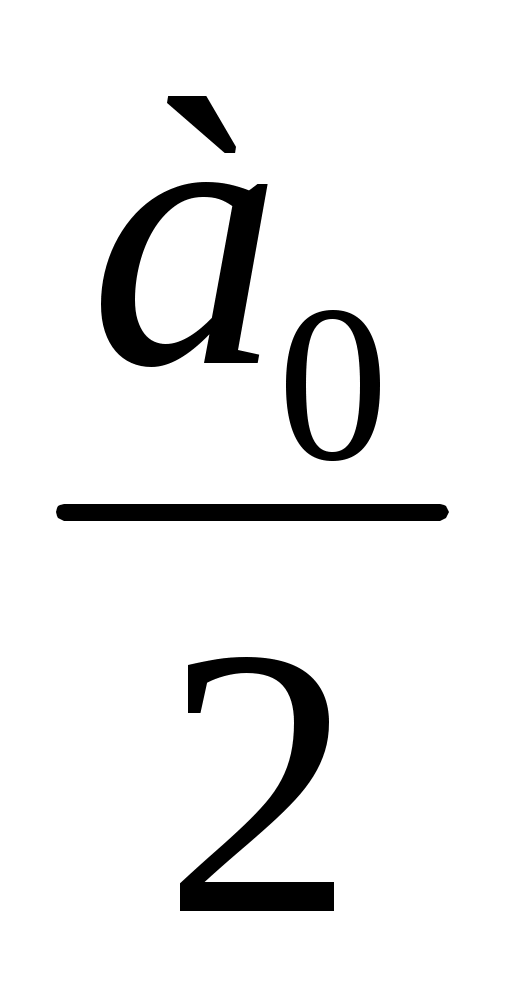 +
+ 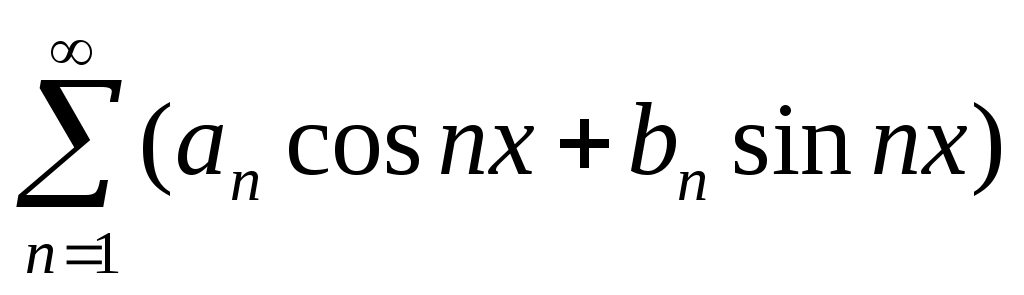
, где
а0 =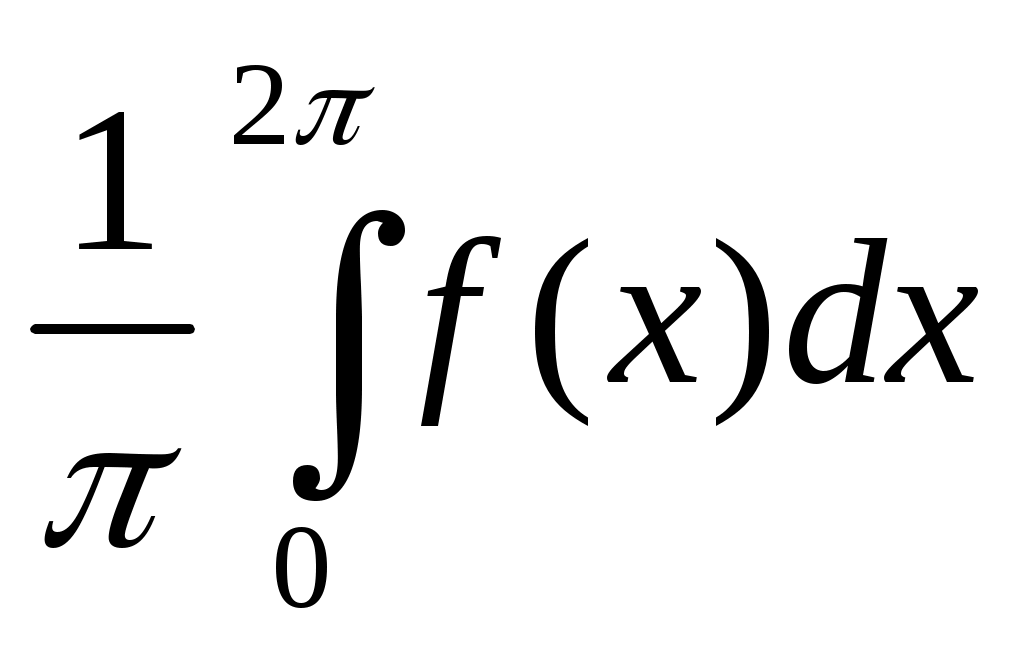 , (1.22)
, (1.22)
аn=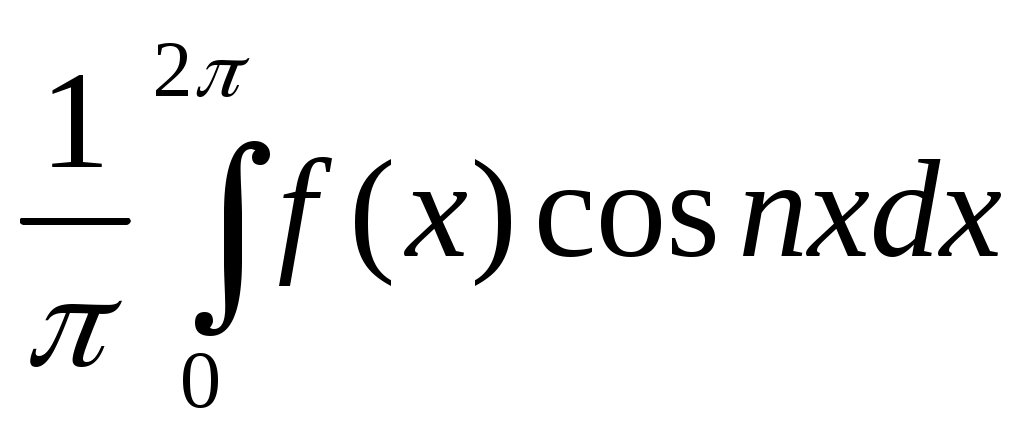 , (n=1,2,...); (1.23)
, (n=1,2,...); (1.23)
bn=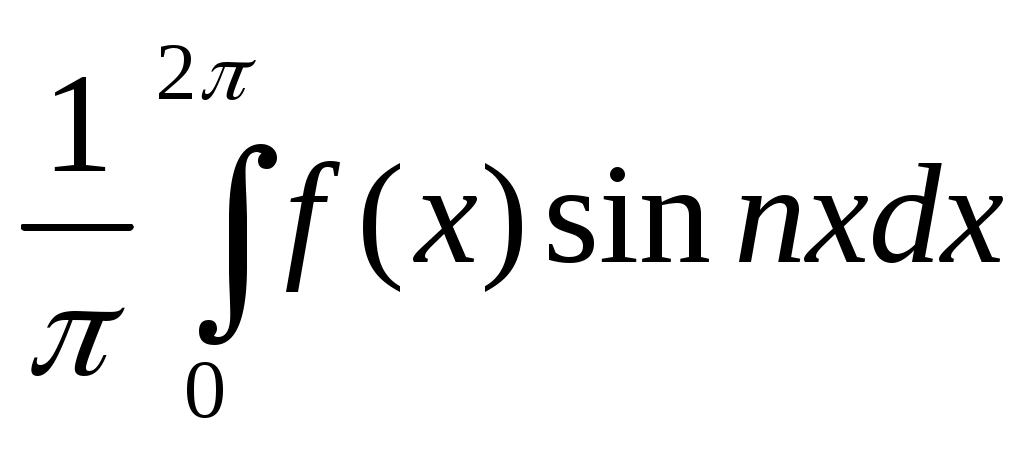 , (n=1,2,...); (1.24)
, (n=1,2,...); (1.24)
ряд сходится в точках x= 0, x= 2, где его сумма равна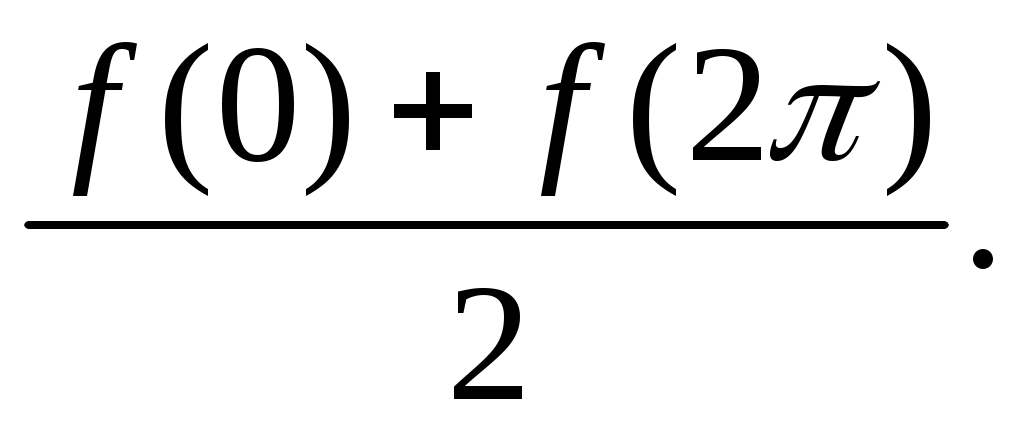
( без доказательства)
Пример 4. Разложить в ряд Фурье функцию f(x) = x, заданную на отрезке [0; 2].
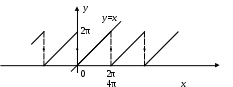
Рис. 5.
Решение:
График функции изобразим на рис. 5. Видно, что функция – разрывная. Найдем коэффициенты Фурье. Здесь
а0 =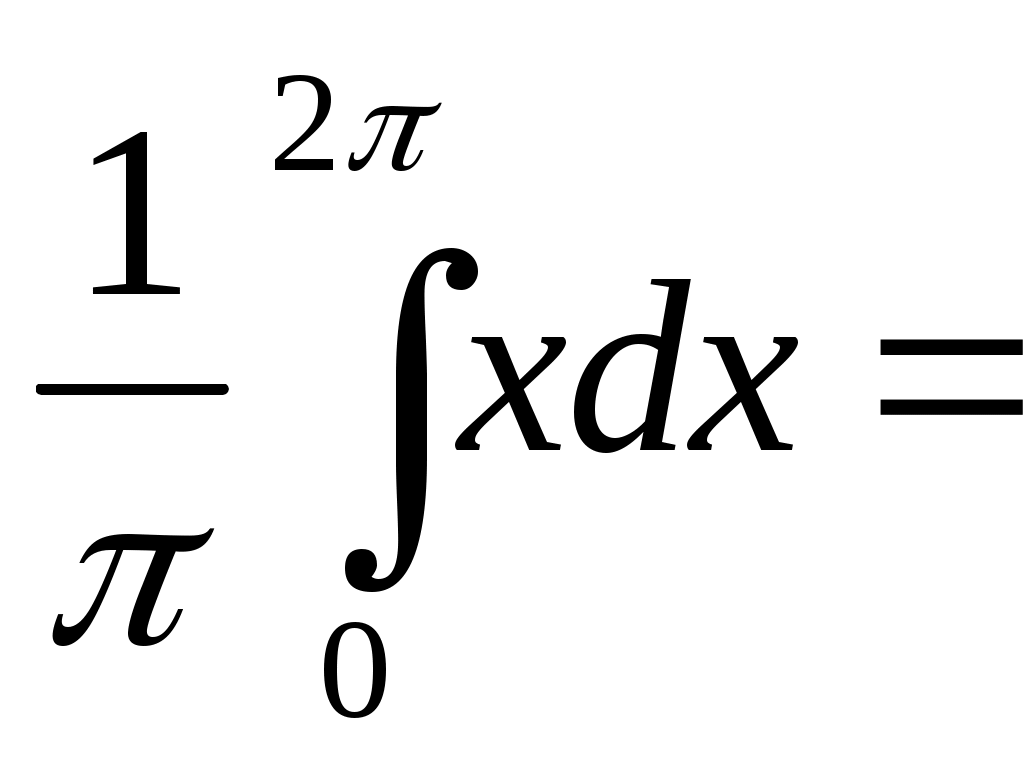
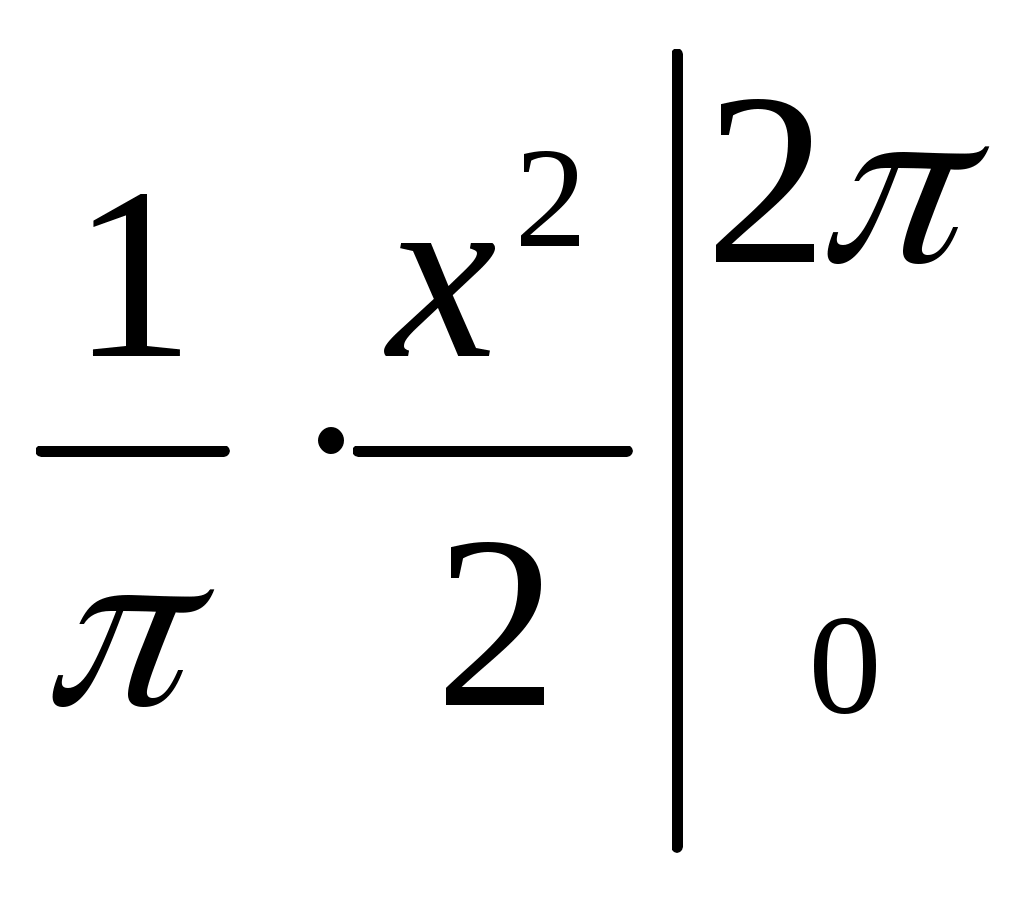 =
=  ,
,
аn =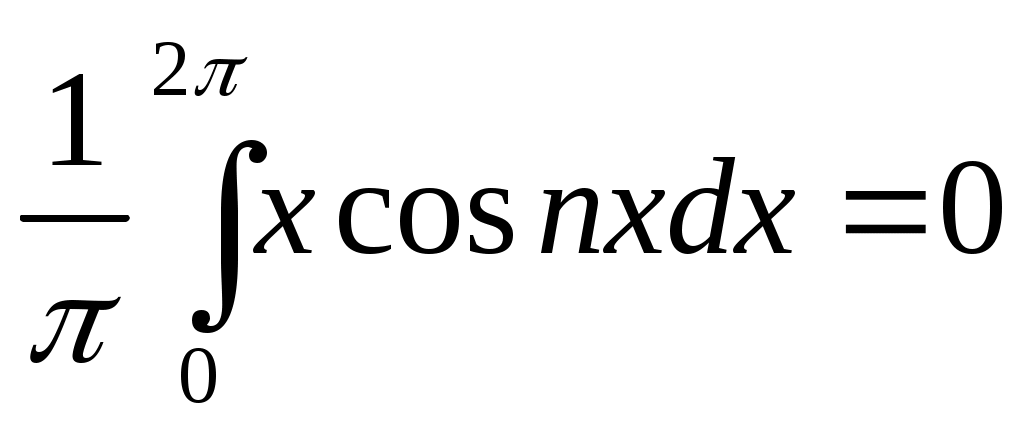 , (n=1,2,...),
, (n=1,2,...),
bn =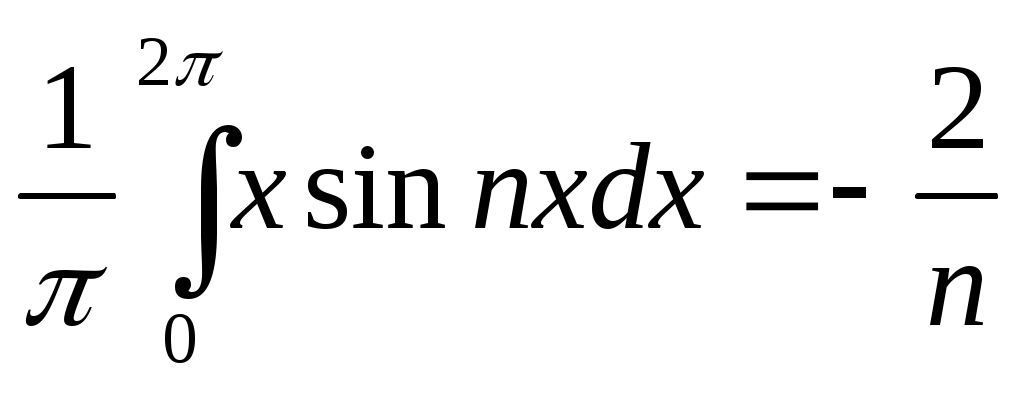 .
.
Стало быть, при 0 < x < 2π будет x =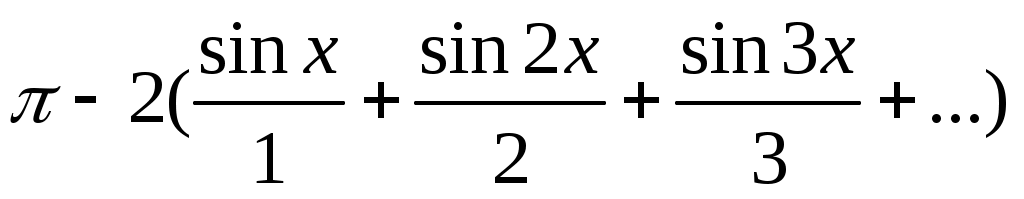 .
.
В точках x= 0 и x= 2 сумма S(x) ряда равна .
§ 6. Разложение в ряд Фурье функций с периодом 2ℓ.
Пусть функция f(x) задана и дифференцируема на отрезке [–l; l]. Положим φ(z) =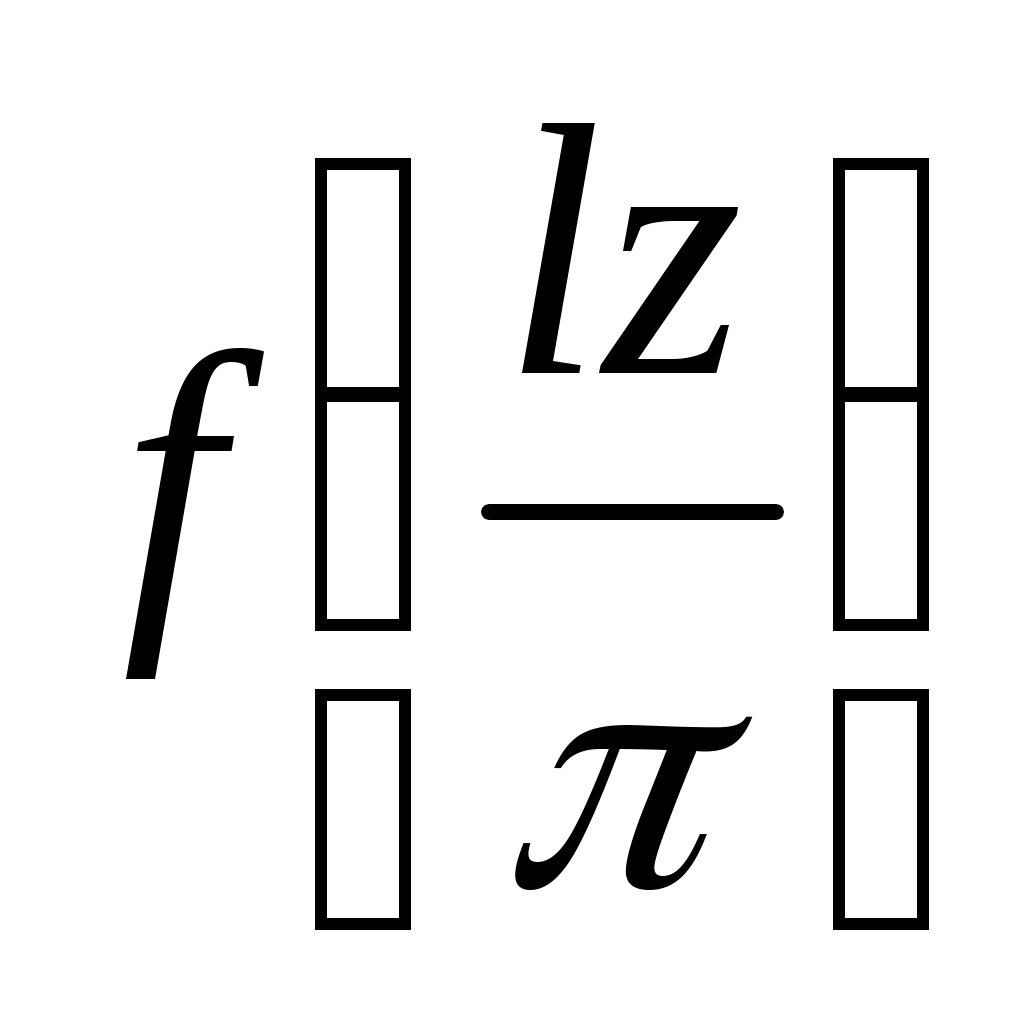 .
.
Тогда φ(z) будет заданной и дифференцируемой уже на отрезке [–π; π].Значит к φ(z) применима теория, изложенная выше, поэтому при – π < z< π будет
φ(x) =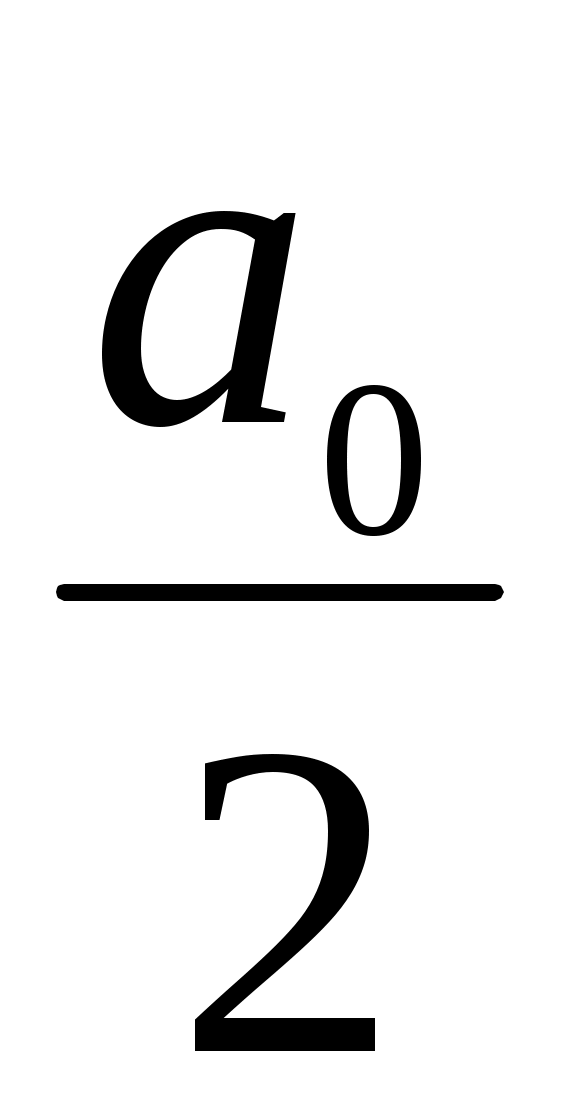 +
+ 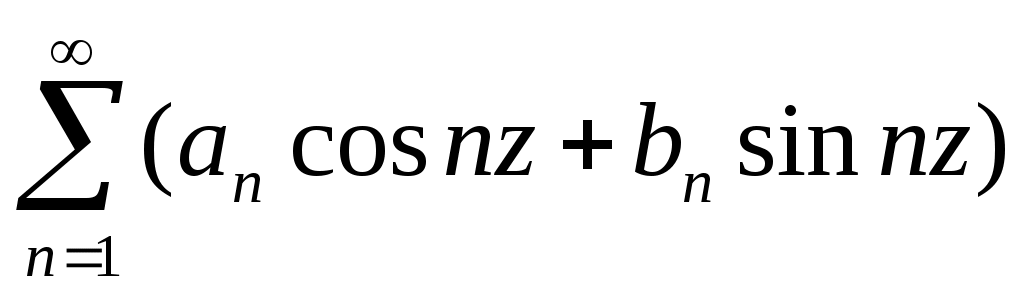 .
.
Положим в этом равенстве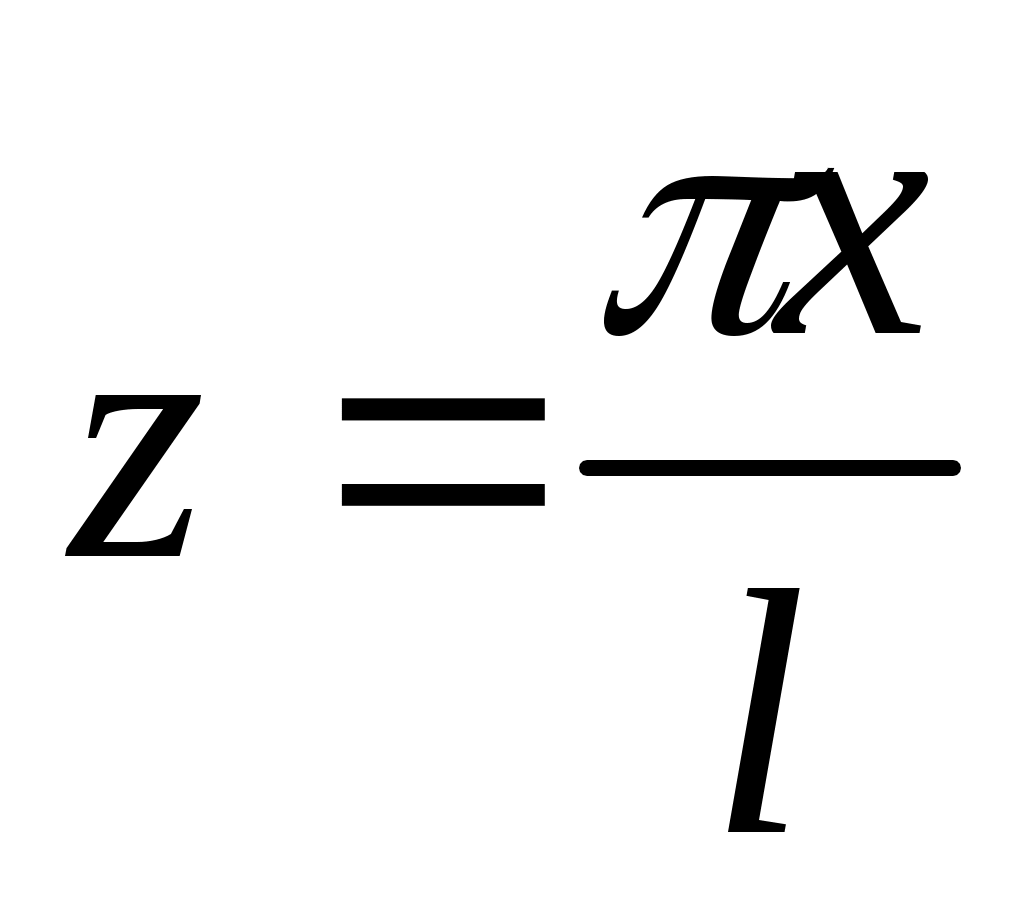 . Тогда для – l < x< l , то есть для функций с любым периодом 2ℓ разложение в ряд Фурье, когда оно возможно, и формулы для коэффициентов Фурье таковы:
. Тогда для – l < x< l , то есть для функций с любым периодом 2ℓ разложение в ряд Фурье, когда оно возможно, и формулы для коэффициентов Фурье таковы:
f(x) =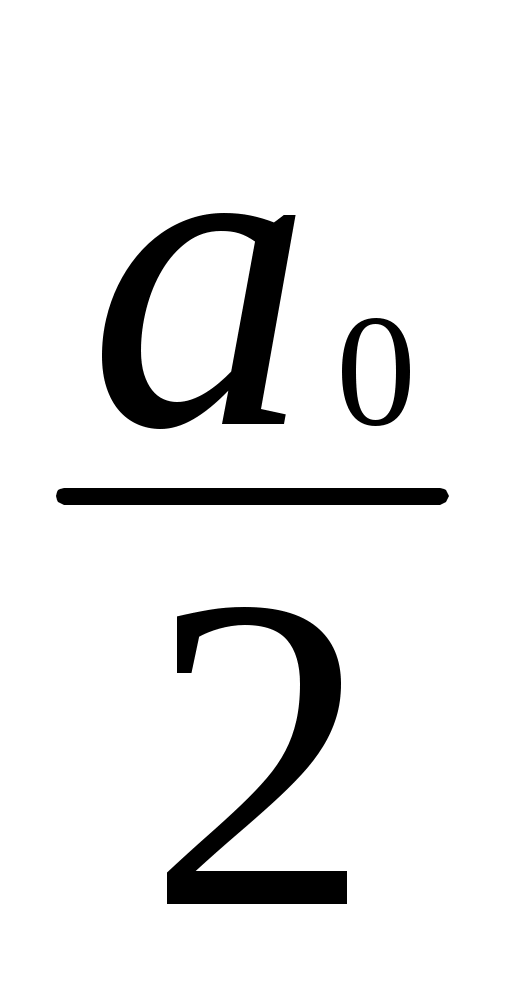 +
+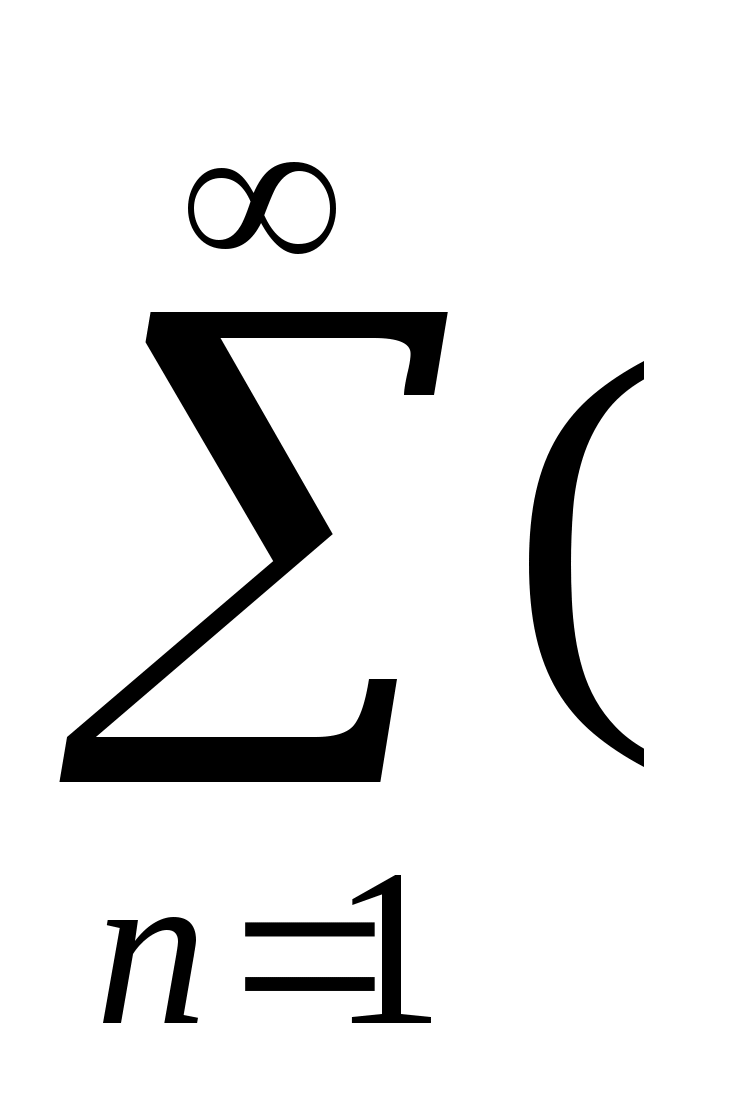
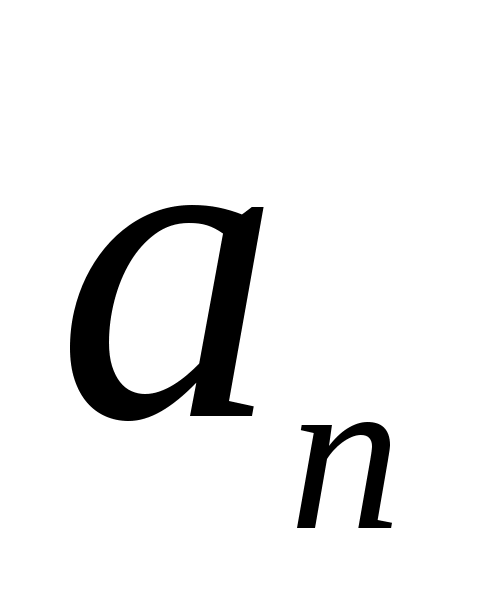 cos
cos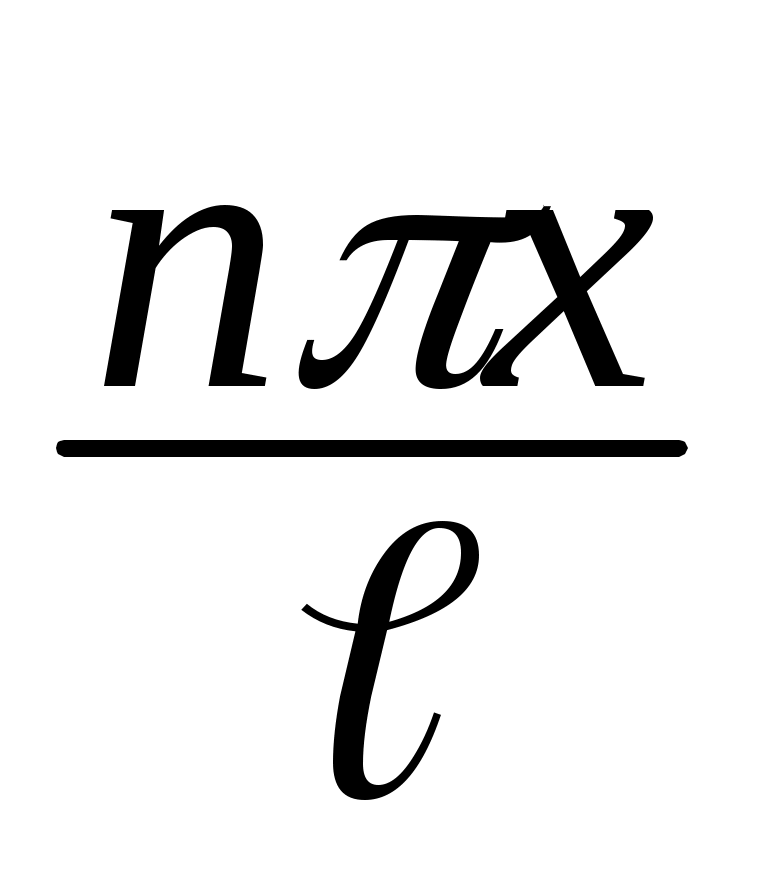 +
+ 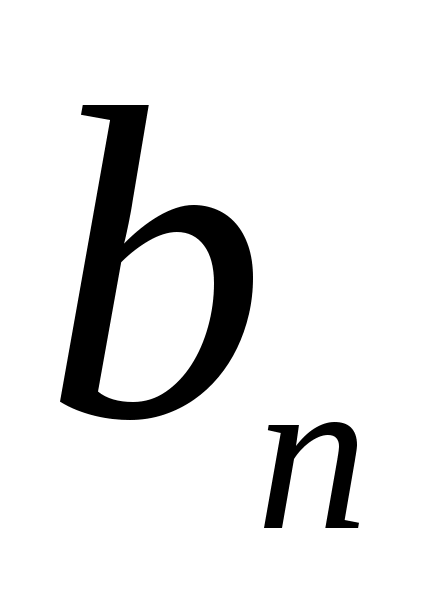 sin
sin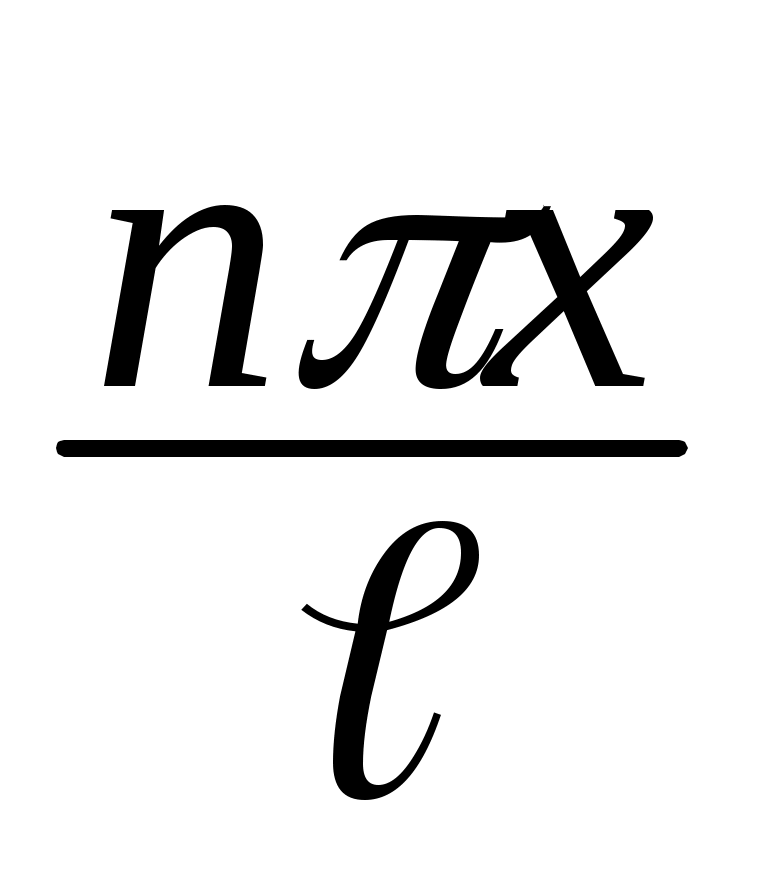 ), ( 1.25 )
), ( 1.25 )
где а0 =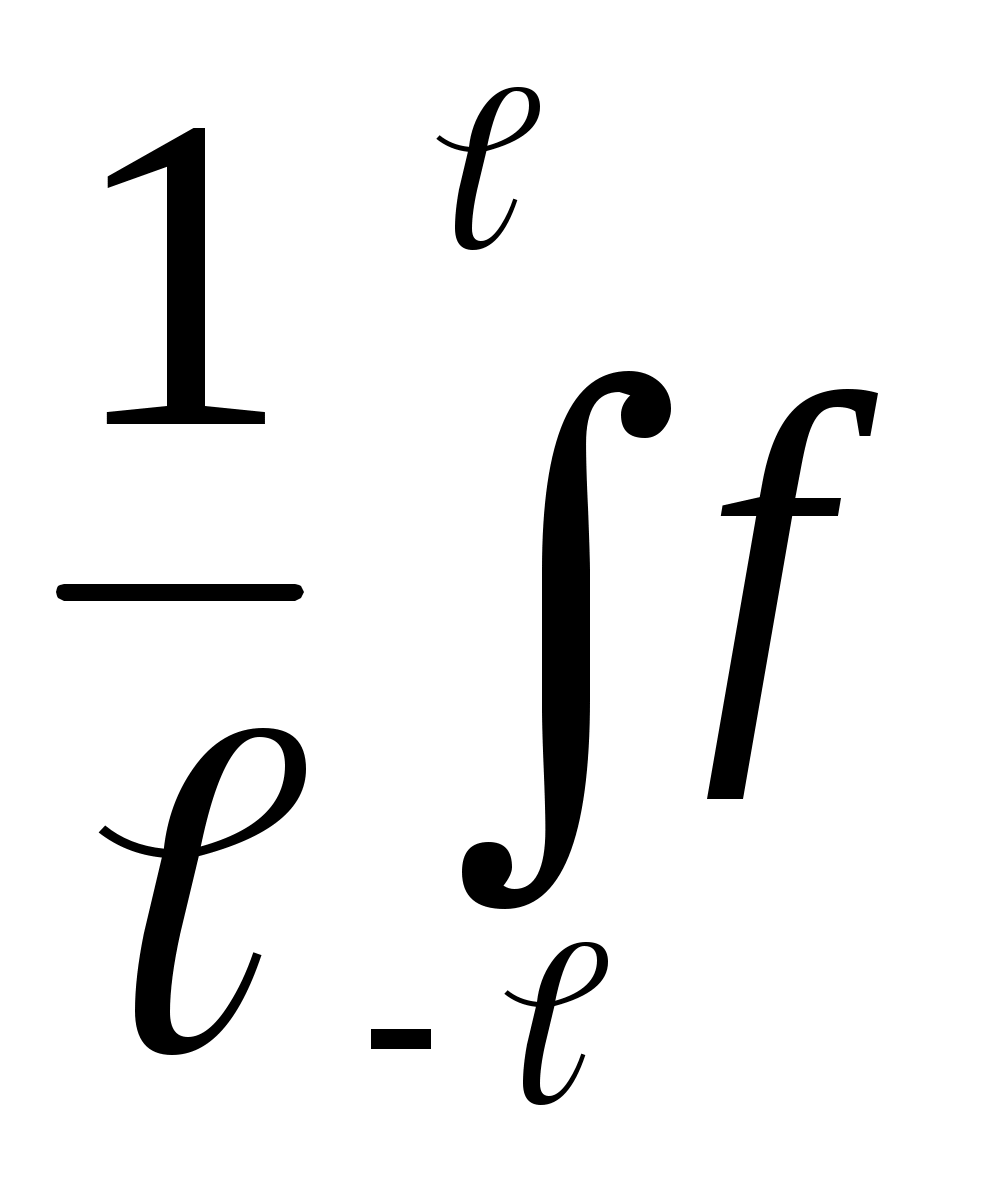 (x)dx; аn=
(x)dx; аn= 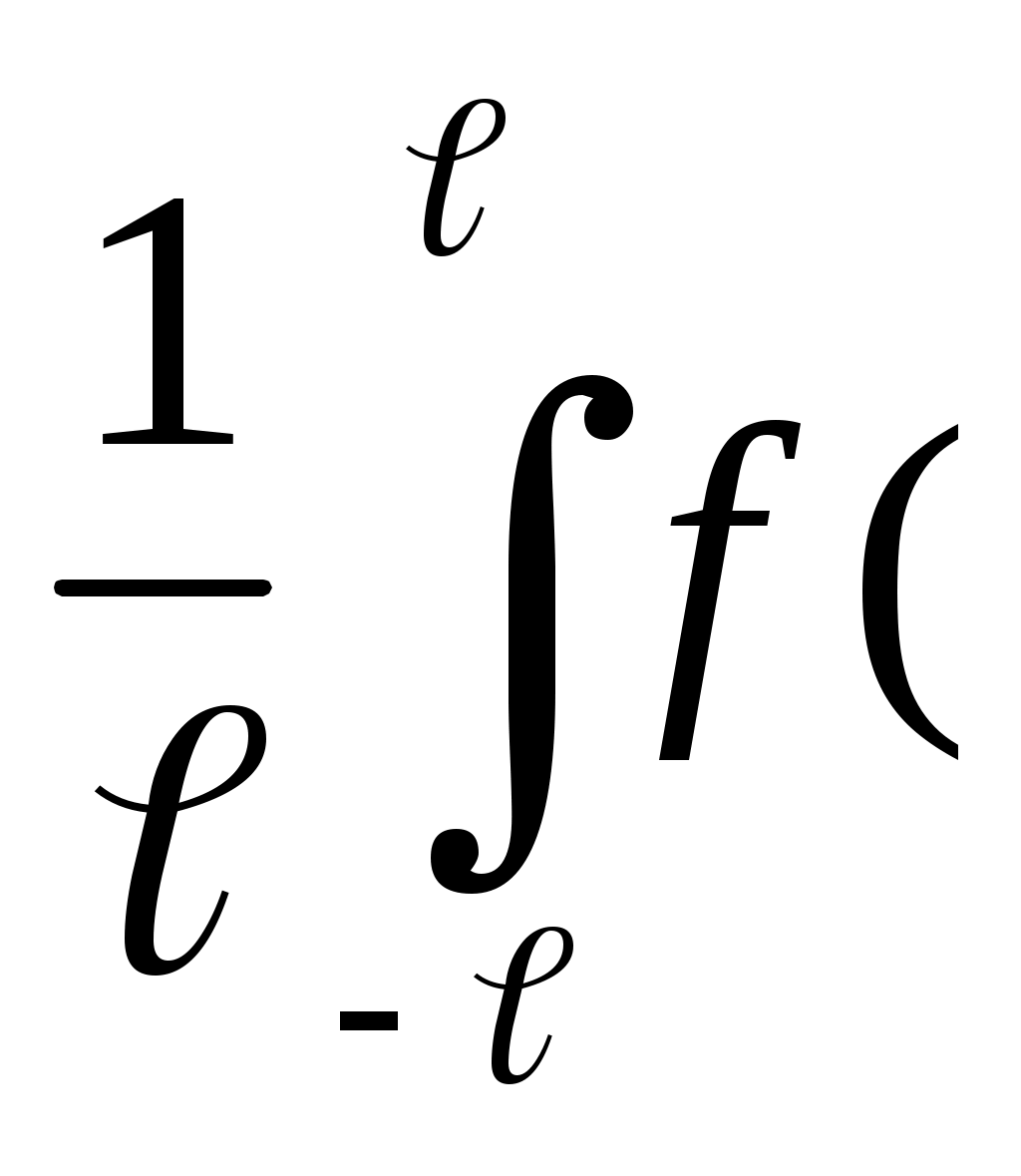 x) cos
x) cos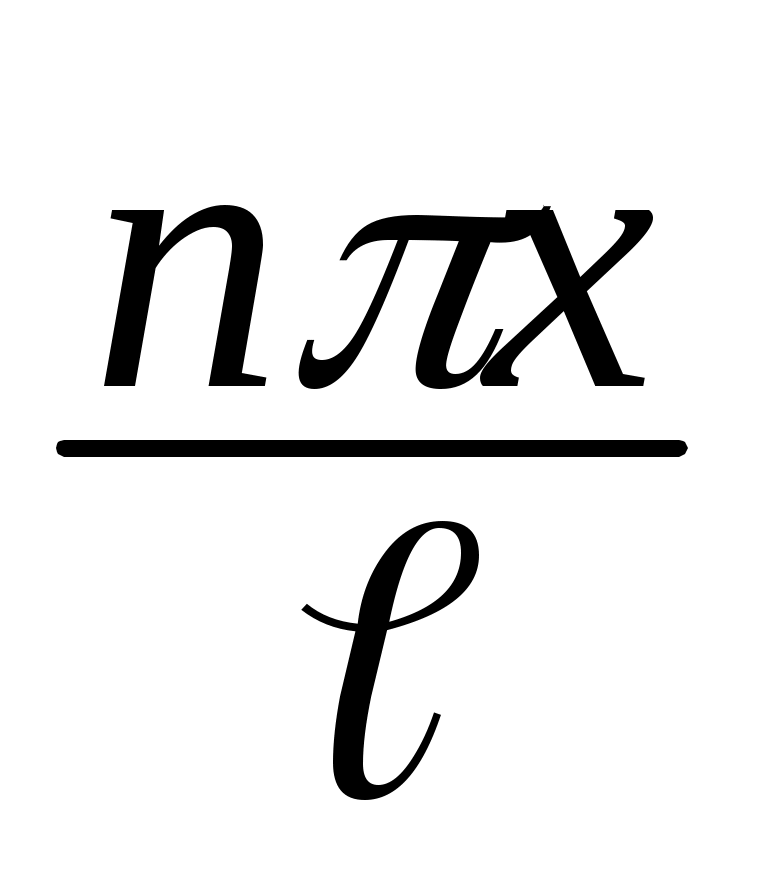 dx; bn=
dx; bn= 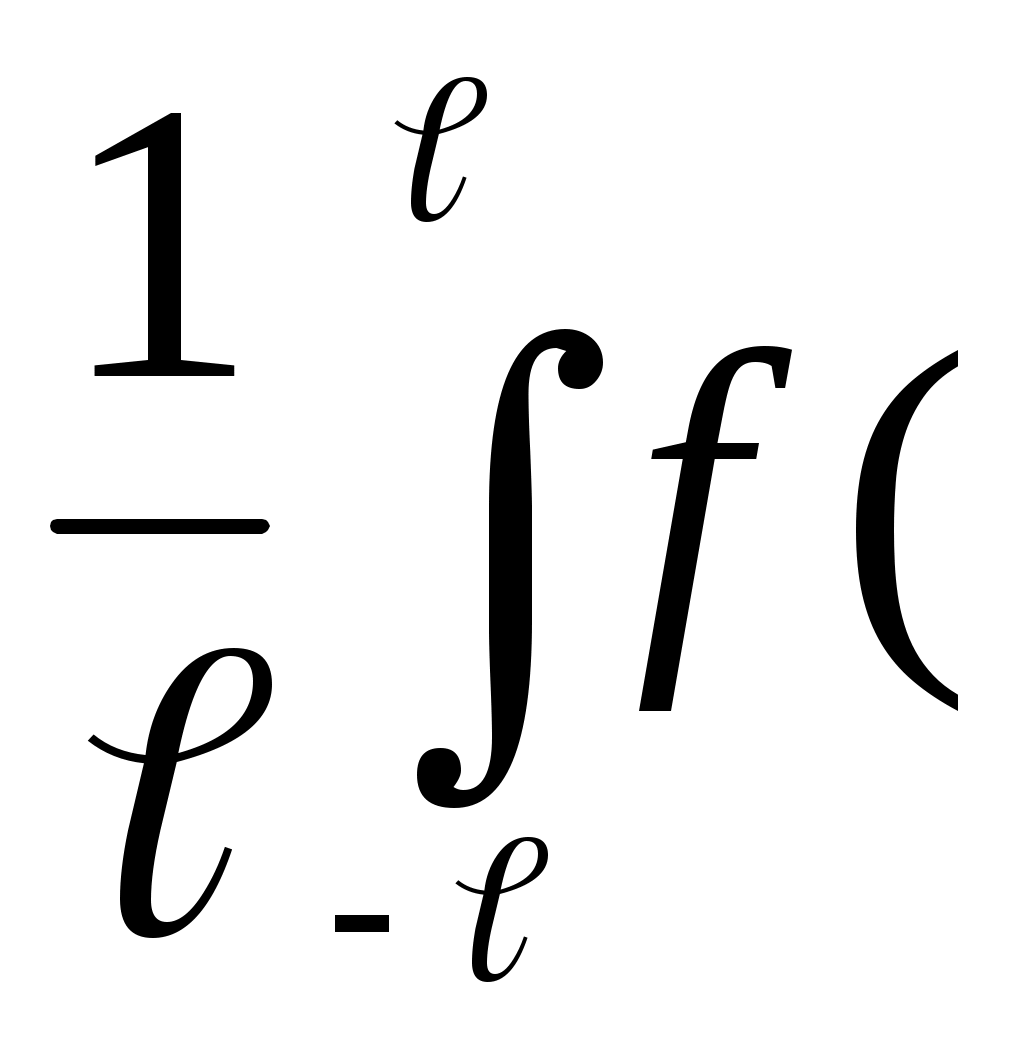 x) sin
x) sin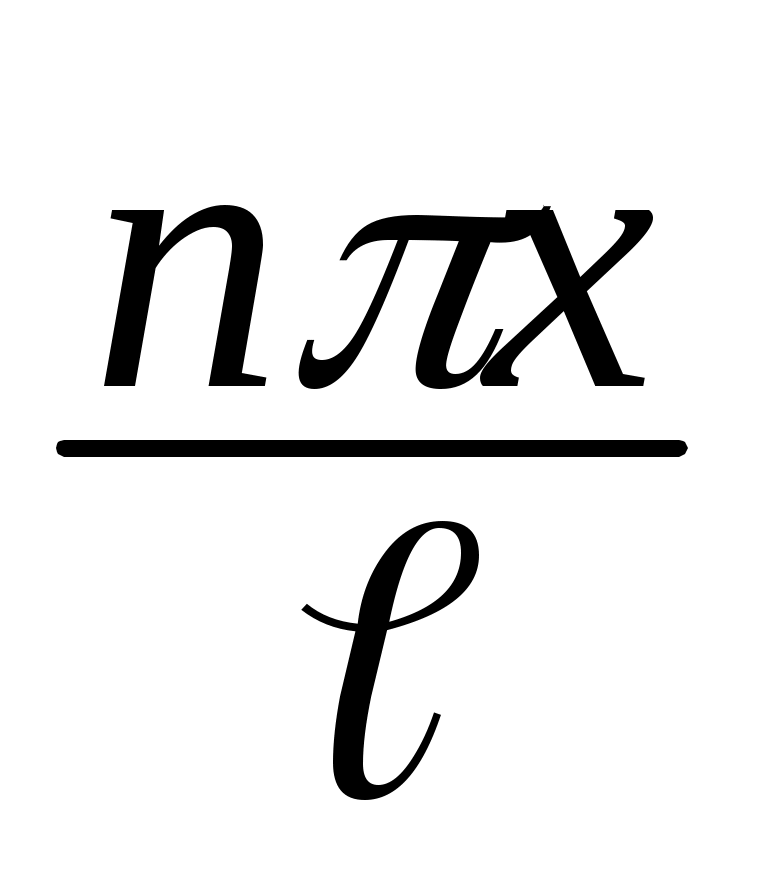 dx (1.26)
dx (1.26)
Если f(x) – четная, то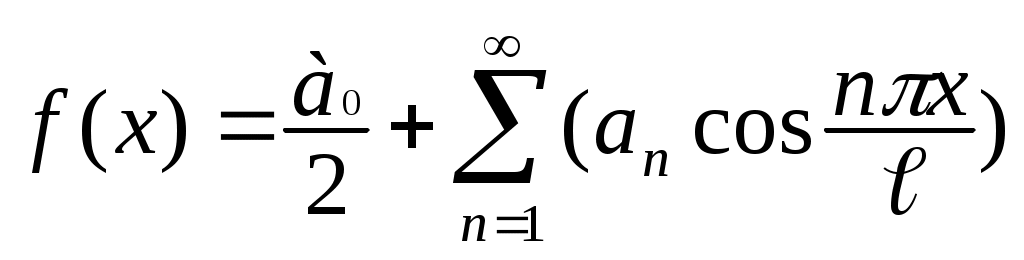 , (1.27)
, (1.27)
где а0 =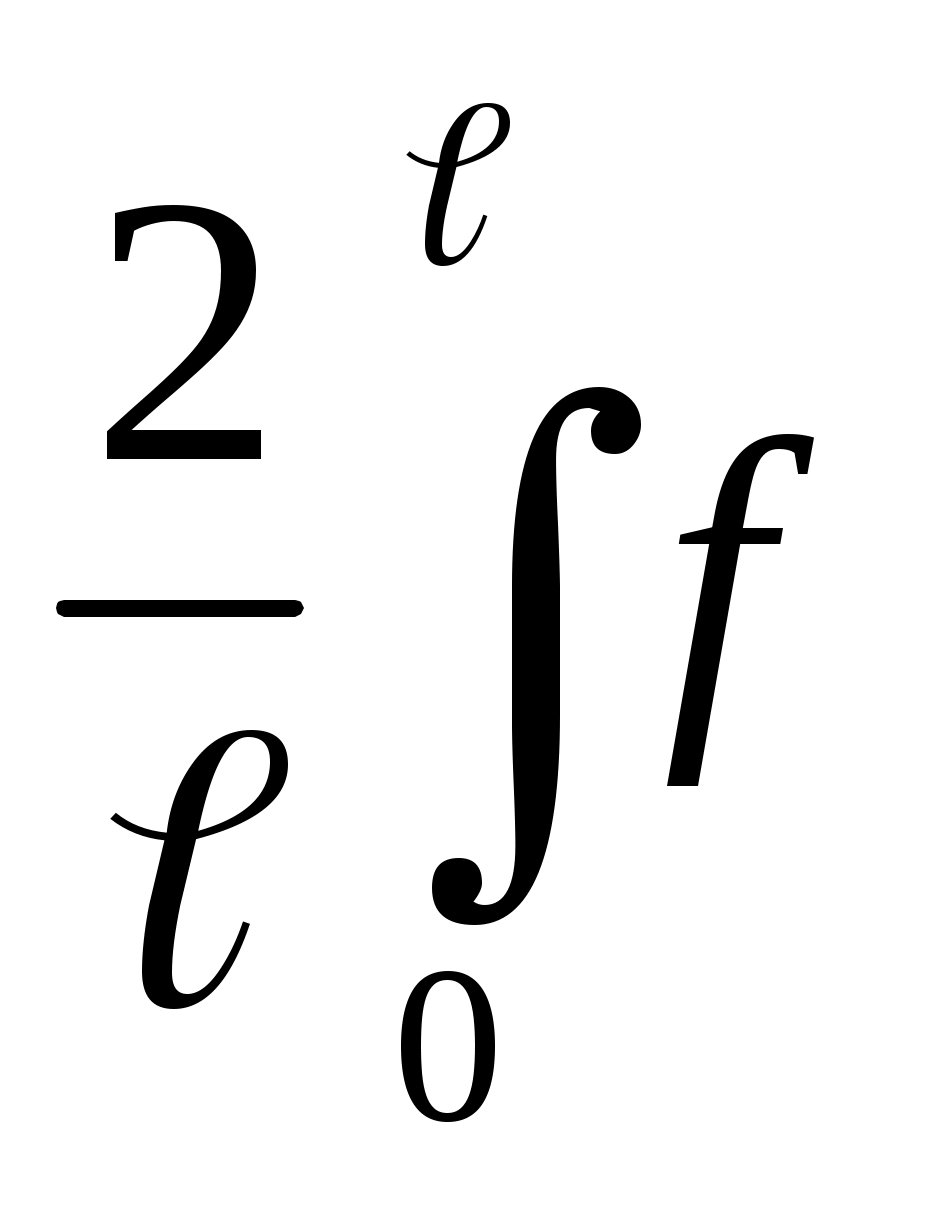 (x)dx; аn=
(x)dx; аn= 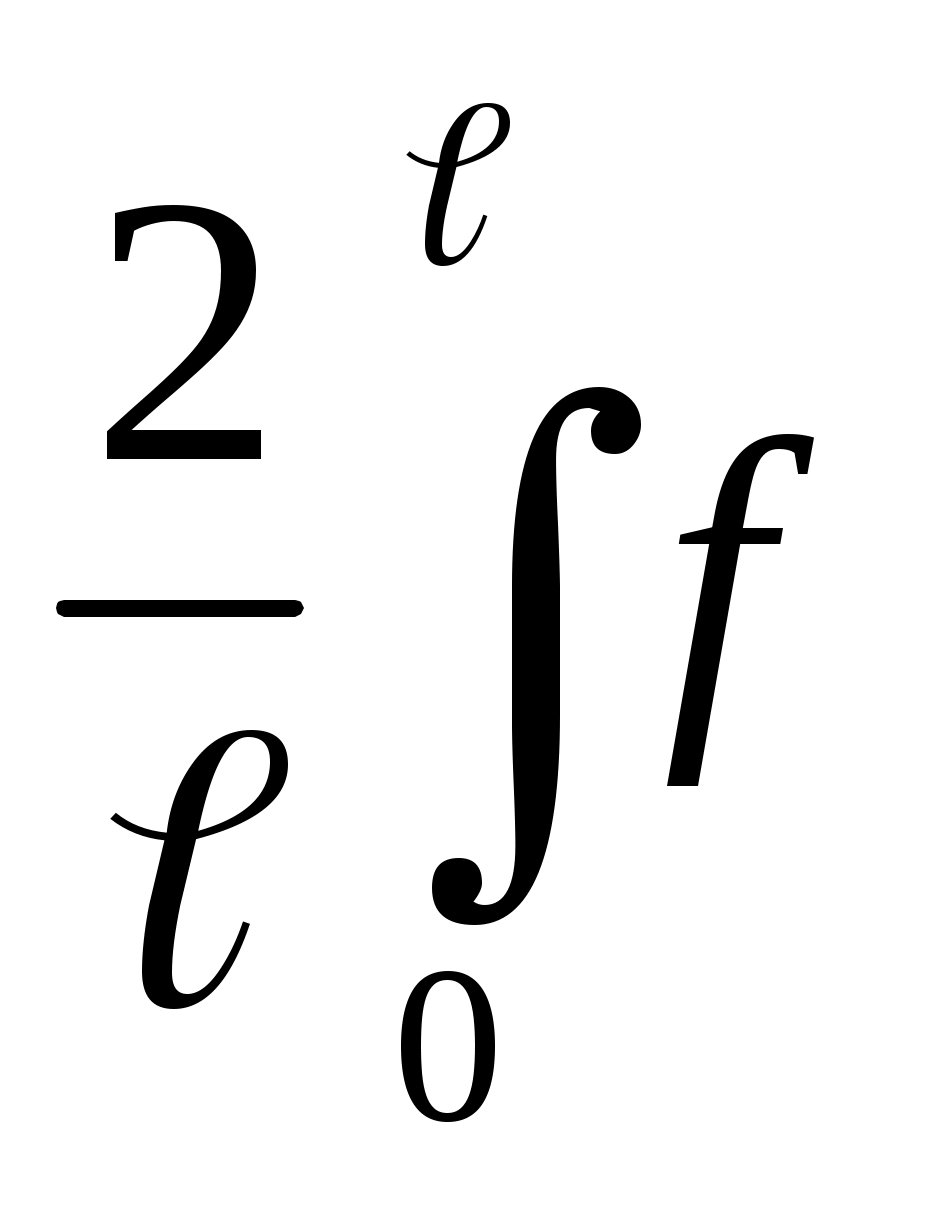 (x) cos
(x) cos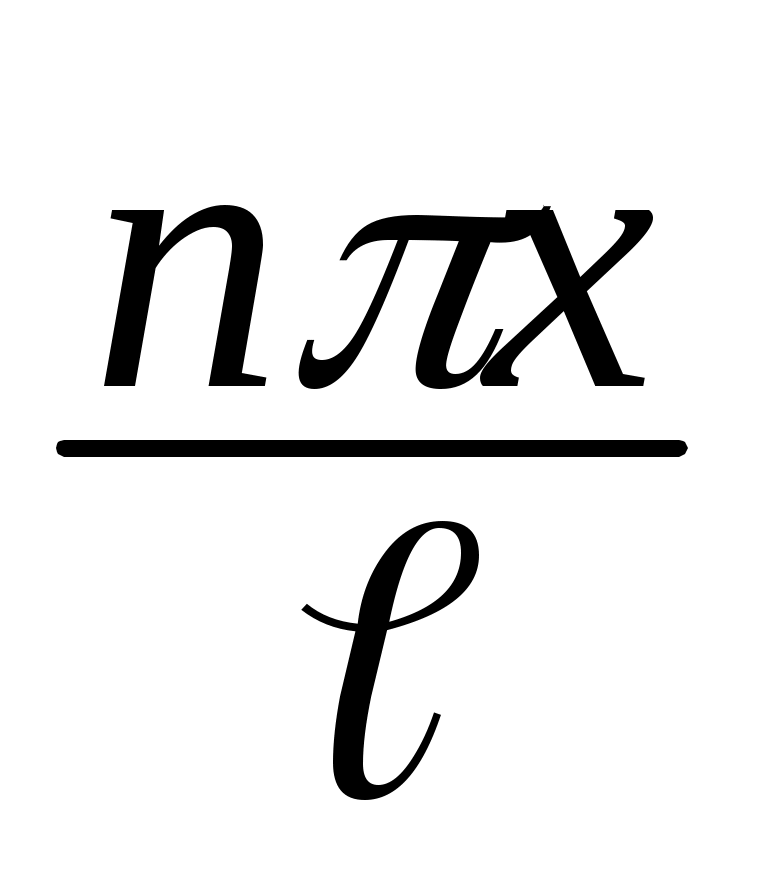 dx . (1.28)
dx . (1.28)
Если f(x) – нечетная, то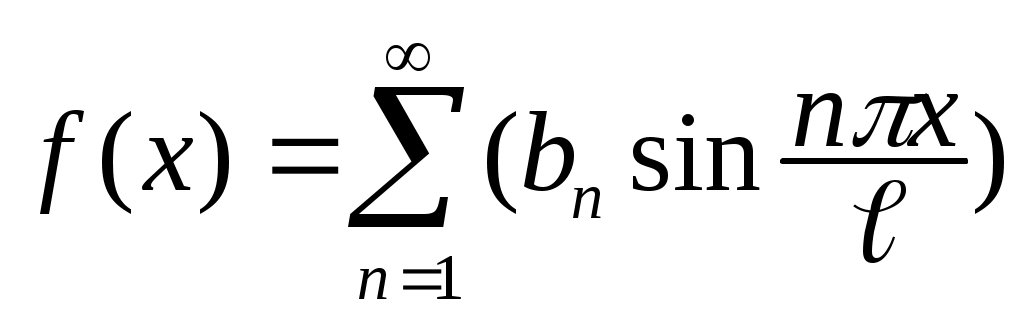 , (1.29)
, (1.29)
где bn=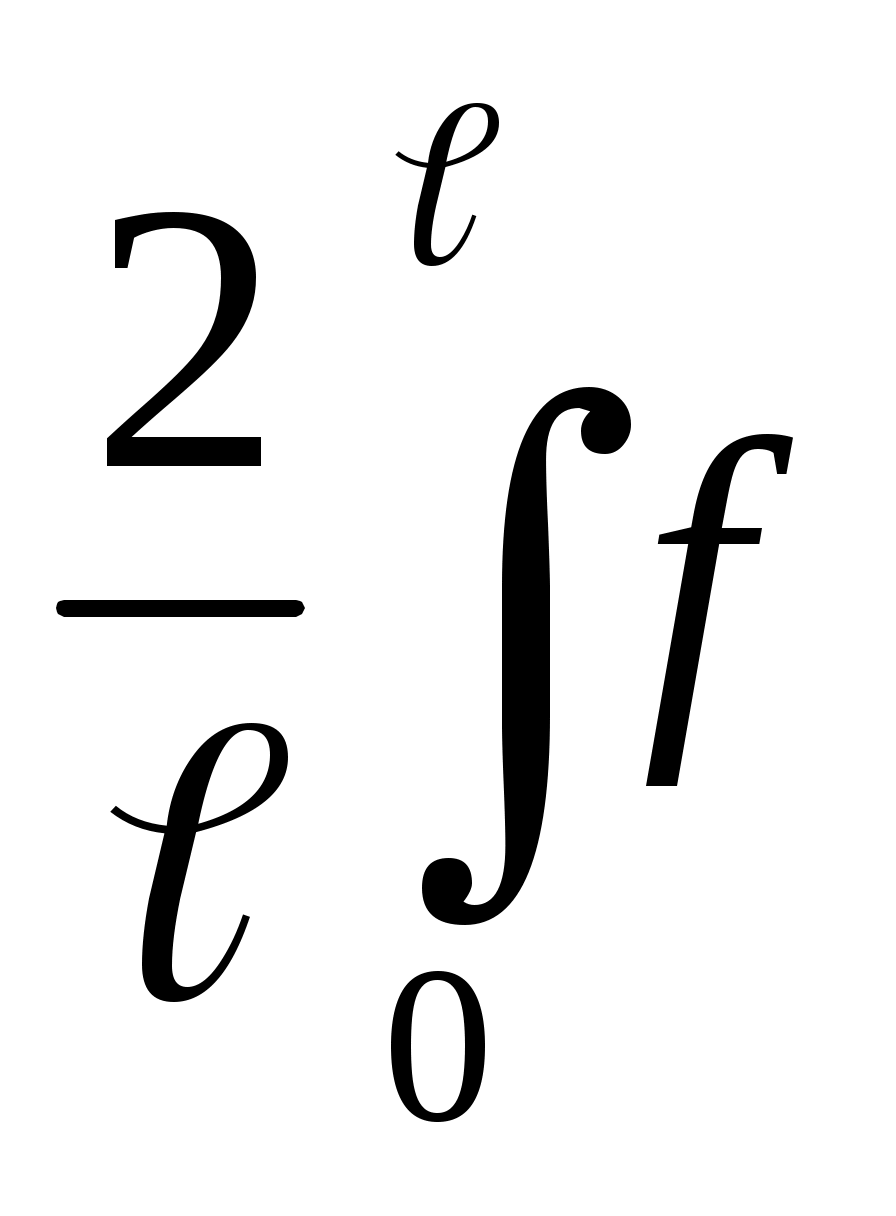 (x) sin
(x) sin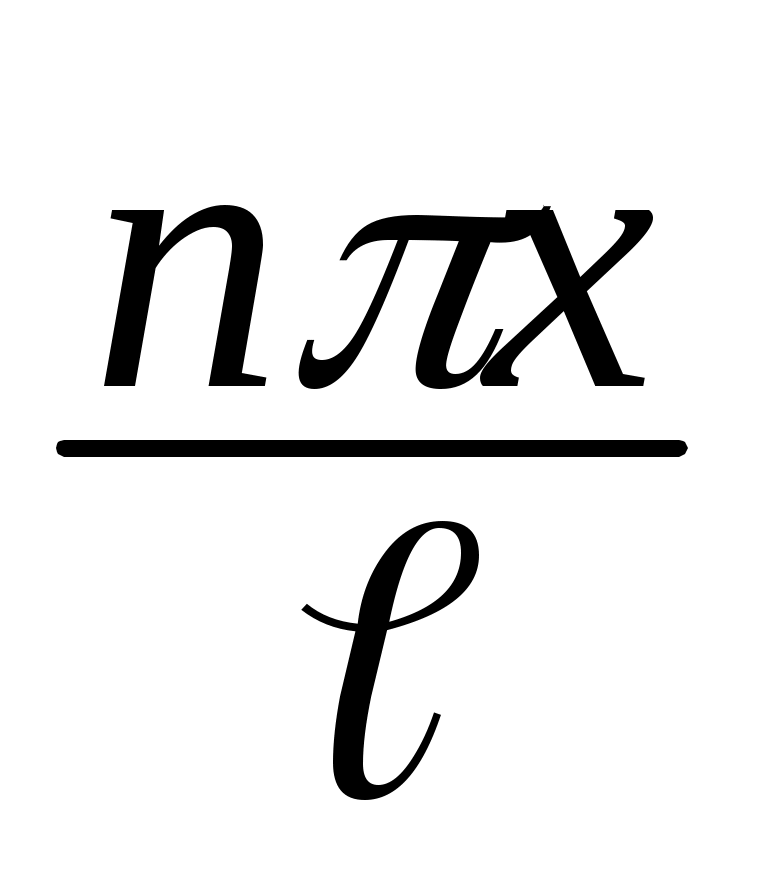 dx. (1.30)
dx. (1.30)
Замечание. Можно от периода 2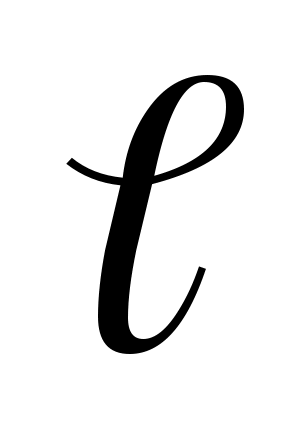 перейти к периоду 2, произведя замену переменной по формуле х =
перейти к периоду 2, произведя замену переменной по формуле х = 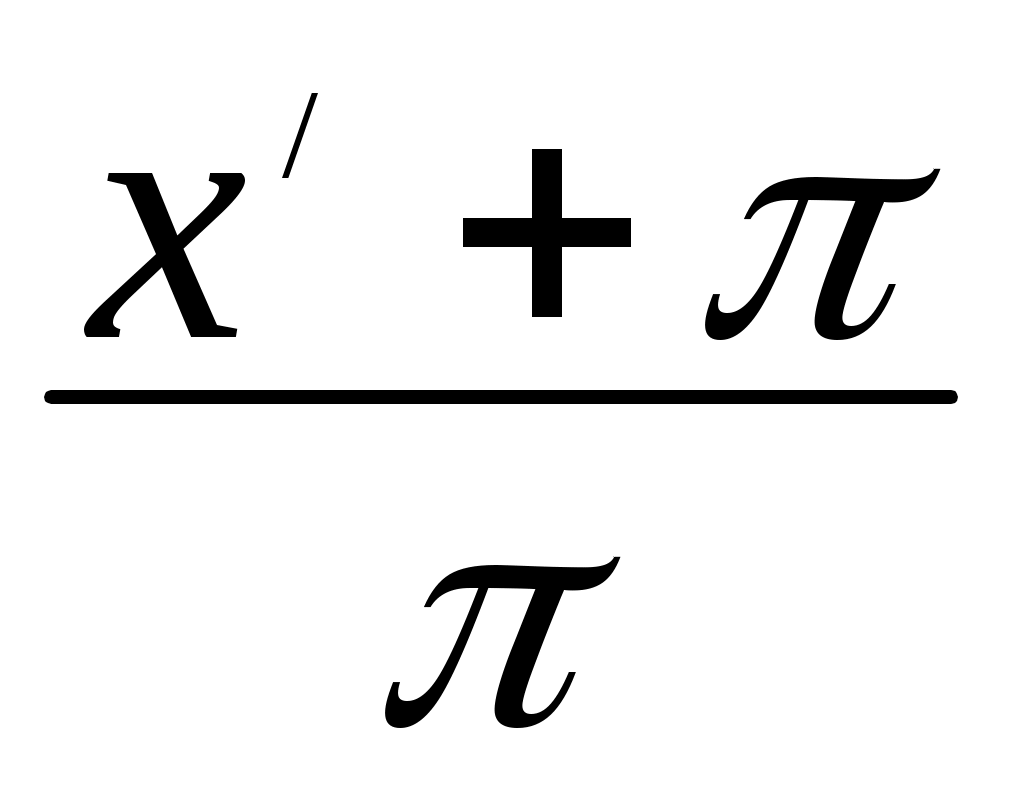 или х/ = (x–l) и затем вычислять коэффициенты Фурье для 2 - периодических функций.
или х/ = (x–l) и затем вычислять коэффициенты Фурье для 2 - периодических функций.
Пример 5. Разложить в ряд Фурье функцию f(x) = x, заданную на интервале –2 х 2.
Решение:
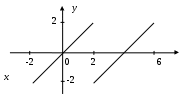
Рис. 6
График функции f(x) =
x изображен на рисунке 6. Видно, что функция нечетная с периодом 2ℓ = 4, то есть ℓ = 2. Найдем коэффициенты Фурье по формуле 1.30.
bn=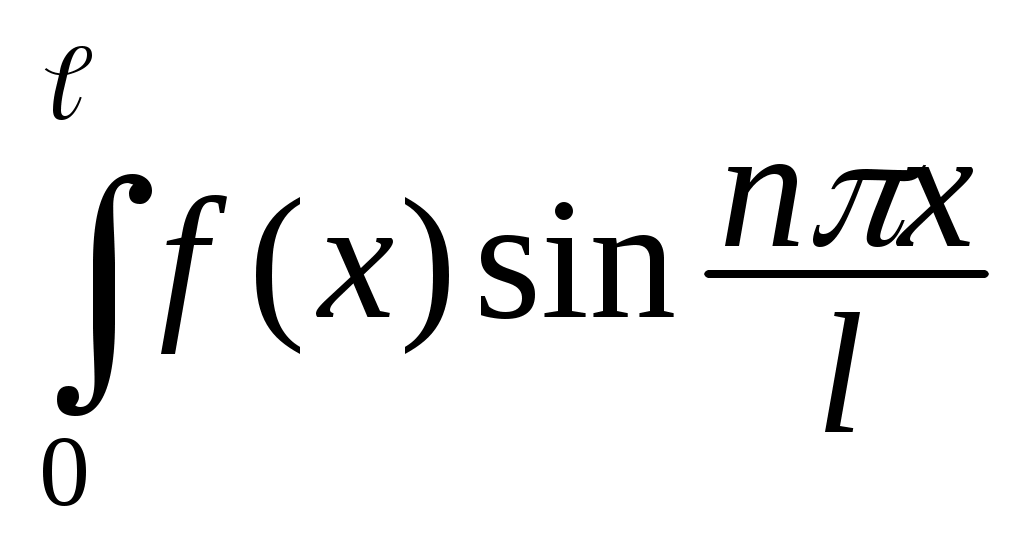 dx=
dx= 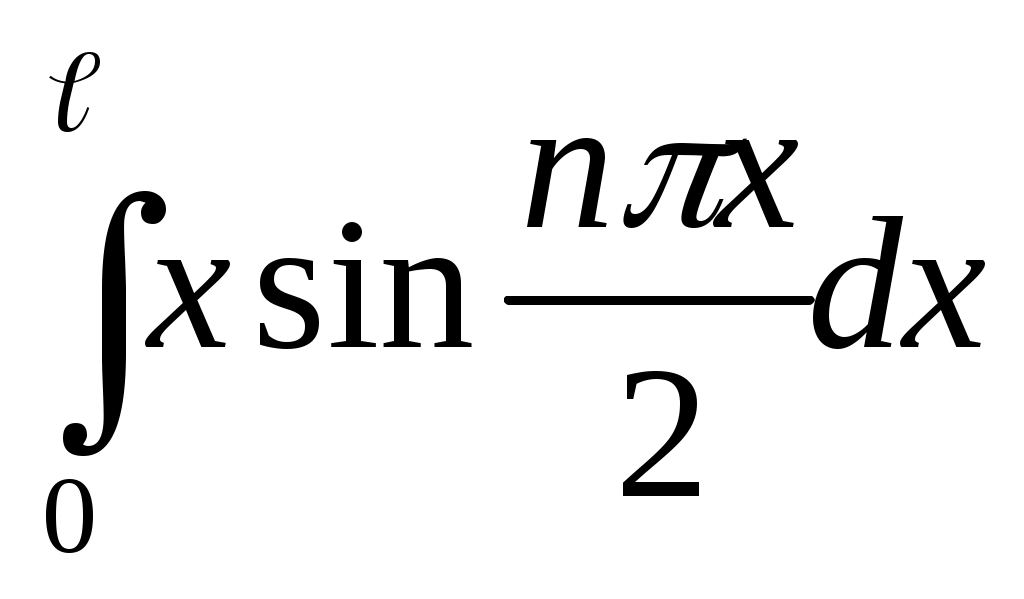 = –
= –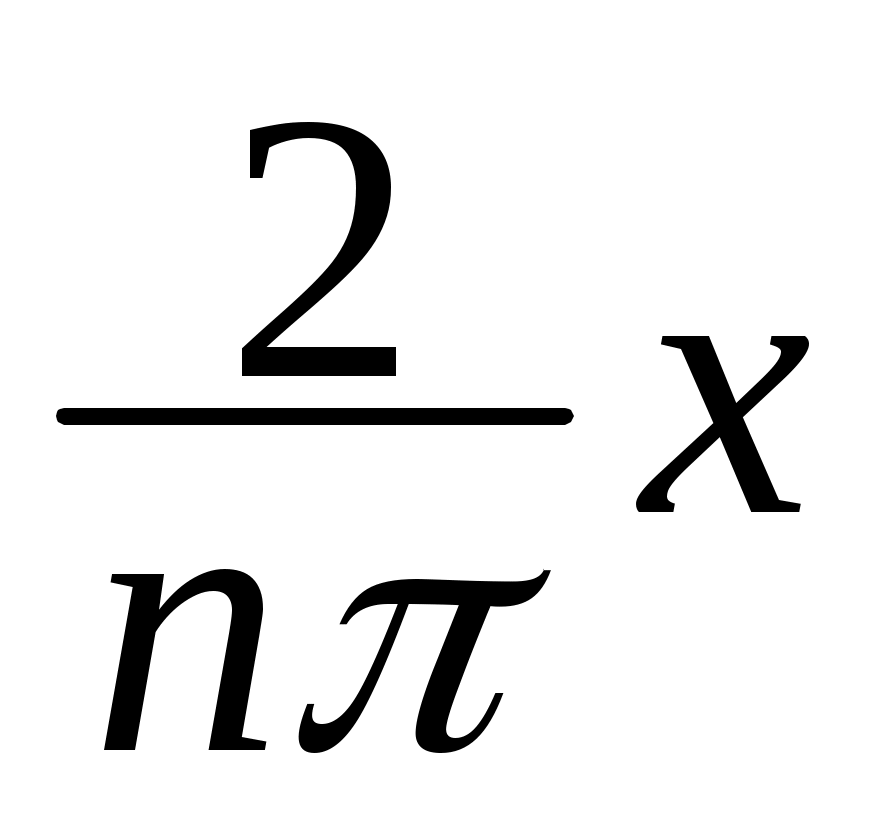 х cos
х cos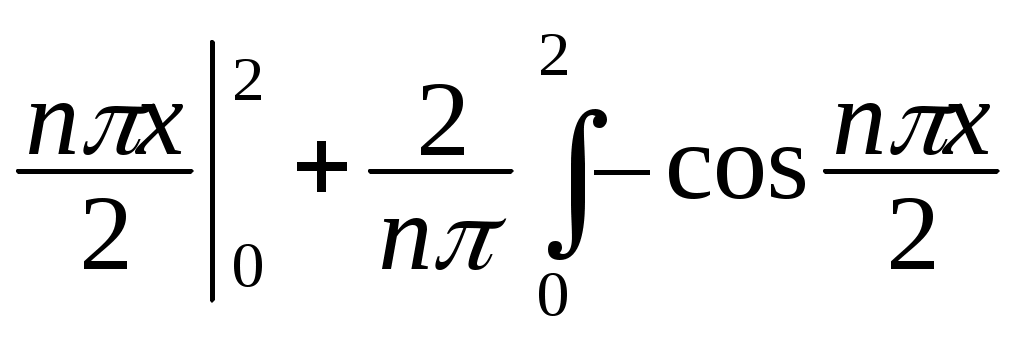 dx =
dx =
= –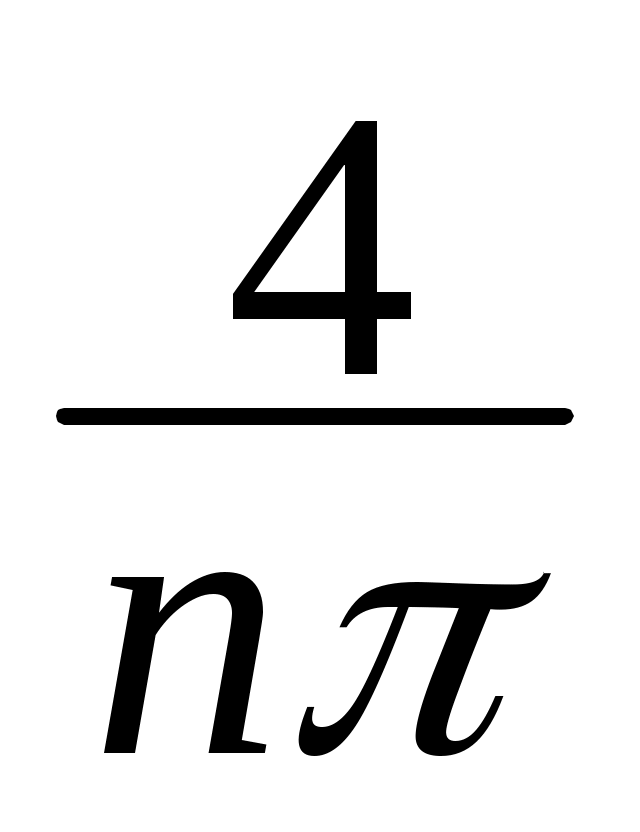 cos n +
cos n + 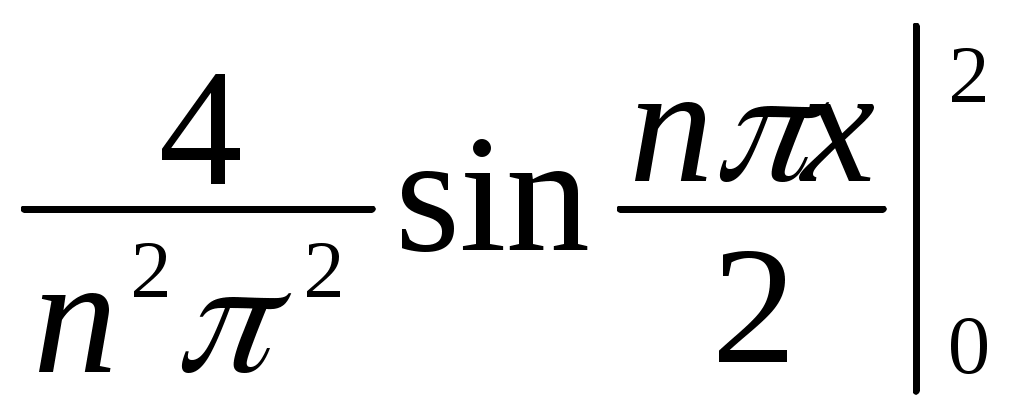 = –
= –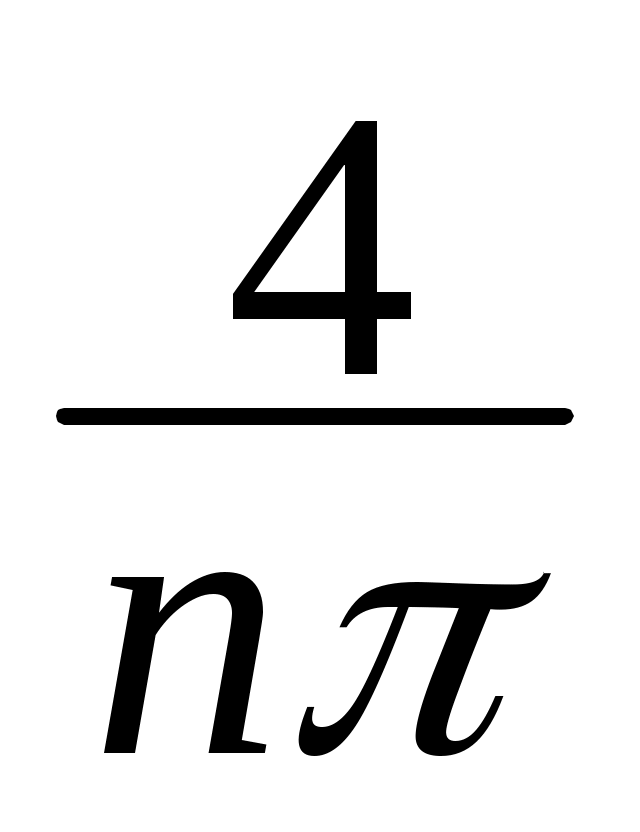 cos n +
cos n + 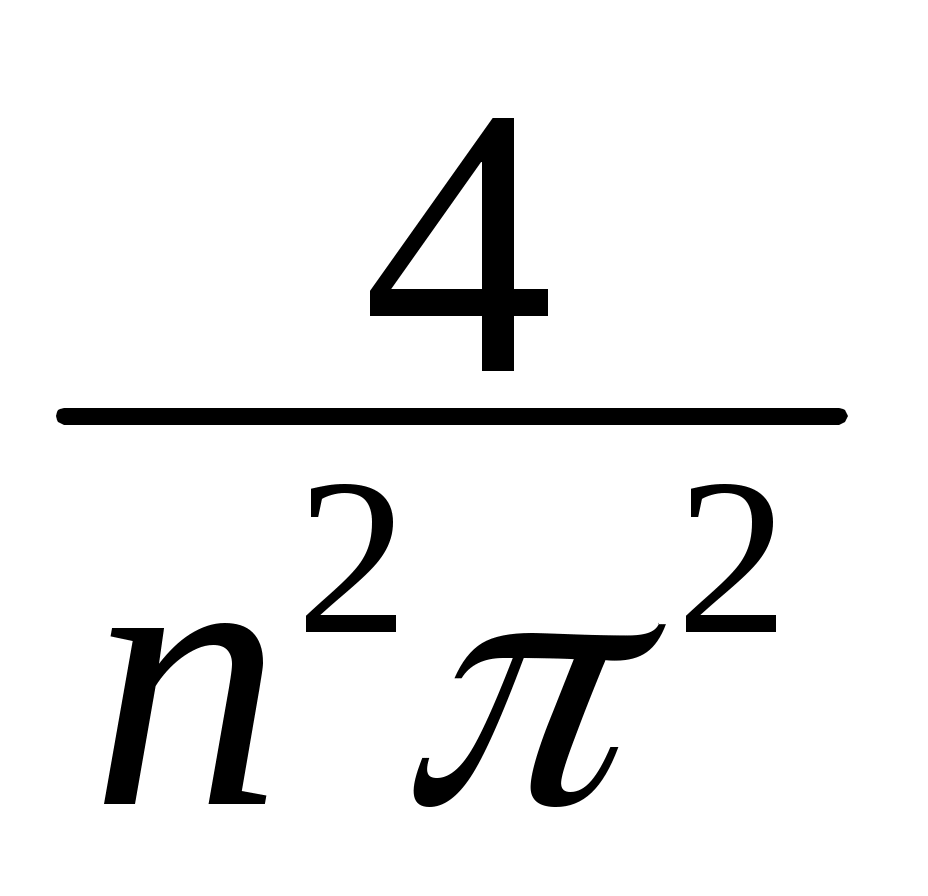 sin n = –
sin n = –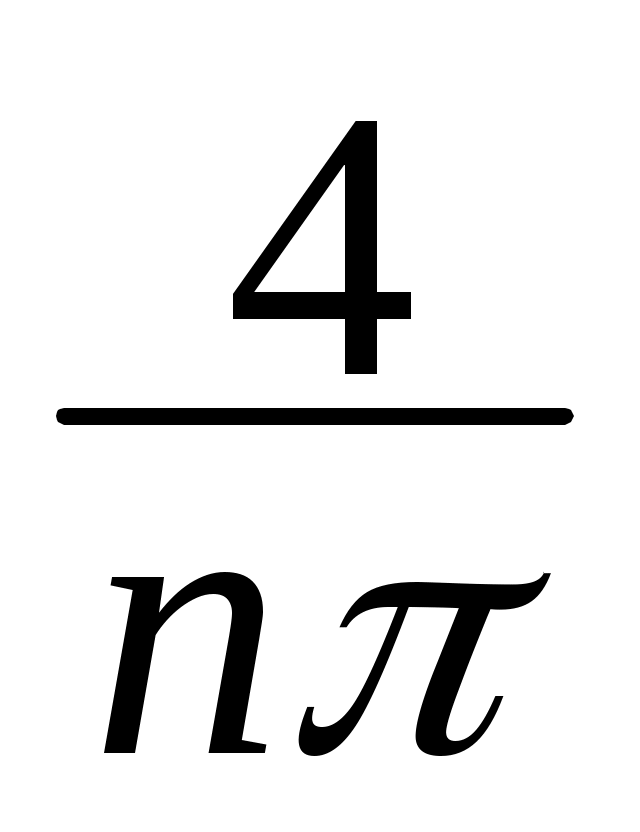 cos n =
cos n =
=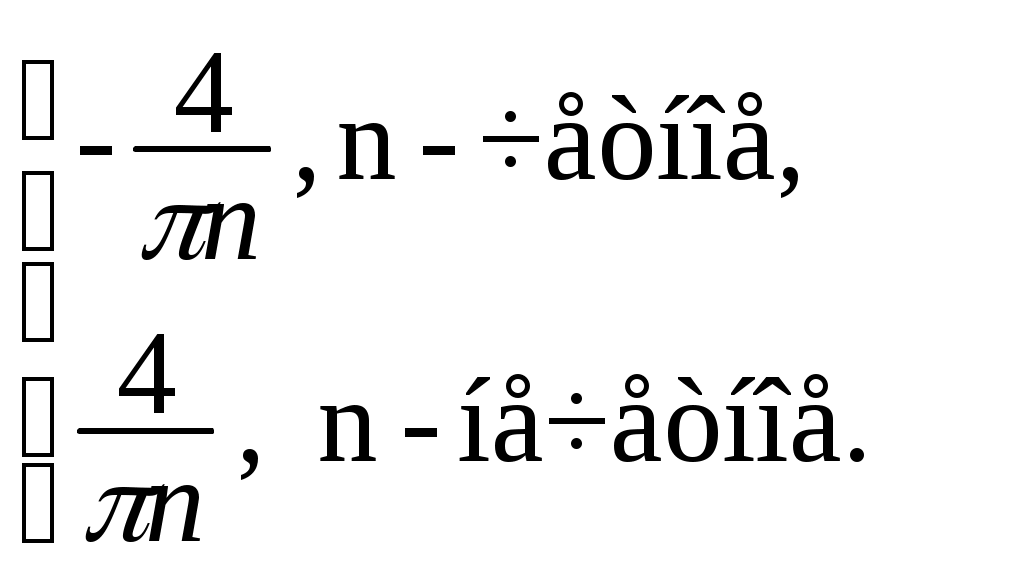
Следовательно, по 1.29 разложение в ряд Фурье функции f(x) имеет вид:
f(x) = x =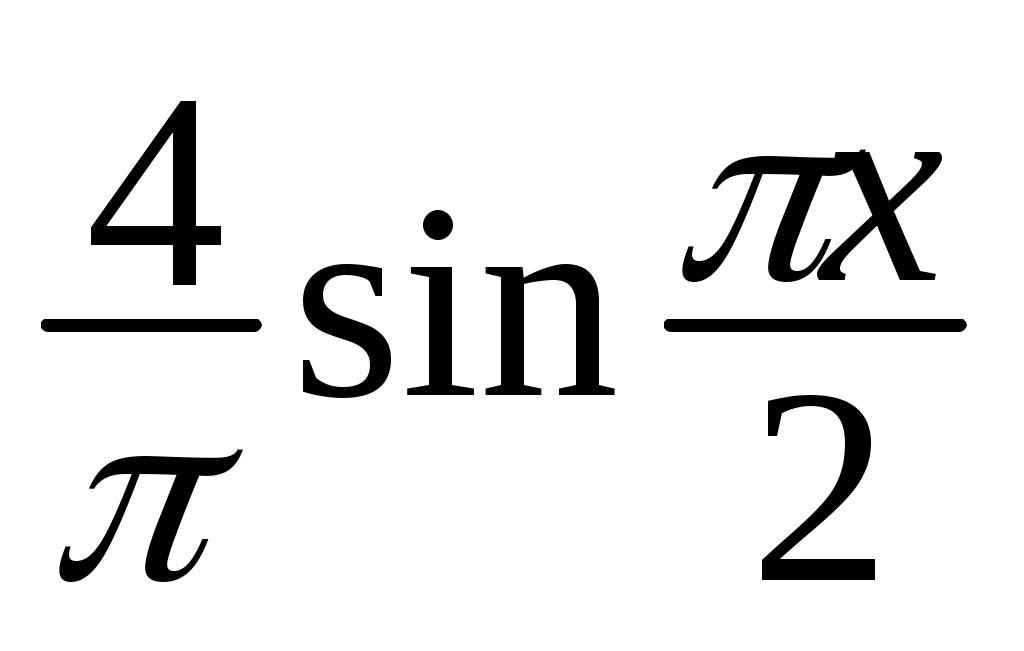 –
– 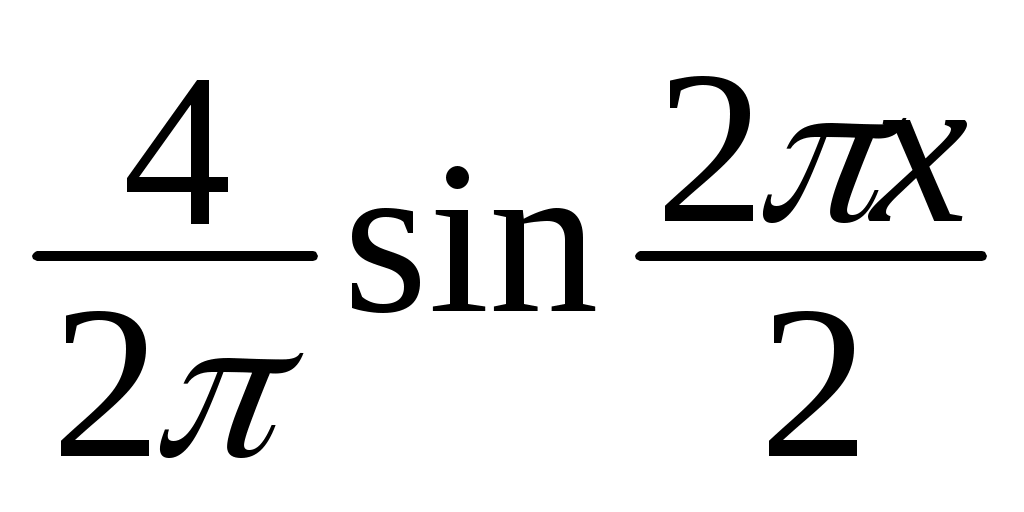 +
+ 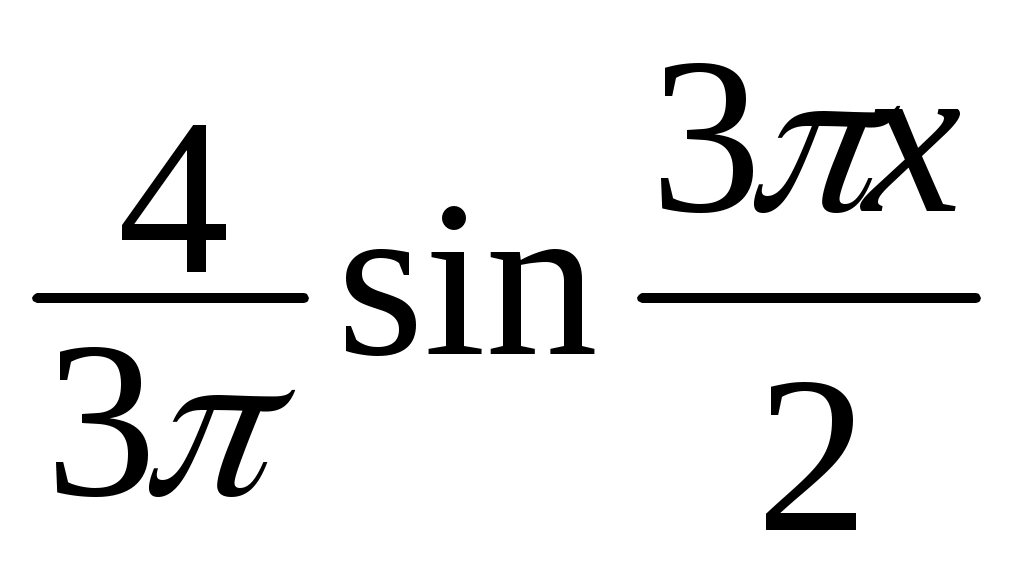 – ... = –
– ... = – 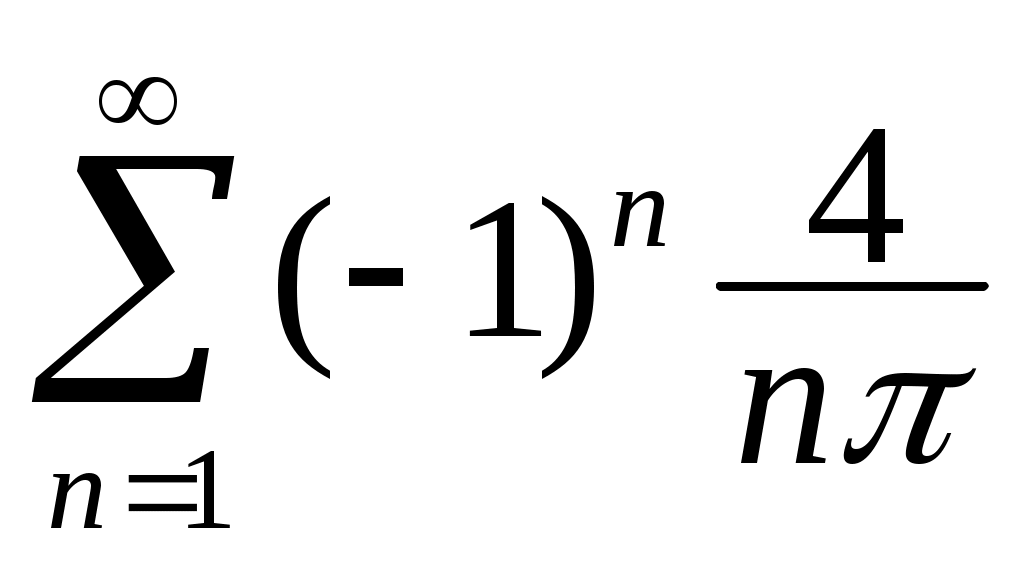 .
.
Пример 6.
Разложить в ряд Фурье функцию f(x) =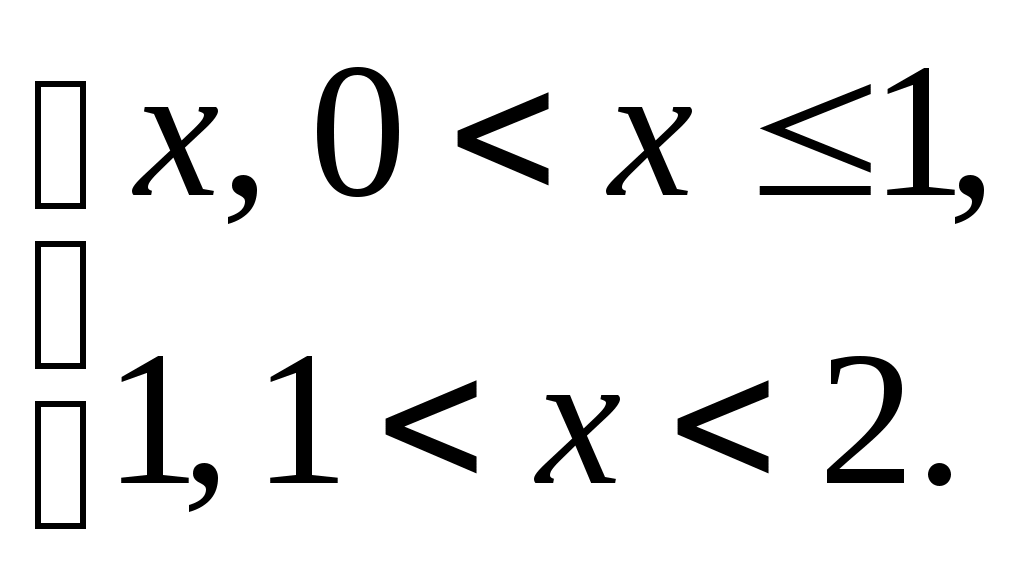
Решение:
Воспользуемся замечанием. Произведем замену переменой х =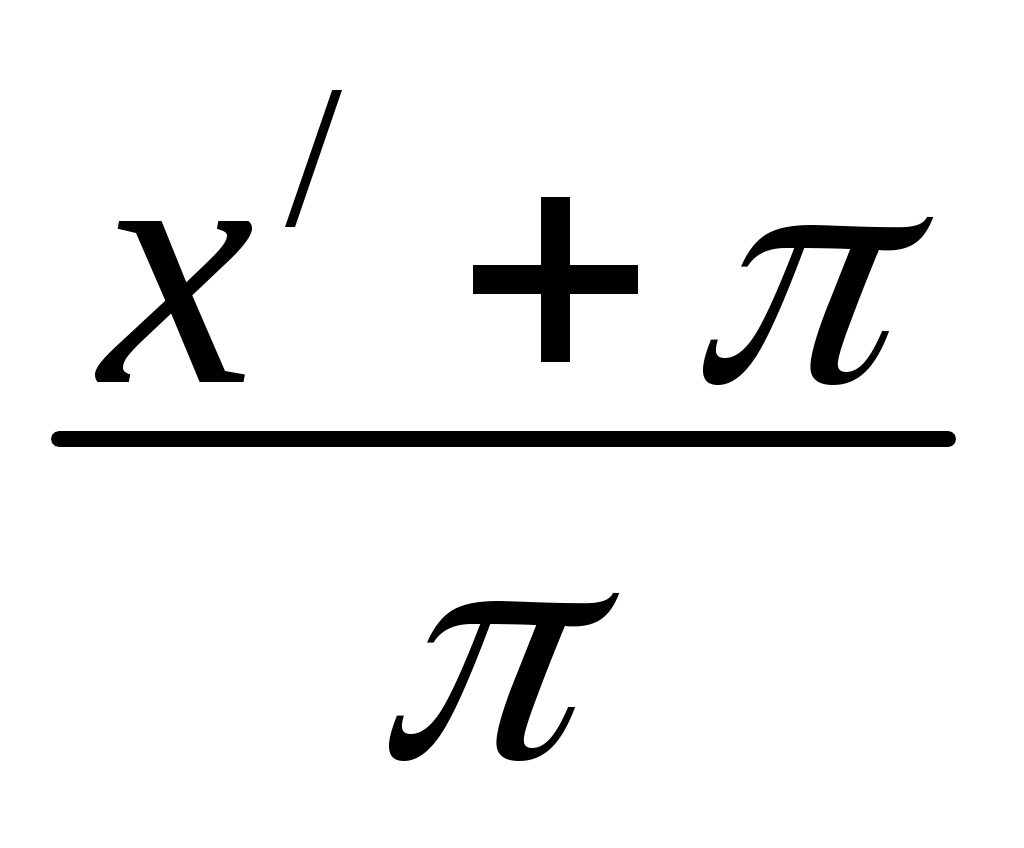 , т.о. получаем функцию:
, т.о. получаем функцию:
f
при 0 < х / < .
при - < х / 0,
(x) =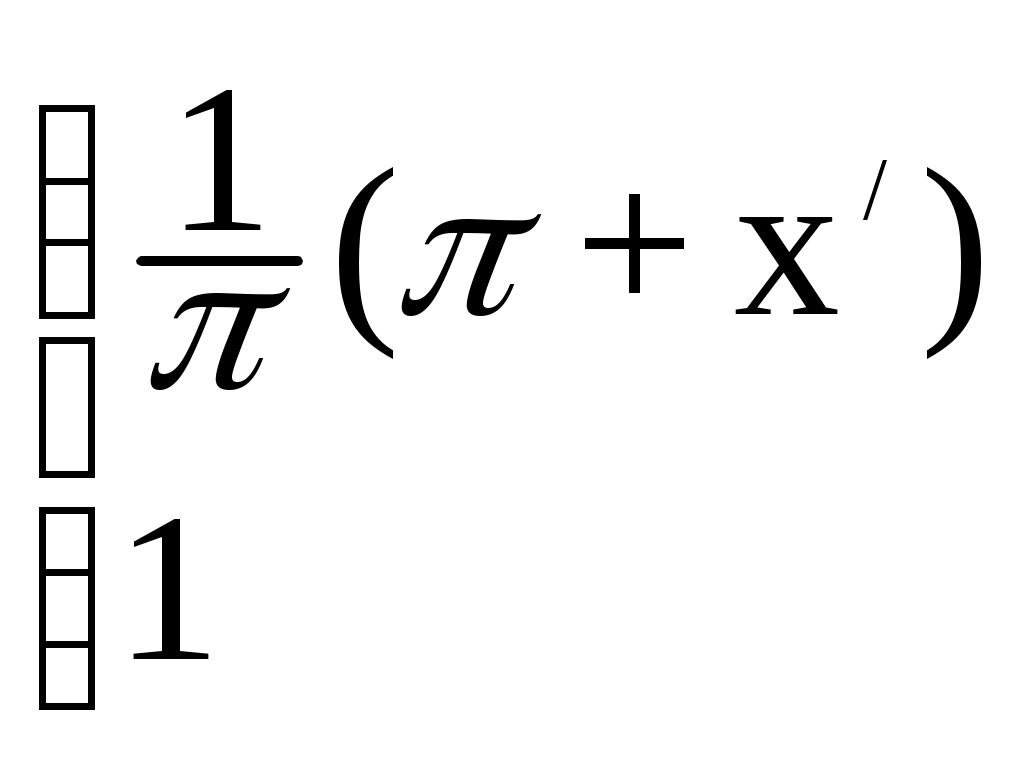
Найдем коэффициенты Фурье.
а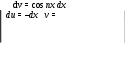 0 =
0 = 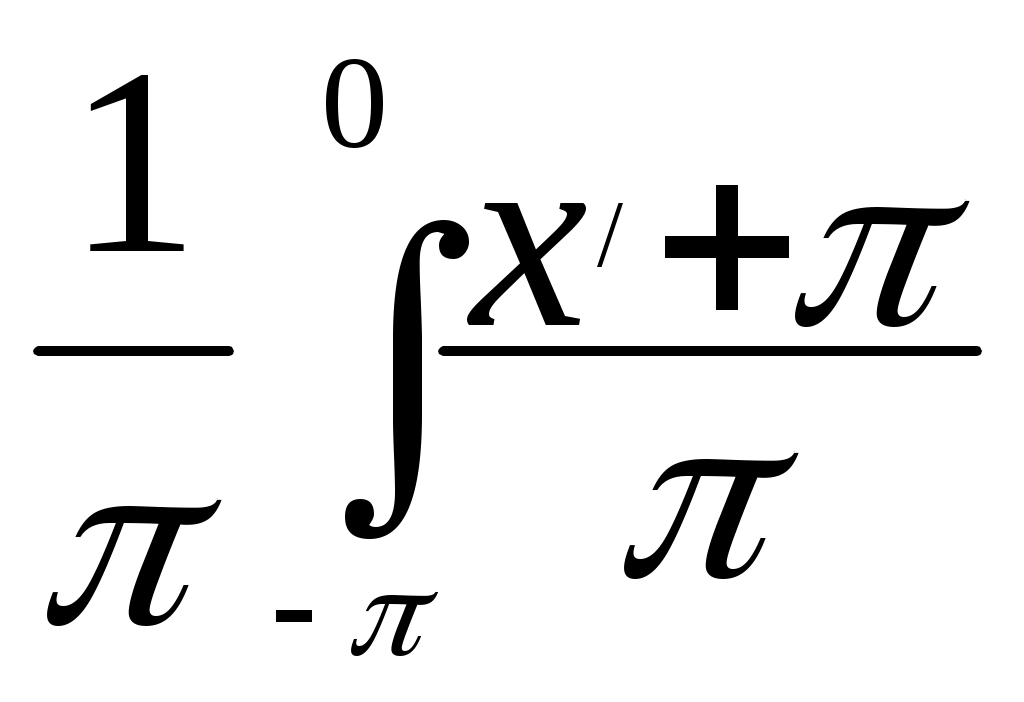 dx / +
dx / + 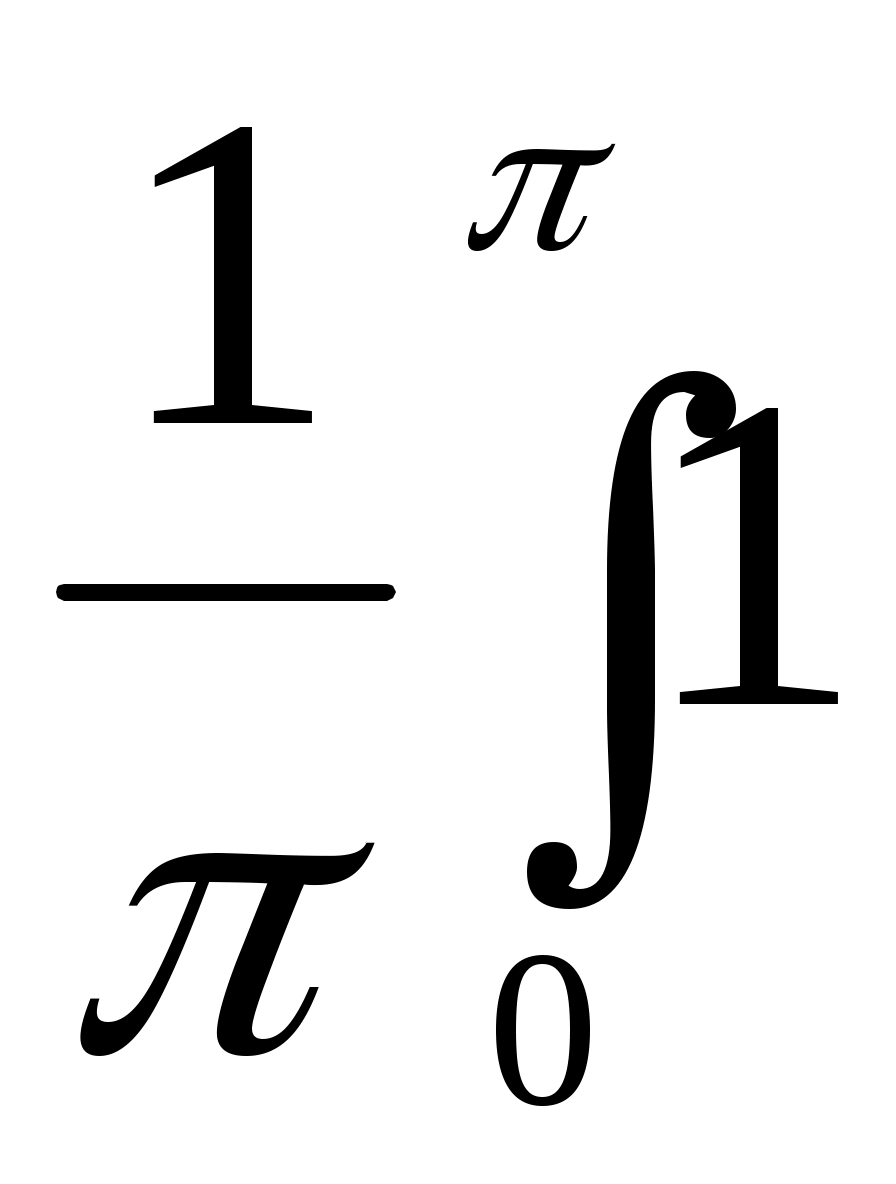 dx / = 3/2.
dx / = 3/2.
an=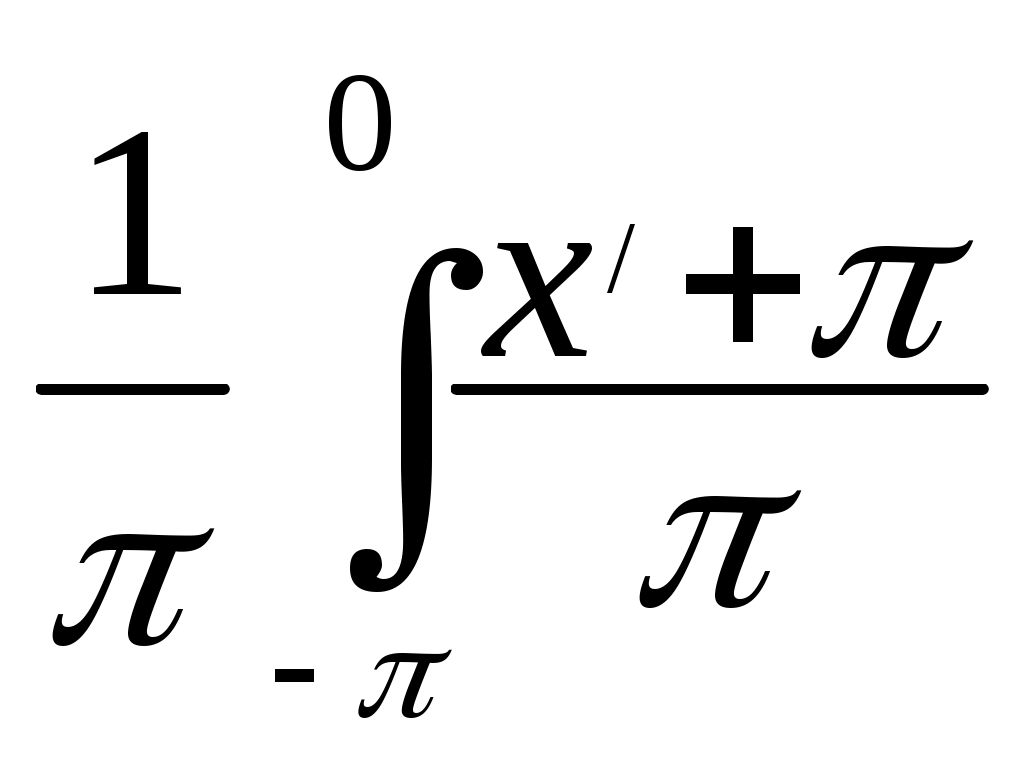
гдеbn=
Пример 2. Разложить в ряд Фурье функцию, определенную равенством f(x) = x при – < x .
Решение:
f
 (x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.)
(x) имеет период 2, удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье. f(–x) = f(x), т.е. она четная. (См. рис. 3.)По формулам (1.17) и (1.18) найдем коэффициенты Фурье:
а0 =
аn =
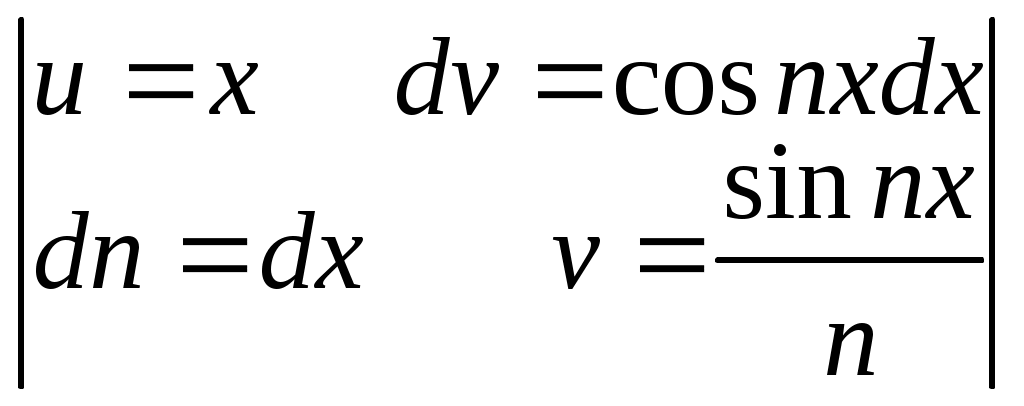 =
==
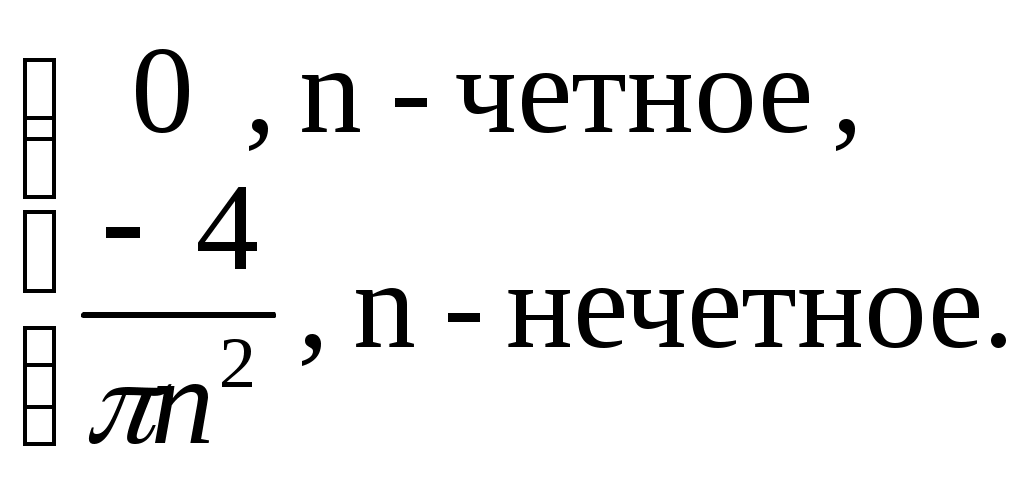
Следовательно, ряд Фурье для данной функции имеет вид:
f(x) =
На интервале [–; ] ряд сходится к функции x .
Пример 3. Разложить в ряд Фурье функцию: f(x)=
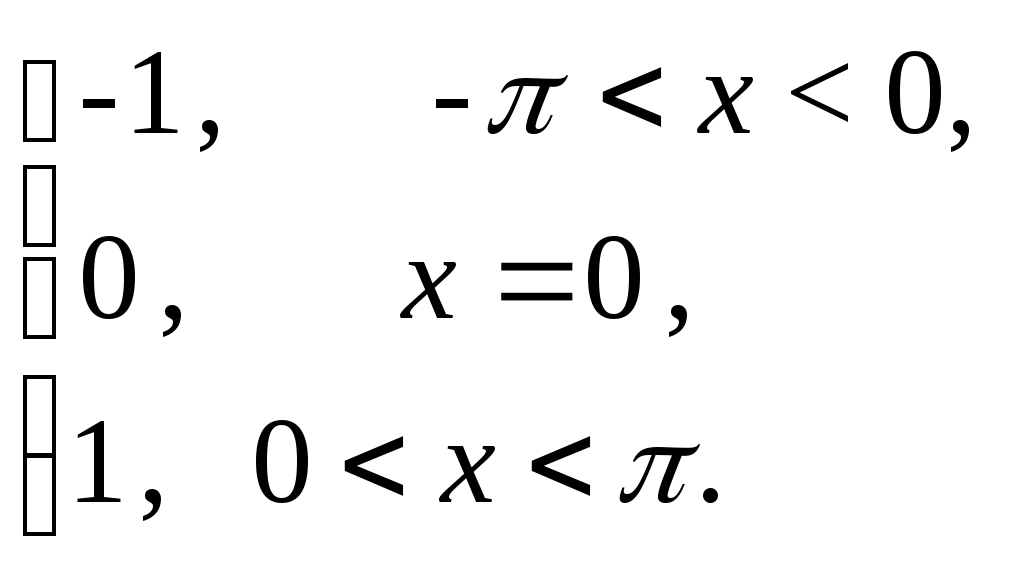
Решение:
f(x) имеет период 2. Она удовлетворяет условиям теоремы, т.е. разлагается в ряд Фурье.
f(–х) = – f(x) (см. рис. 4), т.е. f(x) – нечетна, следовательно а0 = 0 и аn= 0.

Рис. 4.
По формуле (1.21) найдем коэффициент Фурье:
b n =
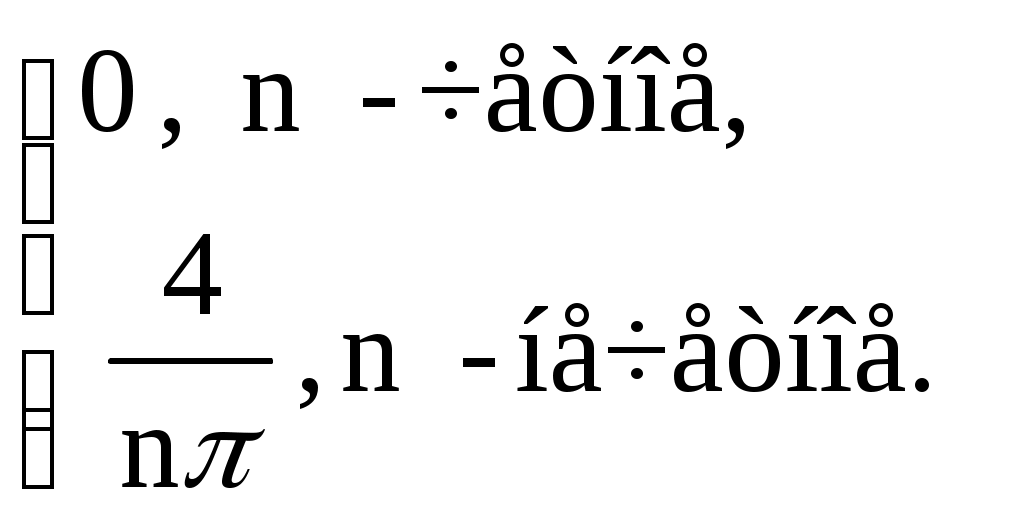
b2k+1 =
Следовательно, ряд Фурье для данной функции имеет вид:
f(x) =
f(x) =
На интервале [–; ] ряд сходится к функции f(x), в точках х = 0 и х = – к нулю.
§ 5. Сдвиг основного промежутка.
Вся теория рядов Фурье излагалась для функций, заданных на отрезке [–; ], однако вместо этого отрезка можно было бы положить в основу рассуждения любой другой отрезок длины 2, так как 2 есть период всех функций системы 1, cos x, sin x, cos 2x, …, и справедлива
Теорема 9. Если функция f(x) имеет период 2, то интеграл
Теорема 10. Если f(x) дифференцируема на отрезке [0; 2], то всюду на открытом промежутке (0, 2) будет
f(x) =
, где
а0 =
аn=
bn=
ряд сходится в точках x= 0, x= 2, где его сумма равна
( без доказательства)
Пример 4. Разложить в ряд Фурье функцию f(x) = x, заданную на отрезке [0; 2].
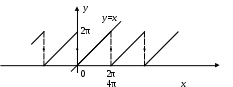
Рис. 5.
Решение:
График функции изобразим на рис. 5. Видно, что функция – разрывная. Найдем коэффициенты Фурье. Здесь
а0 =
аn =
bn =
Стало быть, при 0 < x < 2π будет x =
В точках x= 0 и x= 2 сумма S(x) ряда равна .
§ 6. Разложение в ряд Фурье функций с периодом 2ℓ.
Пусть функция f(x) задана и дифференцируема на отрезке [–l; l]. Положим φ(z) =
Тогда φ(z) будет заданной и дифференцируемой уже на отрезке [–π; π].Значит к φ(z) применима теория, изложенная выше, поэтому при – π < z< π будет
φ(x) =
Положим в этом равенстве
f(x) =
где а0 =
Если f(x) – четная, то
где а0 =
Если f(x) – нечетная, то
где bn=
Замечание. Можно от периода 2
Пример 5. Разложить в ряд Фурье функцию f(x) = x, заданную на интервале –2 х 2.
Решение:

Рис. 6
График функции f(x) =
x изображен на рисунке 6. Видно, что функция нечетная с периодом 2ℓ = 4, то есть ℓ = 2. Найдем коэффициенты Фурье по формуле 1.30.
bn=
= –
=
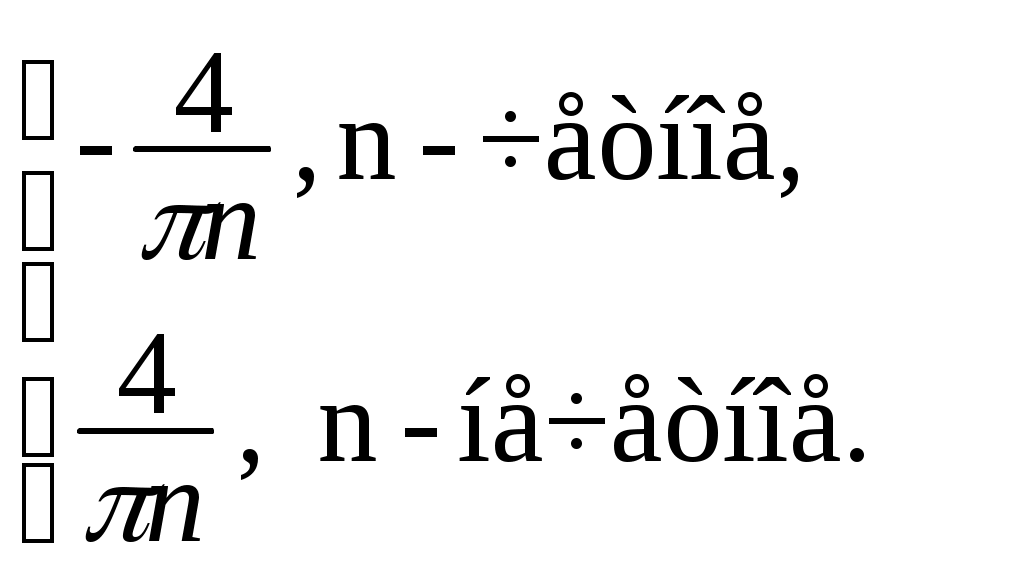
Следовательно, по 1.29 разложение в ряд Фурье функции f(x) имеет вид:
f(x) = x =
Пример 6.
Разложить в ряд Фурье функцию f(x) =
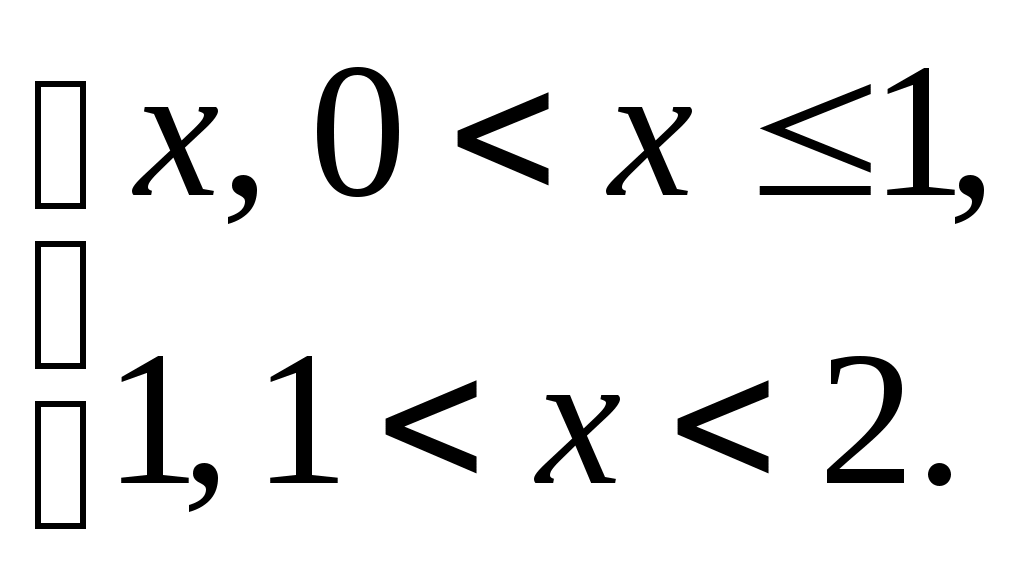
Решение:
Воспользуемся замечанием. Произведем замену переменой х =
f
при 0 < х / < .
при - < х / 0,
(x) =
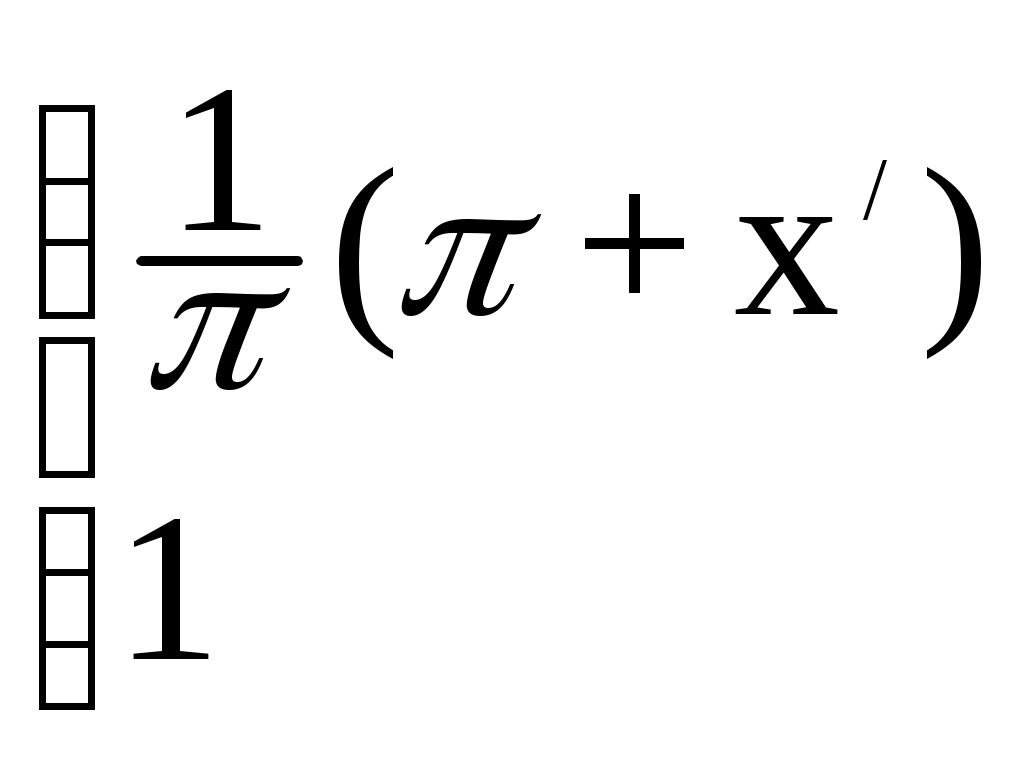
Найдем коэффициенты Фурье.
а
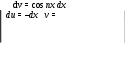 0 =
0 = an=