Файл: Диссертация ылыми жетекшісі п.. к., ауым проф м. а. М. Т. Искакова орауа жіберілді.docx
Добавлен: 12.12.2023
Просмотров: 191
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Логикалық есептердің классификациясы
Логикалық есептерді классификациялау үшін математикадан жақсы дос болумен қатар, олардың көп түрлілігін ескерген жөн. Кейбір логикалық есептер жеңіл бір амалмен шыға салатын болса, енді біреулері алгоритмдік шешу жолын міндетті етеді және көп амалдан тұрады. Оларды классификациялау ретін қойғанда әр маман әр түрлі етіп қоюы мүмкін. Логикалық есептерді классификациялауды елестету үшін бірнеше логикалық есептерді шешіп көрейік. Логикалық есептердің көптүрлілігі оларды шешу жолдарының да көптігін көрсетеді. Айталық, мынандай есеп берілсін: Бөтелкеде, стаканда, құмырада, банкада сүт, лимонад, квас, су бар. Су мен сүт бөтелкеде емес. Лимонад құйылған ыдыс құмыра мен квас құйылған ыдыстың арасында. Банкаға құйылған лимонад та су да емес. Стакан банка мен сүт құйылған ыдыстың қасында. Қандай сұйық қай ыдысқа құйылған. Кем дегенде екі әдіспен шығаруға болады. Логикалық пайымдау арқылы, кесте құру арқылы шығаруға болады.
-
Логикалық пайымдау арқылы шығарсақ.
Логикалық пайымдасақ, бөтелкеде не лимонад, не квас. Банкада не сүт, не квас. Алайда сүт пен банка бір-біріне жақын орналасқандықтан, банкада сүт емес, квас. Сондықтан сүт құмырада.Су болса стаканда, ал лимонад бөтелкеде. Енді кестелік әдіспен шығарып көрсек:
1 – кесте
| | Бөтелке | Стакан | Құмыра | Банка |
| Сүт | - | - | + | - |
| Лимонад | + | - | - | - |
| Квас | - | - | - | + |
| Су | - | + | - | - |
Әр сөйлемді оқыған сайын «–» немесе «+» таңбасын қоя отырып,есептің жауабын табамыз.
Келесі есепте теңдеу құру қажет. Ақдананың ойлаған санынан ең үлкен бір таңбалы санды азайтып, нәтижеге ең кіші екі таңбалы санды қосқанда 100 шықты. Ақдана қандай сан ойлады?
Шешуі: сан – х
(х-9) + 11 =100
х – 9 = 99
х = 108
Жауабы: 108
Келесі есеп адамның жасын есептеуге арналады: Қазір ағасы қарындасынан 5 жас үлкен. 4 жылдан соң, олардың жастарының қосындысы 19 жас болады. Қазір қарындасы неше жаста, ағасы неше жаста?
Шешуі:
Белгілеу енгіземіз:
қарындасы – х
ағасы – х + 5
4 жылдан соң
қарындасы – х + 4
ағасы – х + 5 + 4
(х + 4) + (х + 5 + 4) = 19
х + 4 + х + 9 = 19
2х = 19 – 13
2х = 6
х = 3
Жауабы: Қарындасы – 3 жаста
Ағасы – 8 жаста
Ендігі есептің түрі, артығын алып тастау немесе теңдеу құру арқылы шығаруға болады. Мысалы, Елдостың тауықтары мен қозылары бар. Қозылар тауықтардан 3 есе кем. Қозылар мен тауықтардың барлығында 40 аяқ бар. Елдостың неше қозысы, неше тауығы бар?
Шешуі:
Белгілеу енгіземіз:
Тауық – 3х
Қозы – х
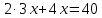
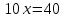
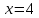
Жауабы: қозы – 4, тауық – 12
Яғни есептерді классификациялау кезінде, ретке келтіру үшін есептерді белгілі-бір типке жатқызып қоямыз. Алайда, бұл оларды шығарудың жалғыз тәсілі емес және оқушыны да әдіс таңдау кезінде шектемеген жөн. Келесі тарауларда әр классификациялау түрімен кеңірек танысып,оларды шығару жолдары көрсетілетін болады. Біздің логикалық есептерді классификациялау реті осындай:
-
Артығын алып тастау; -
Адамның жасына арналған есептер; -
Кестелердің құру арқылы шешілетін есептер; -
Кері жүріс арқылы шығарылатын есептер; -
Жалған тұжырымдары бар есептер; -
Дұрыс пайымдау әдісі.
Логикалық есептерді классификациялау кезінде әр маман әр түрлі әдіс қолданғанымен, барлығында бірдей жеңілден қиынға қарай жылжу алгоритмі сақталған. Мәселен, А.В.Спивактың «Тысяча и одна задача» оқулығын қарасақ, есептерді классқа бөлу реті келесідей:
-
Сіріңкелер; -
Арғы бетке өткізу есептері; -
Қалжың есептер (белгілі бір шығару әдісі жоқ есептер); -
Кесу есептері; -
Жасқа байланысты; -
Қанша алу керек; -
Жарыстар; -
Жұптылық; -
Логика және пайымдау; -
Пайыздарға арналған есептер; -
Дирихле, комбинаторика т.с.с.
Осылайша күрделеніп кетеді. Ал Светлана Степановнаның «Логические задачи и их типы» атты еңбегінде классиффикациялау реті келесідей:
-
Жұмбақтар (есептер типі А.В.Спивактағы қалжың есептерге ұқсас); -
Бұрыннан келе жатқан логикалық есептер; -
Сіріңкелер 2 саты төмен түскен; -
Логика және пайымдау; -
Сөздері бар есептер (А.В.Спивак бұл тарауды көбірек бөлікке бөлген); -
Құю және ауыстырып құю есептері; -
Тізбектер: -
Уақытқа байланысты және т.с.с.
Байқап отырғанымыздай, кей тақырыптар дәл қайталанса, кей тақырыптар бір-бірінде кездеспей екі кітапта бөлек-бөлек кездеседі. Ал кей тақырыптар бір классификацияға біріктіріліп, бір тақырып болып берілген. Енді өзіміздің отандық “Пифагор”- қосымша білім беру орталығында жұмыс істеген кезімде, біз балаларды келесідей классификацияға бөліп оқыттық:
1. Ал, санайық (арифметикалық санаулау көп кездесетін есептер типі);
2.Кері жүріс;
3.Плюс-минус 1;
4.Артығын алып тастау;
5.Жұп-тақтылық;
6.Кесу есептері;
7.Арғы бетке өткізу есептері;
8.Қалжың есептер;
9.Дирихле;
10.Дирихле және т.с.с.
Яғни, отандық еңбектедің бірін алып қарасақ та, жалпы есептер тобы бір шеңбердің ішіндегі есептер, тек берілу реті мен кей тақырыптардың классификациясы өзгерген. Жоғарыда айтып өткеніміздей, кейбір типтегі есептердің екі немесе одан да көп шешімі болғандықтан, оларды әр материал құрастырушы әр түрлі тарауға енгізуі әбден мүмкін, әрі талдау барысында біз оған көз жеткіздік. Бұл еңбектерді талдай отырып, классиффикациялардың түрлерінің көптігіне көз жеткіземіз. Логикалық есептердің классификациясын жүйелеу үшін,жазылған еңбектерде қандай классификациялық тараулар бар екенін санау керек. Нәтижесінде, 31 классификациялық тарау бар екеніне көз жеткіземіз. Оларды келесі түрлерге бөлейік:
А) Оқиғасы бар логикалық есептер : 1) қатынастары бар есептер 2) бірнеше қатынастары бар есептер 3) теңдік қатынасы бар есептер 4) элементтерін салыстыру қолданылатын есептер 5) арғы бетке өткізу есептері 6) жарыстық есептер 7) Сіріңкелері бар есептер 8) қалжыңы бар есептер 9) Қызықты есептер: шеңбер бойымен санау, домино, дойбы, сиқырлы текше жайлы есептер, геометиялық есептер.
В) Әдістемелік шешімі болатын логикалық есептер: 1) айқын бір жауапты көрсететін есептер; 2) қажет емес амал болса да сол амалды орындауға итермелейтін есептер 3) берілген өлшемдермен қандай да бір арифметикалық амалдарды орындауды қажет ететін есептер; 4) есепті кері жүру, яғни жауаптан бастап берілгеніне дейін шығару; 5) жандандыруға арналған есептер; 6) қалдық арқылы бүтін бөлігін табуға арналған есептер; 7) тұжырымдаманың шынайылығын орнатуға арналған есептер; 8) кестелерді қолдану арқылы шығатын есептер; 9) графтардың көмегімен шығатын есептер; 10) мүмкін болатын жауаптырды теру арқылы шығатын есептер; 11) жиындарды реттестіруге арналған есептер
С) Логикалық әдістермен шығатын логикалық есептер: 1) шаблонды ойлаудан арытуға арналған есептер; 2) шешімі талқылау мен пайымдауға негізделген есептер; 3) анализге, синтезге арналған есептер 4) артығын ысырып тастауға арналған есептер; 5) ұқсастыққа арналған есептер; 6) белгілі бір қасиеті арқылы классификациялауға арналған есептер.
Аталған еңбектерді анализдей отырып, есептерге ең өп классификация берген А.В.Спивак екенін байқаймыз.
Ең жиі кездесетін классификациялар: а) матодикалық шешімі барлар; б) мағыналық құрамына байланысты; в) логикалық шешу әдістері арқылы.
Есептерді классификациялау барысында тәжірибелі авторлар методикалық шешу әдістері мен мағынасына қарай классификациялаудың 6 тарауын ерекшелейді:
-
Қатынастарға арналған есептер -
Кестелер құру арқылы шығатын есептер -
Арғы жағына өткізу жайлы есептер -
Графтар арқылы шығатын есептер -
Мүмкін болатын жауаптарды теріп шығу есептері -
Қызықты есептер
Енді біздің берген классифиациямыз келесідей:
-
Артығын алып тастау әдісі; -
Адамның жасына арналған есептер; -
Кесу есептері; -
Кесте құру арқылы есептерді шешу; -
Кері жүріс әдісі; -
Пайыздарға арналған логикалық есептер; -
Жұмысқа арналған есептер; -
Қозғалысқа арналған логикалық есептер; -
Теңдеу құру; -
Жұптылық; -
Сандардың бөлінгіштігі; -
Өлшеулер.
Логикалық есептерді оқушының даму мақсатында көп пайдаланатын кітаптың біріне Л.Г.Петерсонның кітабын айтуға болады. Бұл кітапта 4836 түрлі есептердің 1204 есебі логикалық болып табылады. Есептердің 24,9% пайызын логикалық есептер құрайды. Түсіндірме бөлігі мен есептер құрылымының арқасында оқушыда анализ, синтез, салыстыру, жалпыландыру, классификациялау, жүйелендіру, нақтылау мен дәлелдеу дағдыларының дамуына мүмкіндік бар.
Логикалық есептерді классификациялау үшін сонымен есептерді шығару жолы мен мағынасына қарай бір типтерге бөліп, методикасы мен әдісі бір типтестерді жеке-жеке топтастыру қажет. Классификациялау үшін автор көпеген жұмыстарды талдап, пайымдап, әр логикалық есептің мазмұны мен мағынасы, шығару типіне байланысты бөлу процессі.
1.3 5-6 сынып оқулықтарында кездесетін логикалық есептер
5 – сынып математика оқулығын ашсақ, атап айтқанда “Мектеп” баспасының оқулығын, бұрынғы кітаптарда кездеспеген екі, үш, төрт таңбалы сандардың жазылуы көрсетіледі. Олардың белгіленуі, үстін сызып олимпиада мен сайыстарда кездесетіндей жазу мәнерімен берілген. Алғашқы тақырып 50% астамын логикалық есептер қамтиды. Онымен қоса көлдердің тереңдігі, жер-су аттары мен олардың көлемдері, су қоймаларының сыйымдылығы мен жердің көлемдері секілді шынайы фактілерге сәйкестендірілген есептер құрастырылған. Бұл оқушылардың тек қана есеп шығарып қана қоймай, дүние танымдық процесстерді де қамтиды. Онымен қоса математикалық сауатты болуға икемдейтін нұсқаулықтар бар. Кейінгі 2 тақырыпта логикалық есептер кездеспесе де, төмендегідей логикалық пайымдау процессі болатын сұрақтар бар.
Сонымен қатар, оқушыларға стандартты емес ойлау үшін алдын ала мәліметтер беріліп, сол мәліметтер бойынша есеп құрастыратын логикалық есептер бар. Кітаптағы логикалық есептер мейлінше өмірде кездесетіндей шынайылыққа ұқыпталған. Мысалы, жалқының су ішуін әдеттегідей литрмен емес, см3 өлшемімен берілгені. Оқушы алдымен см3 өлшем бірлігін литрге конвертациялап, кейін қажетті мөлшерді табады. Балада алгоритмдік ойлау қалыптасады. Ең аз дегенде әр тақырыпта 1 логикалық есеп кездеседі. Кейбір тақырыптарға логикалық есептермен қатар бизнеске байланысты шығын не табысты есептеуге арналған есептер кездеседі. Бұл есептер тікелей логикалық болмаса да, логикалық мазмұнды әрі кейбірінің шешілуі үшін логикалық әдістер қолданылады. Кестелер әдісімен шығарылатын есептер де жоқ емес және кейбір есептерінде кесте алдын ала беріліп, оқушыға толтыртқызылады. Екі рет саналған шамалар жайлы логикалық есептер бар. Кітаптан мысал алайық:
Екі илеудің арасы 30 м. Осы екі илеуден бір уақытта 4 м/с жылдамдықпен қарама-қарсы бағытта екі құмырсқа жүгіріп шықты. 30 с кейінгі олардың ара қашықтығы қандай болды?
Шешуі:Әлбетте бұл құмырсқалар бір-бірінің қасынан жүгіріп өтіп, әрмен қарай жүретіні сөзсіз. Әрқайсысы 120 м жүргенде, ортада екеуі де жүгіріп өткен 30 м жол бар, яғни ол жол екі рет есептелген. Сол себепті ол жолдың 30 метрін алып тастайыз. Осылайша есепті пайымдау әдісімен шығаруға болады. Суретпен шығару жолы төмендегідей:
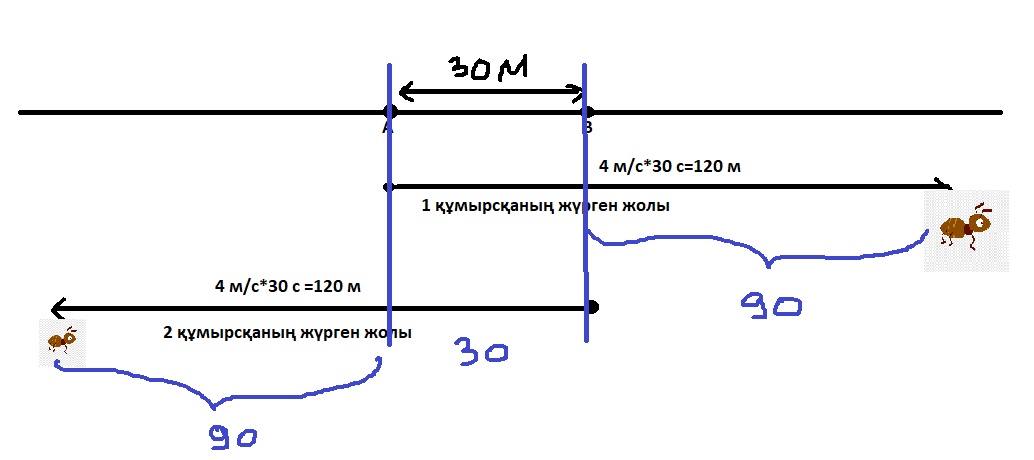
1-сурет
Оларды шығару барысында оқушы тек санап қана қоймай, артық-кем саналған заттарға анализ жасайды. Не болмаса графиктік жолмен кескін жасап үйренеді. Тағы бір логикалық құрылымды есепің түріне кері есеп құрастыруды жатқызу шарт деп ойлаймын. Есепке кері есеп құрастыруды кері жүріс тақырыбына сәйкес етуге келеді.
Сондай ақ көптеген есептер теңдеулер құрастыру әдісімен шығаруға келеді, әрқайсысын бір түрге классификациялап, зерттеу жұмысындағы тақырыптардан алған білімнің көмегімен шығаруға болады. Оқушылар тек қана қосымша білім алып қана қоймай, оны күнделікті оқып жүрген сабақтарында тиімді қолдана алады. Бұдан олар өздігінен және қосымша білім алудың пайдалы әрі тиімді екенін ұға алады. Логикалық есептердің көптеп кездесуі әсіресе мәтінді есептер шығару тарауына сәйкес келеді. Әр түрлі тақырыптарды қамтиды, онымен қоса бизнеске қатысты логикалық әдіспен шығарылатын есептер бар.