Файл: Диссертация ылыми жетекшісі п.. к., ауым проф м. а. М. Т. Искакова орауа жіберілді.docx
Добавлен: 12.12.2023
Просмотров: 196
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ұлттық бірыңғай тестілеудегі “Математикалық сауаттылық“ пәнінде кездесетін тізбекке қатысты кейбір есептер осы сыныптардан бастап кездеседі. Оқушы жоғарғы сыныпқа жеткенше осы типтес есептерге әбден дағдыланып, болашақ емтихан сынақтардан жеңіл өте алады.
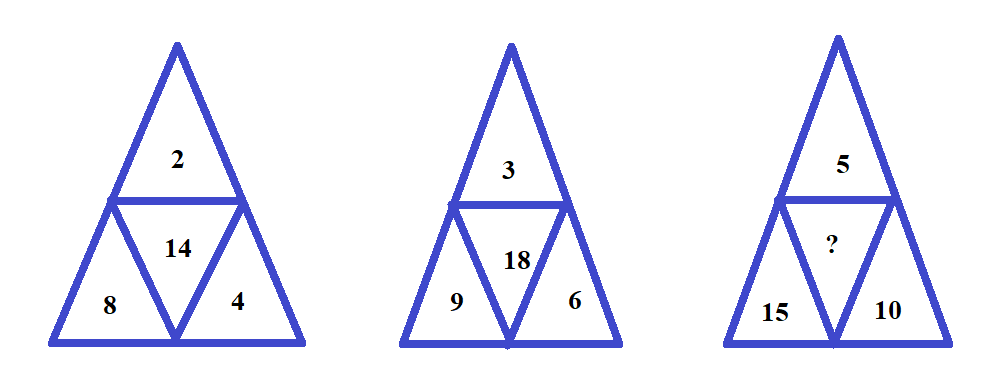
2 – сурет
Натурал сандар тізбегі тарауынан алынған есеп.
Бөлінгіштік тарауында есептерді тек логикалық әдіспен шығарып қана қоймай, белгілі бір топқа тиістілігін дәлелдеу қажет. Дәлелдеу есептері 5 сынып оқушылары үшін ғылыми зерттеу жұмысы секілді, бейне бір проект қорғап шыққандай жеңіс сезімін сыйлап, ғылым мен білімге деген құштарлығын арттырады. Пайымдау әдісін кеңінен қолдануға болады.
Натурал сандарды жәй көбейткіштерге жіктеу тақырыбы осыдан 10 жыл бүрынғы кітаптарда жоқ еді. Логикалық есептерді дәрежемен, арифметикамен байланыстыруда қажетті тақырып. Бұл тақырып жарыстар мен сайыстарда жиі кездесетіндіктен, оқушыларға математикалық білім шеңберін кеңейту процессі жеңілдейді.
Жоғарыда аталып өтілген талдау кітаптың бірінші бөліміндегі логикалық есептерге талдау жұмысы болды. Енді екінші бөлімді талдау барысында бірден байқалатын мәселе, кітаптың 2 бөлімінің 80% жуығы мәтінді есептер және логикалық есептердің пайыздық үлесі әлдеқайда артқан. Есептердің басым бөлігін теңдеу құру арқылы шығаруға болады. Екінші бөлім мәтінді есептерге практика деп айтсақ та болады. Олардың тақырып бойынша көптүрлі болғанымен, шығару жолы бойынша көп классификацияланбаған. Есесіне оқушыларға қол үйретіп, әр тақырыпқа байланысты түрлі логикалық есептерді шығаруға мүміндік бар. Айта кеткенде, бірінші бөлімде алған білімін екінші бөлімде кең қолдану мүмкіндігі бар. Бұл дегеніміз бірінші бөлімде алған білімді пайдаланып, оны шыңдап ары қарай логикалық есептерге көп мән берілуінде. Әлбетте, оқушылардың кейбіріне қосымша білім қажет болады, ал енді бір бөлігі көбірек есеп шығаруға ұмтылады. Екі типтегі оқушыларға да қосымша осы зерттеу жұмысындағы есептер мен тақырыптарды беру оларға ресурс жағынан және негізгі мектептің программасын меңгеру жолында пайдасы тиері сөзсіз.
Дәл сондай 5 сыныптарға арналған “Атамұра” баспасының кітабын қарастырсақ, алғашқы тараулары бұрынғы кітаптарға ұқсасырақ, логикалық пайымдауға сұрақтары көп есептер кездеседі. Логикалық есептер В және С деңгейлерінде көбірек кездеседі. «Мектеп» баспасында кездесетін логикалық есептерден тағы бір айырмашылығы күрделілігі жоғары сайыстық есептерге ұқсас есептер жұлдызшамен берілген. Бұл кітапта логикалық есептердің «Мектеп» баспасында кездесетін логикалық есептерден тағы бір айырмашылығы, «Мектеп» баспасында бизнеске қатысты логикалық есептер берілсе, «Атамұра» баспасында шығармашылық есептер болып беріліп тұр. Логикалық есептерді сурет түрінде беру кеңінен қолданылады, әрі бірнеше пунктіден тұратын логикалық есептер көптеп кездеседі. Кесте арқылы шығарылатын есептер де бар, және олар бірнеше тарауда кездеседі. Демек, оқушы уақыт өте келе шығарған күрделі есептерге типтес есепті тағы да шығарып көруге мүмкіндік алады. Бұл оның есте сақтау қабілетін арттырып, бұрынғы өткен материалды уақытара қайталап отырудың жөн екендігін көреді. Кей тарауларда кестемен шығатын есептер шығармашылық есеп болып берілген. Мысалыға келесі есеп: Стадионнан келе жатқан Қайрат, Мирас, Нүртас және Айдос – футболистер. Қайрат, Мирас және Нұртастың біреуі - қақпашы. Нұртас қақпашы емес. Стадионнан келе жатқан футболистердің қайсысы қақпашы?
2 – кесте
| Футболшы | қақпашы |
| Қайрат | - |
| Мирас | + |
| Нүртас | - |
| Айдос | - |
Яғни, біздің зерттеу жұмысында да осы тақырып аясында шығару жолдары көрсетіліп, есептерге талдау жасалғаннан кейін, оқушыларға өзіндік жұмысқа материал беріледі. Логикалық есептердің кездесетін тағы бір түрі, таразымен өлшеу есептері.
Келесідей түрде берілген есепті талдайық:
Сырт пішіндері бірдей 8 сақинаның біреуі өзгеоерінен жеңіл. Гір тастаы жоқ табақшалы таразымен кем дегенде неше рет өлшеп, жеңіл сақинаны табуға болады?
Алдымен тастарды 3, 3 және 2 тас қылып бөліп алайық. Таразыға 3 тас пен 3 тасты қоямыз. Екі жақтың бірі міндетті түрде еңіл болады, сол жеңіл жағын 1 тастан таразының екі жағына қойып, жеңіл сақинаны табамыз. Екі жақ тең болған жағдайда, үшінші бөлікте тек екі тас қана,соларды таразымен өлшеп, салыстырып аламыз. Бұл тақырып олимпиада мен жарыстарда жиі кездеседі әрі шығару әдісі кең ауқымды болғандықтан, балалардың логикалық дамуына үлкен септігін тигізеді.
Кітапта кездесетін әрі біздің зерттеу жұмысымызда қарастырылатын тағы бір есептің түрі – бастар мен аяқтарды санау. Нөмірі 282 есепке көз жүгіртсек:
Аулада қояндар мен тауықтар жайылып жүр. Тауықтардың қояндардан 8-і артық. Олардың барлығы 46 аяғы бар. Аулада неше қоян, неше тауық жайылып жүр?
Осы типтес есептердің шығару әдісінің бірнеше нұсқасын келесі тарауда көрсететін боламыз. Ең көп кездесетін логикалық есептердің түрін, теңдеу құру арқылы шығатын логиалық есептерге классификациялаймыз. Тағы бір жиі кездесетін логикалық есептің түрі-құю, құмсағатпен белгілі бір уақыт мөлшерін алу секілді есептер. Логикалық есептердің берілуі мен жиілігінде өзгерістер бар. Таразының көмегімен шығатын есептер тарауларда жиі-жиі көптеп кездеседі. Олардың шығарылу әдістемесі көрсетілмеген, алайда белгілі бір алгоритм бойынша шығарып үйренген оқушыға мұндай есептерді шешу қиындыққа соқпайды.
2 5-6 СЫНЫПТАРДА МАТЕМАТИКАНЫ ОҚЫТУДА ЛОГИКАЛЫҚ ЕСЕПТЕРДІ ШЕШУ ӘДІСТЕМЕСІ
2.1 5-сынып оқушыларына логикалық есептерді шешуге үйрету әдістемесі
Артығын алып тастау әдісі
Көптеген дидактикалық материалдарда бұл әдісті Прокруст әдісі деп те атайды.Артығын алып тастау немесе жетпегенін қосып шығару-табылған ақыл.
Қарапайым мысалдан бастайық.
Мысал 1.
Екі сөреде барлығы 10 кітап бар және екінші сөреде 2 кітап артық.Әр сөреде неше кітап бар [5]?
Кең қолданылған әдіс,теңдеулер жүйесін құру.1 сөредегі кітаптар санын «х»,ал екінші сөредегі кітаптар санын «у» деп алайық.Сонда «x+y=10» және
«y-x=2». Жүйені шеше отырып y=6 және x=4 екендігін анықтаймыз.Алайда 5 сыныптарда теңдеулер жүйесін тек олимпиадаға қатысып жүрген немесе арнайы дайындығы бар оқушылар ғана біледі.Сол үшін келесі әдісті қолданайық:
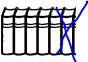
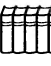
3 – сурет
Қай сөреде қанша екендігін білмегендіктен,артық кітаптарды сызып тастайық,сонда 2 сөреде де 4 кітаптан қалады. Яғни екі артық кітап болмаса әрқайсысында төрт төрттен кітап бар. Осыдан екінші сөреде 6 кітап,бірінші сөреде 4 кітап екендігі белгілі болады. Толық түсінікті болуы үшін тағы бір мысал келтірейік.
Мысал 2.
Аулада қойлар мен тауықтар жүр. Ақжол оның аяқтарын санап еді 20 болды. Айбол олардың бастарын санағанда 7 болды. Аулада қанша қой, қанша тауық жүр?
Шешуі: Есептің шешуін алдымен теңдеу арқылы, кейін жоғарыда көрсетілген әдіс бойынша шығарайық.
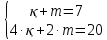Себебі бастарын санасақ 7, аяқтарын санасақ 20. Осы жүйені шешсек 3 қой, 4 тауық екенін анықтаймыз. Енді артығын алып тастау әдісін қолданайық.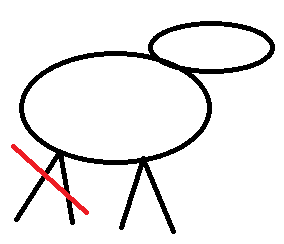
4 – сурет
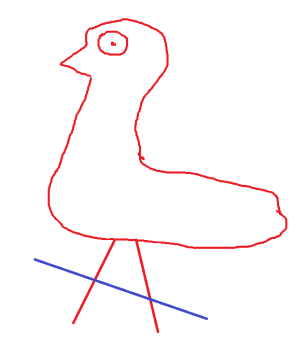
5 – сурет
Егер барлық жануардан екі-екі аяқтан кесіп тастасақ,онда тауықтарда аяқ қалмайды, ал қойларда екі-екіден аяқ қалады. Яғни 7 жануардан 14 аяқ кесілді.Бастапқыда барлығы 20 аяқ санағандықтан, қалғаны 6 аяқ. Демек, қойларда екі аяқтан қалғандықтан, бізде үш қой бар.Тауықтар саны 4.
Тексеру:
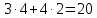
Мысал 3
Екі санның қосындысы 30 тең. Олардың біреуі екіншісінен 6-ға артық. Осы сандарды тап.
Шешуі: Егер артық алтауын алып тастасақ,бұл сандар теңеседі. Яғни 24:2=12. Сандардың біреуі 12. Екіншісі 18. Теңдеу құру арқылы да шығарса болады. Келесі есептерді оқушыларға өз еркінше шығаруға ұсынамын.
А тобы
1.Бір фермерде қозылар және тауықтар бар. Бір күні ол баласын қозы, таукықтарды санауға жіберді. Баласы жануарларды бөлек санамай, жалпы бастарын және аяқтарын санады. 112 аяқ және 46 бас шықты. Фермерде неше қозы және неше тауық бар?
2.Торда қояндар және балапандар отыр. Олардың барлығында 10 бас, 24 аяқ. Торда неше қоян және балапан бар?
3.Патшада қозылар және жалғыз мүйізді бұқалар бар. Оларда барлығы 16 аяқ және 5 мүйіз бар. Патша сарайында жалғыз мүйізді бұқалар саны нешеу [6]?
4.Бірнеше гномдар өздерінің пониларына жүк артып, алыс сапарға аттанды. Оларды троллдар байқап қалып, көшпенділердің 36 аяқ және 15 бас болғанын санады. Гномдардың және понилардың санын тап?
Банкада қоңыздар және өрмекшілер бар, оларда барлығы 10 дене және 68 аяқ бар. Әр қоңызда 6 аяқ бар. Әр өрмекшіде 8 аяқ бар. Банкадағы өрмекшілер мен қоңыздар санын анықтаңыз?
5.10 велосипедистте 27 дөңгелек бар. Велосипедтер 2 дөңгелекті және 3 дөңгелекті. Төрт дөңгелекті велосипед жоқ. Неше велосипедшінің дөңгелегінің саны үшеу, нешеуінікі екеу?
В тобы
6.Дүкеннің жанында көліктер және екі дөңгелекті велосипедтер тұр. Олардың барлығы 10, ал дөңгелектердің саны 30. Қанша велосипед және қанша көлік тұр?
7. Тұрақта 10 автокөлік бар: жеңіл көліктер және жүк авто көліктер. Жеңіл автокөліктерде 4 дөңгелек, ал жүк автокөліктерде 6 дөңгелек бар. Барлығы 46 дөңгелек. Тұрақта неше жүк және неше жеңіл автокөлік бар?
8.Инкубаторда 20 жұмыртқа жатты. Кейбіреулерінен қаздар, ал қалғандарынан қолтырауындар шықты. Барлығының аяғы 54 болды. Жұмыртқаны жарып шыққан қолтырауындардың және қаздардың санын тап?
9.Хайуанда 2 оң аяғы, 2 сол жақ аяғы, 2 артқы аяғы және 2 алдыңғы аяғы бар. Хайуанда барлығы қанша аяқ бар [1]?
10.Көк шалғында қырықаяқтар және үшбасты айдаһарлар жайылып жүр. Оларда барлығы 20 бас және 110 аяқ бар. Үшбасты айдаһардың неше аяғы бар?
С тобы
11.11 велосипедшіде 31 дөңгелек бар. Төртдөңгелекті велосипед біреу. Неше екідөңгелекті және үшдөңгелекті велосипед бар?
12.Қорапта өрмекшілер және қоңыздар бар. Қорапта барлығы 6 бас бар, ал аяқтардың саны 42 . Қоңыздардың және өрмекшілердің санын табыңыз?
13.Бөлмеде төртаяқты орындық және үшаяқты табуретка бар. Егерп барлық орындықтарда және табуреткаларда адамдар отырса, бөлмеде 39 аяқ болады. Бөлмеде неше табуретка және неше орындық бар?
14.Мысықтың табанында 5 тырнақ бар, ал балапанда 4-еу. Аулада 10 мысық және балалапандар жүр, барлығының тырнақтарының саны 104. Аулада барлығы неше мысық бар?
15.Саваннада керіктер және түйеқұстар жүгіріп жүр. Оларда барлығы 14 көз және 20 аяқ. Түйеқұстардың және керіктердің саны нешеу? Қайсысы көп [2]?
*Қай әдіспен шығару оқушының өз еркіне тиесілі. Белгілі бір әдіске шегелеп қою оқушының ой өрісін шектейді.
Адамның жасына арналған есептер
Мысал 1. Ермек 12 жаста,ал оның ұстазы 42 жаста.Қанша жылдан кейін ұстазы Ермектен 2 есе үлкен болады?
Шешуі:
1 тәсіл. Ермекке қанша жыл өтсе,ұстазына да сонша жыл өтеді.Яғни белгілі быр жыл өтіп,екіге көбейтсек ұстаздың жасы шығуы тиіс.
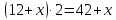
Теңдеуді шеше отырып х=18 екенін анықтаймыз.
2 тәсіл: Қазір екеуінің жас айырмашылығы 30,ал егер олардың жас айырымынан кішісінің жасын алсақ,қанша уақыттан кейін олардың жас айырымы 2 есе болатынын көрсетеді.Себебі кішісінің жасын екі рет азайтқандықтан кішісінің жасы екі рет қолданылды.
42-12=30,
30-12=18
А тобы
1.Ұлы 7 жаста, әкесі 31 жаста. Неше жылдан соң әкесінің жасы ұлының жасынан 2 есе артық болады?
2. Атасы 56 жаста, ал немересі 14 жаста. Неше жылдан кейін атасының жасы немересінің жасынан 2 есе артық болады?
3. Атасы 58 жаста, оның баласы 32 жаста, немерелері 11 жаста және 7 жаста, Неше жылдан кейін атасының жасы баласы мен немерелерінің жастарының қосындысына тең болады?
4. Шешесі 42 жасқа келгенде , үлкен қызы 19, ортаншы қызы 11, кенжесі 2 жасқа толады. Қанша уақыттан кейін шешесінің жасы үш қызының жасының қосындысына тең болады?
5. Қазір анасы 54 жаста. Ұлы 20-да, қызы 6-да. Неше жылдан кейін ұлы мен қызының жастарының қосындысы анасының жасына тең болады?