Файл: Практическая работа 2 Определение показателей безотказности невосстанавливаемых объектов по статистическим данным.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 142

Скачиваний: 7

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическая работа № 2

«Определение показателей безотказности

невосстанавливаемых объектов

по статистическим данным»

Цель работы:

  1. Закрепить теоретические знания, полученные в разделе «Единичные показатели надежности» по вопросу «Показатели безотказности».

  2. Освоить методику определения показателей безотказности по статистическим данным о надежности неремонтируемых изделий на определенном промежутке времени.

  3. Получить практические навыки построения и анализа зависимостей показателей безотказности во времени



  1. МЕТОДИКА определения показателей безотказности на определенном промежутке времени

На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.

Показатели безотказности определяются для каждого интервала в следующей последовательности:

  1. Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле

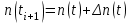(2.1)

  1. Определяем количество работоспособных изделий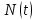 на конец каждого периода по формуле

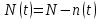, (2.2)

где n(t) – количество отказавших изделий на конец рассматриваемого периода за период от 0 до t.

  1. Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле

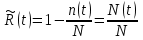. (2.3)

  1. Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле

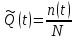. (2.4)

  1. Определяем статистическую оценку плотности вероятности отказов по формуле

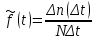
, (2.5)

где Δn(Δt) – количество отказавших изделий в данном временном интервале Δt.

  1. Определяем значение интенсивности отказов по формуле

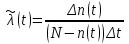, (2.6)

  1. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

  1. Изучить методику расчёта показателей безотказности за определенный промежуток времени

  2. Проанализировать условия задачи и определить исходные данные для расчета показателей безотказности

  3. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.

  4. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

  5. Результаты расчета отразить на графиках.

  6. Ответить на контрольные вопросы.



  1. Оформление результатов работы

Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 1000 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 2.1.

Задание:

1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.

2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

3. Результаты расчета отразить на графиках.

Решение.

  1. Согласно условию задачи длина рассматриваемых периодов Δt равна 100 часам

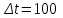час.

  1. В начальный период времени изделия должны находиться в работоспособном состоянии и количество отказавших изделий на время t=0 равно 0, следовательно

.

.

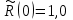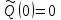  1. Определяем количество работоспособных изделий на конец первого периода по формуле (2.2)

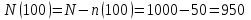
шт.

  1. Определяем статистическую оценку вероятности безотказной работы на конец каждого периода по формуле (2.3)

.

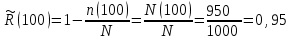  1. Определяем количество отказавших деталей нарастающим итогом на конец первого периода по формуле (2.1)



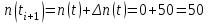
  1. Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле (2.4)

.

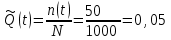  1. Определяем статистическую оценку плотности вероятности отказов по формуле (2.5)

.

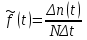  1. Определяем значение интенсивности отказов по формуле (2.6)



  1. Аналогично проводим расчеты для всех остальных периодов и результаты расчета для удобства сводим в таблицу 2.1

Таблица 2.1 – Результаты расчета статистических оценок показателей безотказности

Временной интервал Δt, час
Количество отказов за данный интервал Δn(t)
Количество работоспособных изделий на конец периода N(t)
Количество отказавших изделий на конец периода

n(t)
Вероятность безотказной работы R(t)
Вероятность отказа Q(t)
Плотность вероятности отказов f(t),

·10-2
Интенсивность отказов λ(t), ·10-2







2406















0 – 100

36
2370
36
0,985
0,015
0,00015
0,00015190

100 – 200

45
2325
81
0,966
0,034
0,00019
0,00019355

200 – 300

90
2235
171
0,929
0,071
0,00037
0,00040269

300 – 400

590
1645
761
0,684
0,316
0,00245
0,00368663

400 – 500

339
1306
1100
0,543
0,457
0,00141
0,00259571

500 – 600

392
914
1492
0,380
0,620
0,00163
0,00428884

600 – 700

396
518
1888
0,215
0,785
0,00165
0,00764479

700 – 800

90
428
1978
0,178
0,822
0,00037
0,00210280

800 – 900

92
336
2070
0,140
0,860
0,00038
0,00273810

900 – 1000

55
281
2125
0,117
0,883
0,00023
 0,00195730



  1. По данным расчета строим графики зависимости расчетных величин по времени (рисунки 2.1, 2.2, 2.3)

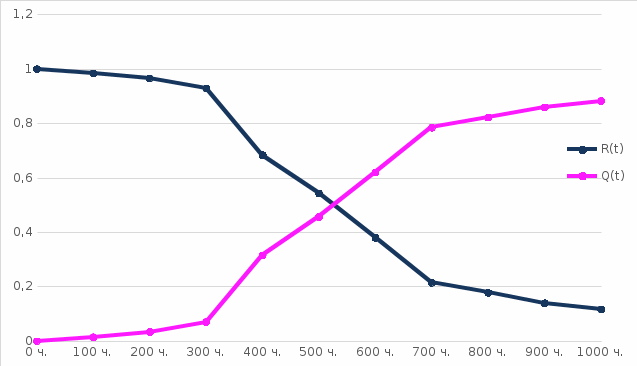Рисунок 2.1 – График зависимости вероятности безотказной работы и вероятности отказа от времени

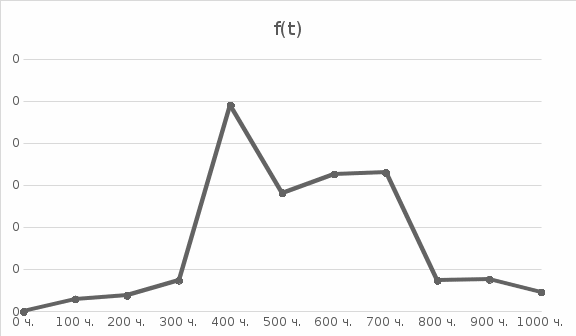Время, t


Интенсивность отказов
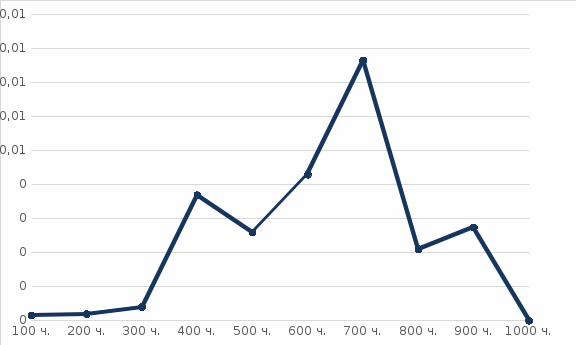Рисунок 2.2 – График зависимости плотности распределения отказов во времени



Рисунок 2.3 – График зависимости интенсивности отказов от времени



  1. Задания для самостоятельной работы

Исходные данные: На испытание поставлено N изделий. Испытания проводятся в течение 1000 часов. Результаты испытаний представлены в таблице 2.2.

Задание:

1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы R(t) во времени.

2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

3. Результаты расчета отразить на графиках.
Таблица 2.2 – Исходные данные для выполнения домашнего задания по практической работе № 2

Номер варианта
Общее кол-во изделий
Количество отказавших изделий за интервал времени ti, шт.

0 – 100

100 – 200

200 – 300

300 – 400

400 – 500

500 – 600

600 – 700

700 – 800

800 – 900

900 – 1000

1
3007
49
99
88
554
594
542
580
86
87
40

2
2379
68
41
37
434
501
282
471
74
77
99

3
2754
75
97
65
554
305
410
407
83
96
82

4
2415
67
56
81
346
405
442
490
57
35
60

5
2785
51
89
98
383
497
575
501
35
92
60

6
2303
63
73
94
263
261
493
484
52
64
87

7
2430
44
62
44
299
482
362
436
49
84
68

8
2337
99
44
75
299
575
411
217
36
46
55

9
2217
66
43
57
395
218
355
510
67
90
58

10
1940
61
66
71
232
376
226
305
72
37
81

11
1913
60
50
100
259
363
438
250
58
58
73

12
2511
72
84
100
377
533
374
520
75
52
44

13
2460
40
94
40
363
426
541
435
86
83
47

14
2306
35
80
37
318
575
387
493
54
35
37

15
1919
37
35
80
340
374
403
215
77
58
96

16
2406
36
45
90
590
339
392
396
90
92
55

17
2654
47
68
77
326
584
470
570
62
74
70

18
2581
83
52
93
431
303
567
345
93
81
89

19
2554
51
48
58
432
218
595
353
99
89
63

20
2626
65
99
73
591
220
550
544
47
60
88




  1. Контрольные вопросы:

  1. Свойства функции вероятности безотказной работы?

  2. Свойства функции вероятности отказа?

  3. Каким образом определяется плотность распределения наработки во времени?

  4. Кривая зависимости интенсивности отказа во времени.

  5. Кривая плотности распределения отказов во времени.

Ответы:

1. Функция вероятности безотказной работы имеет следующие свойства:

- P(0) = 1, то есть вероятность отсутствия отказов в начальный момент времени равна 1.

- 0 ≤ P(t) ≤ 1 для любого t, то есть вероятность безотказной работы всегда находится в диапазоне от 0 до 1.

- P(t) убывает при увеличении времени, что означает, что вероятность безотказной работы уменьшается с течением времени.

- P(∞) = lim P(t) = 0, то есть вероятность безотказной работы стремится к 0 при бесконечном времени работы системы.

2. Функция вероятности отказа имеет следующие свойства:

- Q(0) = 0, то есть вероятность отказа в начальный момент времени равна 0.

- 0 ≤ Q(t) ≤ 1 для любого t, то есть вероятность отказа всегда находится в диапазоне от 0 до 1.

- Q(t) возрастает при увеличении времени, что означает, что вероятность отказа увеличивается с течением времени.

- Q(∞) = lim Q(t) = 1, то есть вероятность отказа стремится к 1 при бесконечном времени работы системы.

3. Плотность распределения наработки во времени определяется как отношение вероятности отказа в момент времени t к интенсивности отказов в момент времени t: f(t) = Q(t) / λ(t). Таким образом, плотность распределения наработки во времени описывает вероятность возникновения отказа в определенный момент времени при заданной скорости отказов.

4. Кривая зависимости интенсивности отказа во времени может иметь различные формы в зависимости от типа системы и ее эксплуатационных условий. Одним из часто встречающихся видов кривой является кривая "модели износа", которая представляет собой увеличивающуюся во времени кривую, отражающую рост интенсивности отказов с увеличением наработки системы.

5. Кривая плотности распределения отказов во времени также может иметь различные формы в зависимости от типа системы и ее эксплуатационных условий. Одним из часто встречающихся видов кривой является кривая "экспоненциального распределения", которая представляет собой убывающую во времени кривую плотности распределения, отражающую вероятность отказа в последующий момент времени при заданной вероятности отказа в текущий момент времени.

Смотрите также файлы