Файл: Организация и управление производством.docx

Пусть, например, мы рассматриваем зависимость величины Y от величины x – y(x).

Невозможность выявления строгой связи между двумя переменными объясняется тем, что значение зависимой переменной Y определяется не только значением переменной x, но и другими (неконтролируемыми или неучтенными) факторами, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.

Вследствие этого корреляционный анализ широко используется при установлении взаимосвязи экономических показателей.

Итак, если с увеличением x значение зависимой переменной Y в среднем увеличивается, такая зависимость называется прямой, или положительной.

Если среднее значение Y при увеличении x уменьшается, имеет место отрицательная, или обратная корреляция.

Если с изменением x значения Y в среднем не изменяются, то говорят, что корреляция нулевая.

Часто при исследовании взаимосвязи между какими-либо показателями представляют изучаемый объект в виде так называемого «черного (кибернетического) ящика».

Самый простой случай – изучение связи между одной переменной x, которую называют фактором (входной переменной, независимой переменной), и переменной Y, которую называют откликом (реакцией, зависимой переменной), рис. 4.

Рис. 4. Представление исследуемой системы в виде «черного ящика»

(один фактор, один отклик)

В более общем случае итогом функционирования системы является целый набор результирующих величин Y_s

. При этом значения откликов Y_s определяются, с одной стороны, совокупностью факторов x_j

, а с другой – набором возмущений (случайных, неконтролируемых факторов x_вi

, рис. 5.

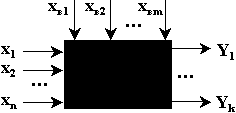
Рис. 5. Представление исследуемой системы в виде «черного ящика»

(общий случай)

Собственно говоря, на протяжении столетий ученые (особенно естествоиспытатели) используют подобные приемы, т.е. наблюдают, что произойдет с явлением, процессом (с откликом Y), если изменять значения влияющих на процесс факторов (переменных x).

Корреляционным полем называется множество точек {X_i, Y_i} на плоскости XY (рис. 6 и 7).

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет положительный угол наклона (/), то имеет место положительная корреляция (см. рис. 6).

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет отрицательный угол наклона (\), то имеет место отрицательная корреляция (см. рис. 7).

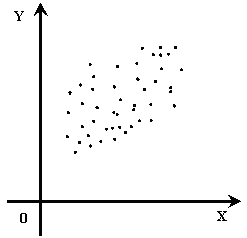
Рис. 6. Пример корреляционного поля (положительная корреляция)

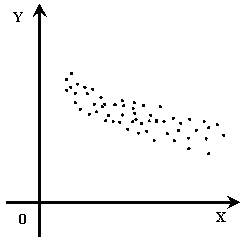
Рис. 7. Пример корреляционного поля (отрицательная корреляция)

Если же в расположении точек нет какой-либо закономерности, то говорят, что в этом случае наблюдается нулевая корреляция.
Линейная парная регрессия. Связь зависимой переменной с одной или несколькими независимыми переменными

описывается с помощью уравнения регрессии
ŷ = f(x₁,x₂,…,x_m). (1)
Это уравнение показывает, каково будет в среднем значение y, если переменные x примут конкретные значения.

Если независимая переменная одна, то регрессия называется парной.

Построение уравнения регрессии включает в себя два этапа:

1) определение вида зависимости (этап спецификации);

2) определение коэффициентов регрессии (этап идентификации).

Предположим, на этапе спецификации установлено, что между величинами x и y существует линейная зависимость. Реальные значения y будут отличаться от этой теоретической зависимости.

В общем случае линейное уравнение связи двух переменных, учитывающее случайные отклонения, можно представить в виде
ŷ = α + β · х + ε, (2)

где ε – отклонение от теоретически предполагаемого значения;

α и β – неизвестные параметры (коэффициенты регрессии).

В уравнении (2) можно выделить две части:

1) систематическую (ŷ = α + β · х), где ŷхарактеризует некоторое среднее значение y для данного значения x;

2) случайную (ε).

Коэффициенты α и βописывают вид зависимости для генеральной совокупности. Так как при выполнении подобных исследований всегда имеют дело с выборочной совокупностью, то истинные значения параметров α и β являются неизвестными и мы можем говорить лишь о их оценках.

Обозначим эти оценки соответственно а и b, тогда уравнение регрессии с оцененными параметрами

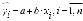, (3)

где n – объем выборки.

Обозначим через e_i отклонение реального значения отклика y_i от теоретически рассчитанного по уравнению ŷ_i.

Параметры a и b уравнения регрессии чаще всего оцениваются с помощью метода наименьших квадратов (МНК).

Суть его состоит в том, чтобы, зная положение точек на плоскости XY, так провести линию регрессии, чтобы сумма квадратов отклонений этих точек от проведенной прямой вдоль оси OY была минимальной.

Математический критерий оценки параметров линейной парной регрессии

.
Условие существования экстремума функции – равенство нулю производной

Раскрыв скобки и выполнив преобразования, получим систему из двух уравнений с двумя неизвестными

Разделив первое уравнение на n, получим

.

То есть метод наименьших квадратов дает прямую, проходящую через точку

.

Решая систему уравнений, получим расчетные формулы для нахождения коэффициентов уравнения регрессии

; (4)

. (5)
Коэффициент линейной корреляции. Величина влияния фактора на исследуемый отклик может быть оценена при помощи коэффициента линейной парной корреляции, характеризующего тесноту (силу) линейной связи между двумя переменными.

Коэффициент линейной парной корреляции

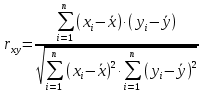. (6)
Коэффициент линейной парной корреляции обладает следующими свойствами:

1) не имеет размерности, следовательно, сопоставим для величин различных порядков;

2) изменяется в диапазоне от –1 до +1. Положительное значение свидетельствует о прямой линейной связи, отрицательное – об обратной. Чем ближе абсолютное значение коэффициента к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент по абсолютной величине превышает 0,7, и слабая, если он менее 0,3 (табл. 7).

Для характеристики тесноты связи можно пользоваться табл. 7.

Таблица 7

Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Характер связи
До │±0,3│	Практически отсутствует
│±0,3│─│±0,5│	Слабая
│±0,5│─│±0,7│	Умеренная
│±0,7│─│±1,0│	Сильная