Добавлен: 12.12.2023
Просмотров: 127
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(УПТ) выделяет постоянную составляющую и изменяет ее полярность, после
чего напряжение измеряется цифровым вольтметром. Если в первом канале,
например, ограничение несимметричное, то импульсы
 и
и  сдвинуты, как
сдвинуты, как показано стрелками на рис.6. Импульс
 станет короче, а импульс
станет короче, а импульс  –
–длиннее, поэтому результирующая постоянная составляющая останется без
изменения.
В фазометре Ф2-16 предусмотрен режим измерения сдвига фаз
 180°.
180°. В этом режиме с помощью переключателя напряжения
 и
и  меняются
меняются местами, на сумматор подается напряжение смещения не –12, а –6 В. Графики напряжений для этого режима показаны на рис.6 справа.
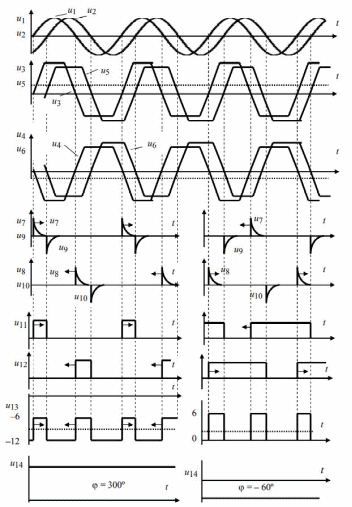
Рисунок 6. Временные диаграммы сигналов внутри фазометра Ф2-16.
В лабораторном макете смонтированы регулируемый фазовращатель,
фазосдвигающий Т-мост и набор из трех линий задержки.
Фазовращатель:
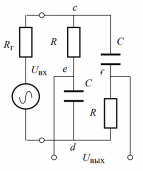
Схема используемого фазовращателя приведена на
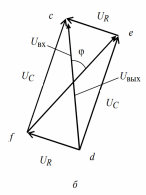
рис.7, а. Векторная диаграмма (рис.7, б) поясняет его работу. Фазовый
угол между напряжениями на конденсаторе и на резисторе равен 90°. Сумма
этих напряжений в данной схеме при любых значениях R и С остается постоянной, равной входному напряжению. Выходное напряжение снимается
между точками e и f фазовращателя. Из диаграммы видно, что при одновременном изменении сопротивлений резисторов R от 0 до
 фазовый сдвиг между входным и выходным напряжениями меняется от 0 до 180°. Амплитуда выходного напряжения остается при этом постоянной, равной амплитуде входного.
фазовый сдвиг между входным и выходным напряжениями меняется от 0 до 180°. Амплитуда выходного напряжения остается при этом постоянной, равной амплитуде входного. Фазовый сдвиг определяется формулой
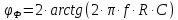
В реальной схеме сопротивления резисторов не могут меняться от 0 до
бесконечности, поэтому фазовый сдвиг в фазовращателе будет изменяться в
п
ределах
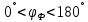 .
.
а
Рисунок 7. Схема и векторная диаграмма напряжений фазовращателя.
Т-мост:
Схема фазосдвигающего Т-моста приведена на рис. 8. Нагрузкой его в данной работе является осциллограф, входное сопротивление
которого много больше выходного сопротивления Т-моста. В этом случае
выражение для фазового сдвига, создаваемого Т-мостом, имеет вид
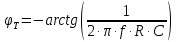
Линии задержки:
Простейшая линия задержки представляет собой ряд
каскадно включенных LC-звеньев (рис. 9). Каждое звено дает временную
задержку
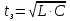 ; общее время задержки линии из n звеньев
; общее время задержки линии из n звеньев 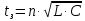 .
.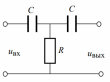
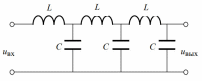
Рисунок 8. Т-мост. Рисунок 9. Линия задержки.
Волновое сопротивление такой линии
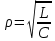 . Для неискаженной передачи сигналов линия задержки должна быть нагружена на сопротивление
. Для неискаженной передачи сигналов линия задержки должна быть нагружена на сопротивление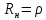 , а полоса ее пропускания должна быть больше ширины спектра сигнала. Фазовый сдвиг, создаваемый линией задержки, может быть вычислен по формуле
, а полоса ее пропускания должна быть больше ширины спектра сигнала. Фазовый сдвиг, создаваемый линией задержки, может быть вычислен по формуле 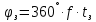 .
.ФЧХ линии задержки представляет собой прямую линию с наклоном,
определяемым временем задержки
 .
.Обработка результатов эксперимента:
1. Измерение сдвига между каналами CH1X и CH2Y осциллографа GOS620 способом элипса.
разберемся как получилось выражение
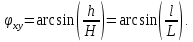
Уравлене элипса в нашем случае запишется следующим образом:
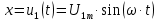
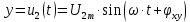
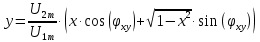
при
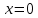
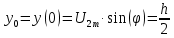 и
и 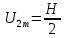
при
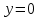
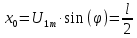 и
и 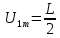
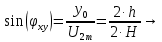
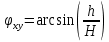
по аналогии получим
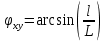
П
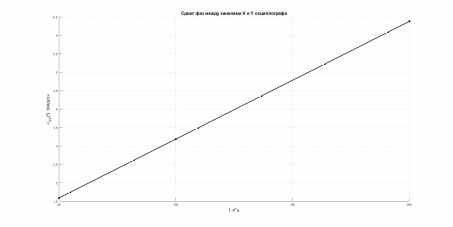 остроим график зависимости
остроим график зависимости 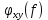 – рис.10.
– рис.10.Рисунок 10. Сдвиг фаз между каналами X и Y осциллографа GOS620.
Как видно из графика, разность фаз между каналами X и Y линейно зависима от частоты. Такой простой род зависимости упрощает дальнейший анализ двух входных гармонических сигналов в режиме отображения XY осциллографа. Также заметим, что с ростом частоты возрастает и вносимый самим социллографом сдвиг фаз, можно сделать вывод, что для анализа гармонических сигналов низких частот метод элипса достаточно хорошо применим, но для более высоких частот следует учитывать инструментальную и систематическую погрешность осциллографа.
2. Градуировка фазовращателя лабораторного макета с помощью
фазометра Ф2-16.
 Построим на одном графике градуировочные кривые фазовращателя
Построим на одном графике градуировочные кривые фазовращателя 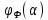 для указанных частот – рис.11.
для указанных частот – рис.11.Рисунок 11. Зависимость разности фаз на входе и выходе фазовращателя.
Из рис.11 можно сделать вывод, что шкала фазовращателя размечена логарифмическим образом и измерения, в общем то, выполнены верно, так как графики по своей форме похожи друг на друга.
3. Измерение фазового сдвига Т-моста нулевым способом.
Измерения для разных частот воздействия проводились с использованием метода элипса (регулировкой фазовращателя добивались стягивания элипса в прямую на осциллограмме, что соответствует разности фаз в 0 на входе X – подключен фазовращатель, и Y – подключен выход с Т-моста). Так как разность фаз, создаваемая фазовращателем зависит от исследуемой частоты воздействия, сделаем следующее:
1. аппрокимируем каждую из 6 кривых на графике рис.11 полиномом 6 степени для большей точности (см. код в MatLab).
2. по эмперическим значениям из протокола получим экспериментальную разность фаз
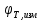 (см. код в MatLab).
(см. код в MatLab).3. найдем по формуле
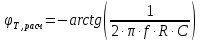 теоретическое значение разности фаз, создаваемой Т-мостом (см. код в MatLab).
теоретическое значение разности фаз, создаваемой Т-мостом (см. код в MatLab).4. построим графики
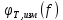 и
и 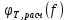 и проанализируем полученные результаты – рис.12.
и проанализируем полученные результаты – рис.12.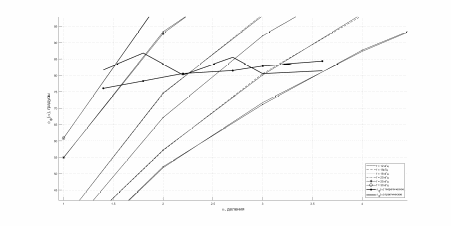
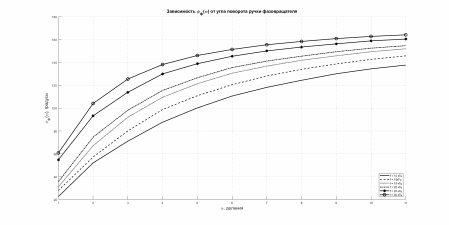
Рисунок 12. На данном графике изображены аппроксимированные и эксперементальные зависимости фазового сдвига фазовращателя от частоты воздействия и велечины деления, поверх них жирными линиями нанесены графики фазовго сдвига на Т-мосте.
Не стоит забывать, что цепь Т-моста имеет емкостной характер, по этому разность фаз < 0. Практический график примерно схож с теоретическим, хоть и с небольшими погрешностями, которые, как мы думаем, являются систематическими и пришли к нам из 2 пункта. Грубых промахов нет – результат можно считать удовлетворительным.
4. Измерение фазочастотных характеристик трех линий задержки
с помощью фазометра Ф2-16.
Проанализируем как LC цепь на рис.9 задерживает/создает разность фаз входного и выходного сигналов – рис 13.
Найдем время задержки для каждой из линий по следующей формуле:
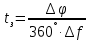
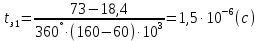
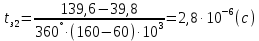
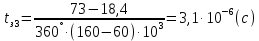
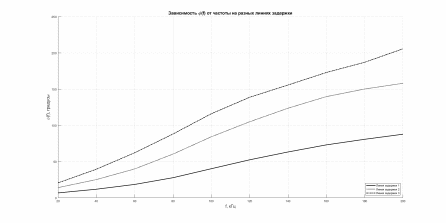
Рисунок 13. Зависимость разности фаз входного и выходного сигналов от частоты на разных линиях задержки.
Вывод: в ходе данной лабораторной работы были изучены методы определения фазовых сдвигов и принцип действия приборов, с которыми производились опыты. Были произведены расчёты по измереным величинам и построены графики зависимостей. Можно сделать вывод, что метод эллипса позволяет достаточно быстро и наглядно найти разность фаз между двумя исследуемыми гармоническими сигналами одной частоты, но при этом дает низкую точность. Также мы пользовались электронным фазометром и по измеренным и обработанным данным из 2 пункта смогли посчитать данные в пункте 3. Схема исследуемого фазовращателя является достаточно непрактичной из-за сложных зависимостей величины разности фаз от градуировки шкалы и частоты входного сигнала.
by:machete©