Файл: Курсовой проект по дисциплине конструкция и прочность авиационных двигателей тема Анализ статической и динамической прочности рабочей лопатки первой ступени турбины гтд тв2117.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 182
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Логарифмируя левую и правую части, получим:
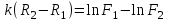 ⇒
⇒⇒
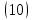
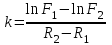 ,
,F1>F2>0; R2>R1>0 ⇒k>0
Для типичных геометрических параметров лопатки турбины первой ступени двигателя ТВ2-117 (Методическое указание к выполнению курсового проекта, 1990): R1=0,400 м; R2=0,525 м; F1=0,00038 м2; F2=0,000124 м2.
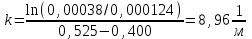
С использованием экспоненциальной аппроксимации (9) зависимости для F(r) распределения напряжений растяжения от центробежной силы примет вид:
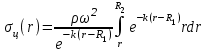
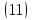
Выделяя постоянные величины в подынтегральном выражении, получим:
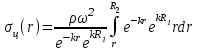
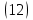
Вынося постоянный множитель
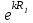 из под знака интеграла, будем иметь:
из под знака интеграла, будем иметь: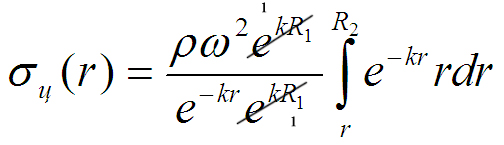
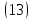
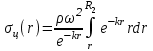
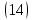
Теперь необходимо этот интеграл взять “по частям”.
Формула интегрирования “по частям” имеет вид:
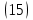
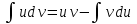
Для того чтобы использовать эту формулу, подынтегральное выражение должно иметь вид
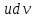 . Перепишем интеграл в формуле (14) в следующем виде:
. Перепишем интеграл в формуле (14) в следующем виде: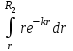
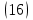
Пусть сомножитель r=u, тогда оставшиеся сомножители
e-kr·dr должны образовать дифференциал
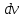 , однако из произведения e-kr·dr дифференциала не получается, поэтому необходимо продифференцировать e-kr по r, и тогда получится:
, однако из произведения e-kr·dr дифференциала не получается, поэтому необходимо продифференцировать e-kr по r, и тогда получится: 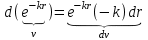
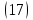
Проявим хитрость: умножим и разделим подынтегральное выражение на –k (имеем право, т.к. –k – постоянная величина) и
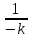 вынесем за знак интеграла:
вынесем за знак интеграла: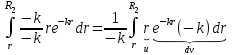
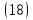
Теперь под знаком интеграла оказалось выражение, к которому можно применить формулу интегрирования по частям:
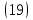
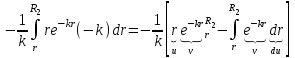

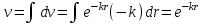
Табличный интеграл:
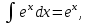 и если принять -k·r=x,тогда (-k)·dr=dx
и если принять -k·r=x,тогда (-k)·dr=dxРасставляя пределы интегрирования для первого слагаемого в правой части выражения (19) получим:
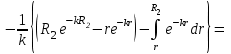
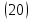 ,
,Для того чтобы вычислить определенный интеграл в формуле (20) снова используем тот же прием: умножим и разделим подынтегральное выражение на (-k) и вынесем
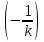 за знак интеграла. В результате получим:
за знак интеграла. В результате получим: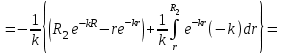
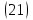

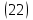
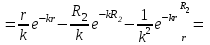
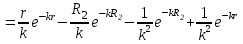
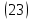
Подставляя полученное выражение (23) в формулу для напряжений
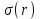 (14), получим:
(14), получим: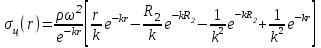
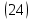
Умножим и разделим правую часть на k2:
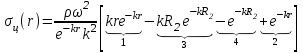
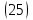
Разделим выражение в квадратных скобках на e-kr и вынесем делитель за скобки:
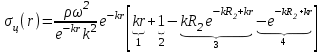
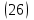
Окончательно получаем:
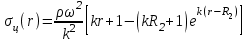
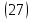
2 Анализ статической и динамической прочности рабочей лопатки первой ступени турбины компрессора
Цель работы заключается в том, чтобы сделать заключение о выполнении или невыполнении условия прочности рабочей лопатки первой ступени турбины, при действии статических нагрузок на взлётном режиме работы двигателя в условиях, соответствующих исходным данным.
В случае выполнения условия прочности необходимо определить наиболее слабое с точки зрения прочности сечение лопатки.
В данном случае для анализа статической и динамической прочности используется рабочая лопатка первой ступени турбины ГТД ТВ2-117 изображенные на рисунках 1-4.
 |
| Рисунок 1 – Двигатель ТВ2-117 вид слева [фото автора] |
| |
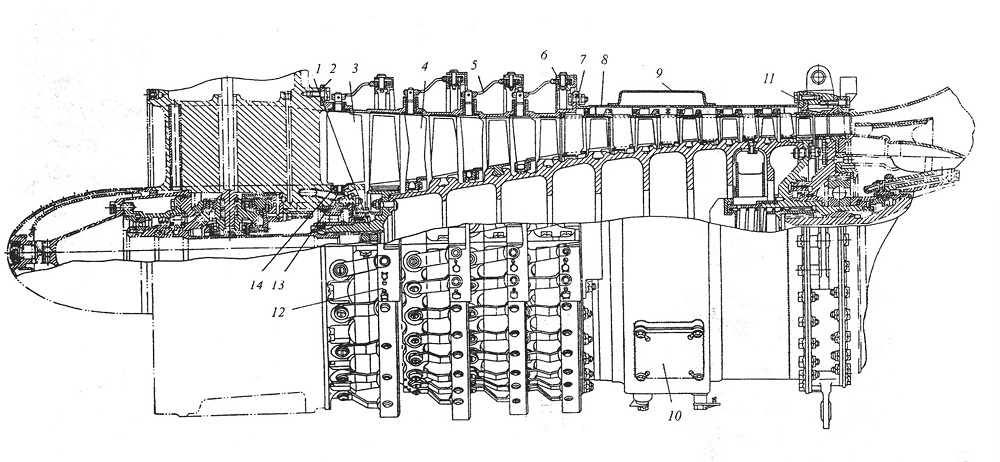 |
| Рисунок 2 – Компрессор двигателя ТВ2-117 [9] |
 |
| Рисунок 3 – Двигатель ТВ2-117 вид спереди [9] |
2.1 Исходные данные
В данном случае для анализа статической прочности используется рабочая лопатка первой ступени турбины ГТД ТВ-2-117, после 100 часов нагрузки взлётного режима.
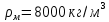 - плотность материала лопатки;
- плотность материала лопатки;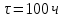 - время работы двигателя на взлётном режиме;
- время работы двигателя на взлётном режиме;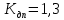 - минимально допустимый запас прочности;
- минимально допустимый запас прочности;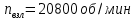 - частота вращения ротора на взлётном режиме;
- частота вращения ротора на взлётном режиме;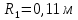 - радиус корневого сечения пера лопатки;
- радиус корневого сечения пера лопатки;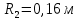 - радиус концевого сечения пера лопатки;
- радиус концевого сечения пера лопатки;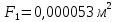 - площадь поперечного сечения в корневой части пера лопатки;
- площадь поперечного сечения в корневой части пера лопатки;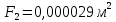 - площадь поперечного сечения в концевой части пера лопатки;
- площадь поперечного сечения в концевой части пера лопатки;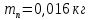 - сосредоточенная масса бандажной полки лопатки;
- сосредоточенная масса бандажной полки лопатки;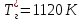 - полная температура на входе первой ступени турбины.
- полная температура на входе первой ступени турбины.2.2 Ход работы
Определим шаг изменения радиуса сечений по длине пера лопатки используя формулу:
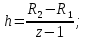 (28)
(28)где z – установленное число сечений.
Пусть z = 6, тогда согласно формуле получим:
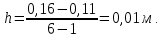
Получим шесть значений радиуса сечений по длине пера лопатки:
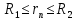
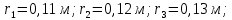
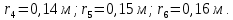
Определим напряжения, возникающие от действия центробежных сил, действующие на массу пера лопатки в n - ом сечении по закону:
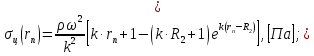 29)
29)где
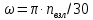 – циклическая частота вращения ротора;
– циклическая частота вращения ротора;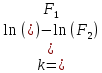 – коэффициент сужения лопатки;
– коэффициент сужения лопатки;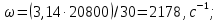
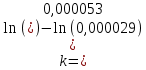
Пример расчета:
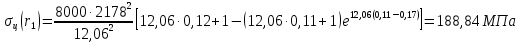
Определим значения напряжений от центробежных сил, действующих на массу бандажной полки в каждом сечении пера лопатки. Расчёт производится по формуле:
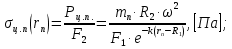 (30)
(30)где
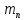 – сосредоточенная масса бандажной полки.
– сосредоточенная масса бандажной полки.Пример расчета :