Файл: Курсовой проект по дисциплине конструкция и прочность авиационных двигателей тема Анализ статической и динамической прочности рабочей лопатки первой ступени турбины гтд тв2117.docx

C₁ = a+b·i, C₂ = a-b·i(при сложении С₁ и С₂ их мнимые части взаимно уничтожаются).

Заметим также, что сомножители e^iωt и e^-iωtв слагаемых правой части уравнения (А.7) также являются комплексно сопряженными. В этом можно убедиться, записав их в тригонометрической форме:

	eiωt = cos(ωt) + i· sin(ωt),	(А.9)
	e-iωt = cos(ωt) - i· sin(ωt).	(А.10)

Используя правила умножения комплексных чисел, можно показать, что комплексно сопряженными являются и входящие в правую часть уравнения (А.7) слагаемые C₁·e^iωtи C₂·e^-iωt.

Таким образом, из уравнения (А.7) следует, что решение исходного уравнения (А.3) лежит в комплексной плоскости и представляет собой совокупность сумм двух комплексно сопряженных чисел Z₁(ωt) = C₁·e^iωtи Z₂(ωt) = C₂·e^-iωt. Графическая иллюстрация этого решения приведена на рисунке А.2.



Рисунок А.2 – Графическая иллюстрация решения дифференциального уравнения, описывающего собственные колебания простейшей колебательной системы с одной степенью свободы.
Векторы Z₁(ωt) и Z₂(ωt), изображающие соответствующие комплексные числа, располагаются симметрично относительно действительной оси x под углами ωtи - ωt к ней. Геометрическая сумма векторов Z₁(ωt) и Z₂(ωt) определяет координату свободного конца упругого стержня в данный момент времени t. Углы ωtи - ωtизменяются пропорционально времени t. Векторы Z₁(ωt) и Z₂(ωt) описывают процесс колебаний, вращаясь вокруг начала координат комплексной плоскости в противоположные стороны. Параметр ω имеет смысл угловой скорости вращения этих векторов. В теории колебаний ω называется круговой или угловой частотой и имеет размерность рад/с.

---

С помощью соотношений (А.9) и (А.10) полученное на комплексной плоскости решение (А.7) может быть преобразовано в тригонометрическую форму. Подставляя соотношения (А.9) и (А.10) в решение (А.7), получим:

x(t) = (C1 + C2)·cos(ωt) + i·( C1 - C2)· sin(ωt).

(А.11)

Выбранные нами ранее начальные условия t = 0, x(0) = x₀ позволили определить, что C₁ + C₂ = x₀. Рассмотрим теперь момент времени t_±π/2, соответствующий углам поворота векторов Z₁ и Z₂, равным π/2 и - π/2, соответственно. Из рисунка 2 видно, что в момент времени t_±π/2 векторы Z₁ и Z₂ лежат на мнимой оси yи направлены в разные стороны. При этом действительные части x(t_±π/2) = 0. Тогда в соответствии с полученным решением (А.7):

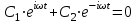(А.12)

откуда:

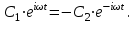(А.13)

Комплексно сопряженные числа e^iωt и e^-iωt в общем виде могут быть представлены следующим образом:

	eiωt = a + b·i,	(А.14)
	e-iωt = a - b·i.	(А.15)

Подставив выражения (А.14) и (А.15) в уравнение (А.13), получим:

С1·a +С1· b·i = - C2·a + C2·b·i.

(А.16)

Из рисунка А.2 видно, что в рассматриваемый момент времени t_π/2 комплексные числа Z₁ = С₁·a +С₁· b·iи Z₂ = - С₂·a +С₂· b·i являются чисто мнимыми, при этом их действительные части равны нулю:

---

С₁·a = 0, - С₂·a = 0. Поэтому уравнение (А.16) может быть записано в следующем виде:

С1· b·i = C2·b·i,

(А.17)

откуда следует, что С₁ = С₂. Учитывая полученный ранее результат C₁ + C₂ = x₀, определяем значения постоянных С₁ и С₂ для выбранных начальных условий: С₁ = С₂ = x₀/2. Возвращаясь к тригонометрической форме решения исходного дифференциального уравнения (А.11) и учитывая равенство С₁ = С₂, получаем:

x(t) = (C1 + C2)·cos(ωt).

(А.18)

Здесь сумма коэффициентов C₁ + C₂ представляет собой амплитуду колебаний А, равную максимальным по модулю отклонениям свободного конца упругого стержня : C₁ + C₂ = A = max {| x(t)|}. С учетом этого равенства можно записать решение дифференциального уравнения, описывающего собственные колебания простейшей колебательной системы с одной степенью свободы в окончательном виде:

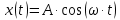(А.19)

где ω - циклическая частота колебаний.



Рисунок А.3 – Зависимость координаты х свободного конца стержня от времени t в процессе свободных колебаний без затухания

---