Файл: В задачах 4 7 составить экономикоматематические модели 4.docx
Добавлен: 12.12.2023
Просмотров: 224
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построим математическую модель задачи. Пусть х1-количество изделий вида 1, шт, х2 - количество изделий вида 2, шт запланированных к производству.Для их изготовления потребуется (7 х1 +3х2) единиц ресурса I, (8х1 +12х2) единиц ресурса II, (6х1 +8х2) единиц ресурса III. Так как, потребление ресурсов I, II, III не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
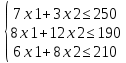

Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х1 и х2.
Суммарная прибыль составит 18х1 от реализации продукции 1 и 16х 2 от реализации продукции 2, то есть : L = 18х1 +16х 2. →max.
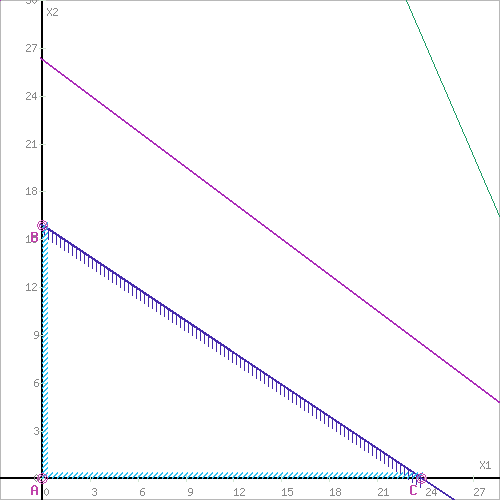
Построим область допустимых решений
| В первую очередь, найдем область допустимых решений, т.е. точки x1 и x2 , которые удовлетворяют системе ограничений. |
| По условию задачи x1 которые принадлежат первой четверти. | |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
Шаг 2
| Рассмотрим неравенство 2 системы ограничений. |
| 8 x1 | + 12 x2 | | 190 |
| Построим прямую. |
| Заменим знак неравенства на знак равенства . |
| 8 x1 | + 12 x2 | = | 190 |
| Преобразуем уравнение следующим образом . |
| x1 | + | x2 | = 190 |
| | | ||
| 1/8 | 1/12 |
| Каждый член уравнения разделим на 190 . |
| x1 | + | x2 | = 1 |
| | | ||
| 95/4 | 95/6 |
| Мы получили уравнение прямой в отрезках. Данная форма записи позволяет легко нарисовать прямую. На оси x1 рисуем точку с координатой 95/4 . На оси x2 рисуем точку с координатой 95/6 . Соединяем полученные точки и получаем необходимую прямую. |
| Какие точки нас интересуют? |
| 8 x1 | + 12 x2 | | 190 |
| 12 x2 | | -8 x1 | + 190 |
| x2 | | -2/3 x1 | + 95/6 |
| Знак неравенства меньше или равно нуля, следовательно, нас интересуют точки лежащие ниже построенной нами прямой. |
| Шаг 3 |
| Рассмотрим неравенство 3 системы ограничений. |
| 6 x1 | + 8 x2 | | 210 |
| Построим прямую. |
| Заменим знак неравенства на знак равенства . |
| 6 x1 | + 8 x2 | = | 210 |
| Преобразуем уравнение следующим образом . |
| x1 | + | x2 | = 210 |
| | | ||
| 1/6 | 1/8 |
| Каждый член уравнения разделим на 210 . |
| x1 | + | x2 | = 1 |
| | | ||
| 35 | 105/4 |
| Мы получили уравнение прямой в отрезках. Данная форма записи позволяет легко нарисовать прямую. На оси x1 рисуем точку с координатой 35 . На оси x2 рисуем точку с координатой 105/4 . Соединяем полученные точки и получаем необходимую прямую. |
| Какие точки нас интересуют? |
| 6 x1 | + 8 x2 | | 210 |
| 8 x2 | | -6 x1 | + 210 |
| x2 | | -3/4 x1 | + 105/4 |
| Знак неравенства меньше или равно нуля, следовательно, нас интересуют точки лежащие ниже построенной нами прямой. |
| Шаг 4 |
| Вернемся к нашей исходной функции L . |
| L = | 18 x1 | + 16 x2 |
| Допустим значение функции L равно 1 (абсолютно произвольно выбранное число), тогда |
| 1 = | 18 x1 | + 16 x2 |
| Данное уравнение является уравнением прямой на плоскости. |
| Из курса аналитической геометрии известно, что данная прямая перпендикулярна вектору, координатами которого являются коэффициенты функции, а именно вектору ON = (18,16). |
| Следовательно, с геометрической точки зрения, функция L изображается как множество прямых перпендикулярных вектору ON = (18,16). |
| Построим вектор ON = (18,16). |
| Вектор ON изображен розовым цветом. |
| Значение функции L будет возрастать при перемещении прямой в направлении вектора ON. |
| Диапазон перемещения прямой НЕ от точки O до точки N, а именно, в направлении от точки O к точке N. |
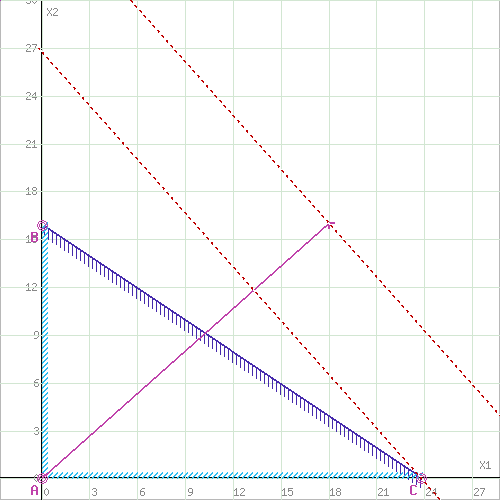
| Будем перемещать прямую, перпендикулярную вектору ON, до тех пор, пока она полностью не пройдет область допустимых решений. |
| В нашем случае, касание прямой, перед выходом из области допустимых решений, произойдет в вершине C (95/4,0). В точке C значение функции L будет наибольшим. |
| Ответ : |
| Lmax = 855/2 |
| x1 = 95/4 x2 = 0 |
Значит необходимо выпускать 95/4 штук изделий вида 1, чтобы получить максимальную прибыль в размере 855/2 ден ед
Через точку С(95/4,0) определяющую оптимальный план проходят прямые ВС и АС. Соответствующие им ограничение 8x1+12x2≤190 является активным, а соответствующий вид сырья номер 2 является дефицитным. Рассмотрим увеличение запасов сырья номер 2( то есть правой части ограничения). Это увеличение можно представить как перемещение прямой ВС параллельно самой себе до точки пересечения прямой 6х1+8х2=210. Тогда ограничение ВС остается активным, точка (35,0) будет определять оптимальное решение, ресурс 2 увеличиться до 8*35+12*0=280. При этом величина дохода составит 18*35+16*0=630 ден ед. Таким образом увеличение объема ресурса номер 2 с190 до 280 приведет к увеличению выпуска продукции первого типа от 23,75 до35 и увеличению прибыли от 855/2 до 630 ден ед.
Определим диапазон изменения запасов недефицитных ресурсов, при котором оптимальное решение не меняется. Через точку С не проходят прямые 7х1+3х2=250,6х1+8х2=210, являются пассивными, а соответствующие им ресурсы недефицитными. Уменьшение запаса сырья номер 2 с 250 до 166,25 не изменить оптимального плана. Так же уменьшение запаса сырья номер 3 с 210 до 142,5 не изменит оптимального плана. Однако еще более существенное уменьшение запасов сырья первого и второго видов приведет к уменьшению прибыли и другому оптимального плану.