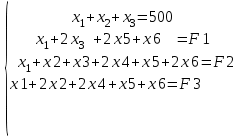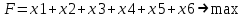Файл: В задачах 4 7 составить экономикоматематические модели 4.docx
Добавлен: 12.12.2023
Просмотров: 222
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| ограничение | Изменение от | до | Оптимальные значения | Значение целевой функции |
| 8х1+12х2=190 | 190 | 280 | (23,75,0)⇒(35,0) | 855/2⇒630 |
| 7х1+3х2=250 | 250 | 142,5 | (23,75,0) | 855/2⇒855/2 |
| 6х1+8х2=210 | 210 | 142,5 | (23,75,0) | 855/2⇒855/2 |
Задача №2. Определение наиболее выгодного ресурса.
Условие из задачи №1, вопрос – какому из ресурсов(питательных веществ) следует отдать предпочтение при вложении дополнительных средств? Необходима сводная таблица по результатам расчетов теневой цены для всех ограничений.
Решение.
Вычислим ценность дополнительной единицы дефицитного ресурса
Y=
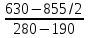 =2.25
=2.25Так как внашей задаче дефицитный ресурс один то дополнительные средства и выгодно вкладывать в закупку второго ресурса.
Задача №3. Определение пределов изменения коэффициентов целевой функции.
Условие из задачи №1, вопросы:
-
Каков диапазон изменения коэффициентов целевой функции, при котором не происходит изменение оптимального решения? Т.е. как можно варьировать цены на выпускаемый продукт(корм) при неизменной прибыли от продажи продукта или при неизменной стоимости рациона? -
На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным, и, наоборот, дефицитный ресурс сделать недефицитным?
Решение.
Определим диапазон изменения цены на продукцию вида1 . Пусть цена на продукцию вида 2 не меняется .Тогда линия уровня с1х1+16х2=а может совпадать с прямой ВС у которой угловой коэффициент -2/3. У параллельных прямых угловые коэффициенты совпадают, поэтому -2/3=-с1/16⇒с1=32/3. При этому доход фирмы станет равным 32/3*23,75+0=253,333, то есть упадет.
Если же цену на продукцию вида 1 оставить без изменения, а цену 2 менять, тогда линия уровня 18х1+с2х2=а может совпасть с прямой ВС. Тогда с2=3. При этом доход фирмы станет равным 18*23,75+0=855/2, то есть останется на прежнем уровне. Значит от цены на товар 2 вообще не зависит прибыль предприятий, а ценуна товар 2 изменять нельзя так как это приведет к уменьшению прибыли.
Задача
Предприятие имеет три группы станков, объемы загрузки которых ограничены и составляют соответственно 30, 24 и 3 станков-часов. Производительность каждой группы станков по двум типам деталей А и Б составляет по деталям А 10, 15 и 20 деталей в час, а по деталям Б-20, 40 и 60 деталей в час. Найти время загрузки каждой группы станков, чтобы получить максимальное общее количество деталей обоих типов, и соответствующее число каждого типа.
Решение.
Составим математическую модель задачи
x1 - время работы станка 1 для производства продукции А
x2 - время работы станка 2 для производства продукции А
x3 - время работы станка 3 для производства продукции А
Если станок производит детали 2-х типов, то общее время его работы равно суммарному времени работы по изготовлению деталей каждого из двух типов.
Целевая функция:
f(x)=10x1+20(30-x1)+15x2+40(24-x2)+20x3+60(3-x3)=-10x1-25x2-40x3+1740→max
и ограничения:
| | | x1 | | | | | | | ≤ | | 30 | | (1) |
| | | | | | x2 | | | | ≤ | | 24 | | (2) |
| | | | | | | | | x3 | ≤ | | 30 | | (3) |
x1, x2, x3 ≥ 0
Решим задачу симплекс методом
Шаг:1
Избавимся от неравенств в ограничениях, введя в ограничения 1, 2, 3 неотрицательные балансовые переменные s1, s2, s3.
| | | x1 | | | | | | | + | | s1 | | | | | | | = | | 30 | | (1) |
| | | | | | x2 | | | | | | | + | | s2 | | | | = | | 24 | | (2) |
| | | | | | | | | x3 | | | | | | | + | | s3 | = | | 30 | | (3) |
x1, x2, x3, s1, s2, s3 ≥ 0
Шаг:2
Ищем в системе ограничений базисные переменные.
Из последней системы ограничений можно выделить базисные переменныеs1,s2,s3.
| |
Теперь мы можем сформировать начальную симплекс-таблицу.
Шаг:3
Начальная симплекс-таблица
| БП | x1 | x2 | x3 | s1 | s2 | s3 | Решение | Отношение |
| s1 | 1 | 0 | 0 | 1 | 0 | 0 | 30 | -- |
| s2 | 0 | 1 | 0 | 0 | 1 | 0 | 24 | -- |
| s3 | 0 | 0 | 1 | 0 | 0 | 1 | 30 | -- |
| Q | -10 | -25 | -40 | 0 | 0 | 0 | -1740 | -- |
В таблице записано оптимальное решение, т.к. в строке целевой функции нет положительных коэффициентов.
Ответ:
| Оптимальное значение функции Q(x)= | 1740 |
достигается в точке с координатами:
| x1= | 0 |
| x2= | 0 |
| x3= | 0 |
| s1= | 30 |
| s2= | 24 |
| s3= | 30 |
Значит время работы каждого станка для производства продукции А равно 0.Значит надо производить только изделия вида В. Время работы каждого станка для производства продукции В соответственно равно 30,24,3 часов соответственно. При этом максимальное общее количество деталей обоих типов составит 1740 штук. Первый станок даст 600 деталей типа В, второй 960 деталей типа В и третий 180 деталей типа В.
Для изготовления изделия требуется три планки - одна размером 1,2 м и две по 1,5 м каждая. Для этой цели можно использовать имеющийся запас реек-400 штук, длиной по 5 м каждая, и 100 штук, длиной по 6,5 м каждая. Определите, как разрезать все эти рейки, чтобы получить наибольшее количество изделий.
Решение.
Определим сначала все возможные способы распила реек, указав соответствующее число получающихся при этом планок и остаток.
Способы распила реек
| Способ распила | Число получающихся планок | Остаток | ||
| 1,2 м | 1,5 м | 1,5 | ||
| 1(дл 5) | 1 | 1 | 1 | 0,8 |
| 2(дл 5) | - | 1 | 2 | 0,5 |
| 3(дл 5) | 2 | 1 | - | 1,1 |
| 4(дл 6,5) | - | 2 | 2 | 0,5 |
| 5(дл 6,5) | 2 | 1 | 1 | 1,1 |
| 6(дл 6,5) | 1 | 2 | 1 | 0,8 |
Через хi обозначим число реек распиливаемых i-м способом,
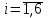 .
. Обозначим через Fk фактическое количество заготовок k, то есть
F1 – фактическое количество заготовок 1,20 м;
F2 – фактическое количество заготовок 1,50 м;
F3 – фактическое количество заготовок 1,50 м.
Обозначим через N1=400 количество материала (количество реек длиной 5 м), которое следует разрезать, чтобы выполнить заказ.
Обозначим через N2=100 количество материала (количество реек длиной 6,5 м), которое следует разрезать, чтобы выполнить заказ.
Тогда экономико-математическая модель задачи будет иметь вид: