МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Институт финансов, экономики и управления

(наименование института полностью)

Управление персоналом

(Наименование учебного структурного подразделения)

38.03.03

(код и наименование направления подготовки / специальности)

Управление персоналом

(направленность (профиль) / специализация)

Практическое задание №2
по учебному курсу «Экономика 1»

^{(наименование учебного курса)}
Вариант 4

Обучающегося	А.Е. Калиткина
	(И.О. Фамилия)
Группа	УПбвд-2101а
Преподаватель	Ю.А. Анисимова
	(И.О. Фамилия)

Тольятти 2023

Задача 1. На рынке функция предложения некоторой совершенно конкурентной фирмы задана уравнением

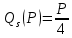
Значение постоянных издержек фирмы составляет 1000 ден. ед. Известно, что в некий период времени рыночная цена установилась на уровне 200 ден. ед. Определите величину максимальной прибыли фирмы при заданной цене. Постройте график предложения фирмы с помощью программы Excel.

---

Решение:

1. 
   Оптимальный объем, при котором фирма максимизирует прибыль, определяется из условия : …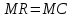
   

Оптимальный объем, при котором фирма максимизирует прибыль, определяется из условия:

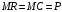
Величина прибыли при P=200 ден.ед. равна ,

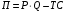предложение фирмы ден.ед,
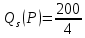
выручка TR=P*Q=50*200=10000 ден.ед., TC=FC+VC=200+1000=1200 величина максимальной прибыли фирмы при заданной цене PR=TR-TC=11000-1200=9800 ден.ед.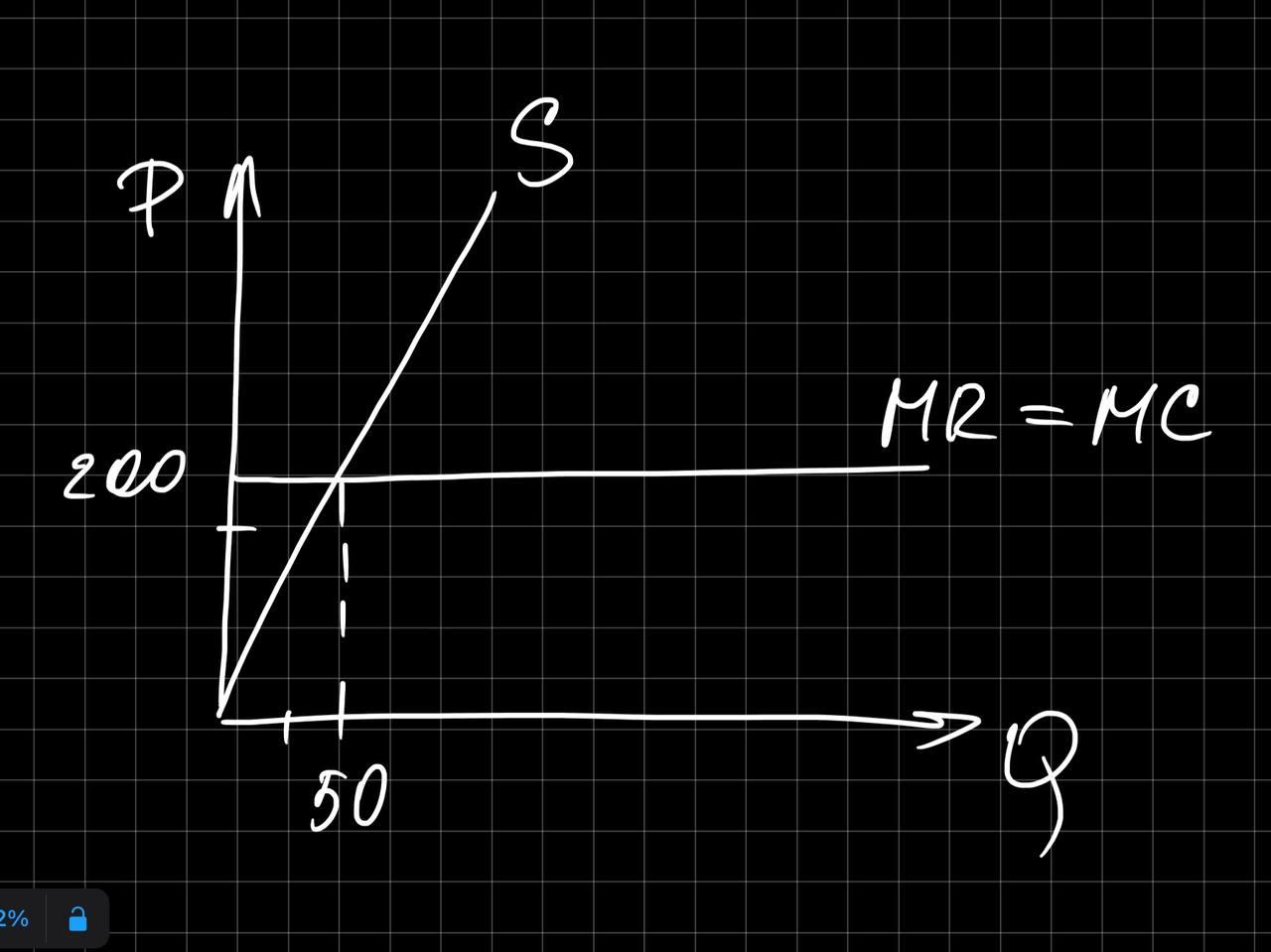


Задача 2. Фирма действует в условиях несовершенной конкуренции. Функция предельной выручки (дохода) задана условием 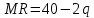. При этом зависимость общих издержек от объема выпуска принимает вид 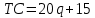. Определите, какой степенью власти на рынке обладает фирма (индекс Лернера).

Решение:

1. 
   Оптимальный объем определяется из условия :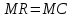
   

MC=(TC(Q))’=20

MR=MC

40-2q=20

Q=10

2. 
   Подставляем значение рассчитанного объема в функцию предельных издержек: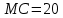
   
3. 
   Из функции предельного дохода (выручки)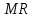 фирмы находим значение цены :
   

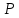Для линейной кривой предельного дохода вида 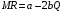функция спроса принимает вид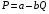 P=40-Q=> P=30.

4. 
   Подставляем рассчитанные значения предельных издержек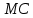 и цены 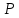в формулу индекса Лернера: ….
   

---

Индекса Лернера (степень власти фирмы на рынке) определим по формуле:



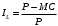
L=(30-20)/30=1/3

Значение индекса Лернера 1/3 что свидетельствует о том, что фирма занимает 1/3 рынка и скорее всего функционирует в условиях олигополии, когда на рынка присутствует несколько крупных фирм.
Ответ: 1/3

Задача 3. Производственная функция фирмы имеет вид: 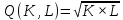. Ставка зарплаты равна значению 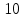ден. ед., а ставка арендной платы за капитал – 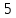ден. ед. Уровень выпуска равен 40 ед. Какой будет оптимальная комбинация ресурсов 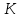и ?

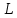Решение:

Для определения оптимальной комбинации факторов производства необходимо рассчитать равновесие фирмы:

при оптимальной комбинации ресурсов будет выполняться равенство:

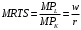(2)

• 
  При объёме Q=20 выполняется равенство 40=(KL)^0,5 => K=1600/=> MRTS = 1600/(L)^2
  
• 
  1600/(L)^2=10/5 => L=20*(2)^1/2 (20 корней из 2)
  
• 
  K=2*L=40*(2)^1/2 ( 40 корней из двух)
  

• 
  Ответ: L=20*(2)^1/2 (20 корней из 2)
  
• 
  K=2*L=40*(2)^1/2 ( 40 корней из двух)
  

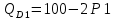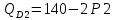Задача 4. Фирма-монополист продает свою продукцию на двух сегментах рынка с различной эластичностью спроса и . Функция общих затрат принимает вид .

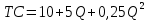Общий объем спроса на продукцию фирмы-монополиста .

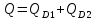Рассчитайте:

– значения цен на каждом из сегментов, при которых фирма-монополист получит максимум прибыли;

– объем продаж на каждом из сегментов и прибыль фирмы-монополиста при запрещении ценовой дискриминации.

Решение:

Максимальную прибыль фирма – монополист получит при соблюдении равенства:



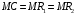
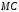- есть производная функции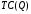

---

MC=5+0,5Q . Из условия 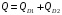MC=5+0,5Q1+0,5Q2.

Для линейной кривой предельного дохода вида функция спроса принимает вид

Выразим функции спроса в виде обратных:

Qd1=100-2P1 => Pd1=50-0,5P1

Qd2=140-2P2 => Pd2=70-0,5P2

Соответствующие функции 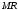будут выглядеть как :

MR1=50-Q1;

MR2=70-Q2.

Так как равенство соблюдается во всех сегментах можно составить систему уравнений: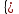

;

;

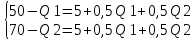Решая систему:

90-390-9Q2=Q2

10Q2=300

Q2=30 => Q1=130-3*30=40

Рассчитаем оптимальные цены при таком количестве объема:

P1=50-0,5*40=30;

P2=70-0,5*30=55

Ответ: 1) цены

P1=50-0,5*40=30;

P2=70-0,5*30=55

2) объёмы

Q2=30 Q1=40

---

Смотрите также файлы

• Железнодорожные пути являются объектами какой опасности а пониженной.docx

• Путешествие по сказкам.docx

• Дипломная работа Метод тестирования как средство педагогического контроля обученности старшеклассников оглавление.docx

• Реферат по дисциплине Физическая культура на тему Значение физической культуры и спорта в жизни человека.doc

• Основная часть 6 1Анализ предметной областИ.docx