Файл: Реферат по предмету Информатика На тему Системы счисления Выполнен(а) студентом.doc
Добавлен: 12.12.2023
Просмотров: 22
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
НАИМЕНОВАНИЕ УЧЕБНОГО УЧРЕЖДЕНИЯ
РЕФЕРАТ
по предмету: Информатика
На тему:Системы счисления
Выполнен(а) студентом
____________________________________________
(фамилия, имя, отчество)
Группа № ___________
Специальность ______________________________
Проверил: __________________________________
(ученая степень, ученое звание)
________________ ____________________
(подпись, дата) (инициалы, фамилия)
Е
1. Перевод чисел из одной системы счисления в другую
Современные вычислительные машины оперируют с информацией, представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления, а в качестве промежуточных систем счисления используются восьмеричная и шестнадцатеричная.
Система счисления (СС) – совокупность символов и правил для записи чисел.
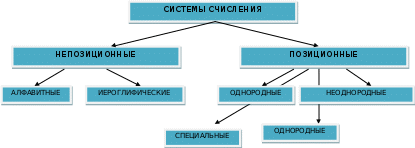
СС разделяются на позиционные и непозиционные.
Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции (места) в числе (арабская система счисления).
Примером позиционной системы счисления является десятичная система счисления, которая располагает только десятью цифрами – 0,1,2,…,9 – но это не мешает представить с их помощью любое число.
Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа, например, римская система счисления.
Одно и то же число можно представить в различных системах счисления. Запись числа при этом различна, а значение остается неизменным. Несмотря на то, что десятичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных элементах, т.к. реализовать на аппаратном уровне элементы с 10 четко различимыми состояниями сложно. По этой причине ЭВМ строятся на базе двоичных цифровых устройств: триггеров, регистров, счетчиков, логических элементов и т.д.
Двоичная, восьмеричная и шестнадцатеричная системы счисления относятся к так называемой «машинной группе». Каждая система счисления из этой группы применяется в различных случаях, а именно:
- двоичная – используется для организации преобразования информации, кодирования дискретного сигнала, потребителем которого является вычислительная техника, поскольку двоичный сигнал проще реализовать на аппаратном уровне;
- восьмеричная и шестнадцатеричная – используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.
Десятичная система применяется в ЭВМ для ввода данных и вывода на устройства печати и на экран дисплея.
Правила записи и выполнения различных операций во всех позиционных СС одинаковы, эти системы счисления отличаются друг от друга только основанием. Основание системы счисления – это количество цифр (символов), используемых для записи любого числа, так:
- в десятичной системе счисления используется десять цифр – 0 9;
- в двоичной системе счисления используются две цифры – 0 1;
- в восьмеричной системе – восемь цифр – 0 7;
- в шестнадцатеричной системе счисления задействовано шестнадцать символов – цифры 0 9 и буквы латинского алфавита A, B, C, D, E, F для записи чисел 10, 11, 12, 13, 14, 15 соответственно.
Следует заметить, что основание системы счисления в своей системе счисления записывается как единица старшего разряда – «10».
2. Перевод чисел из десятичной системы счисления в систему счисления с основанием "b"
Для перевода чисел из одной системы счисления в другую существуют определенные правила. Они различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.
Иначе говоря, в систему счисления с основанием "b" целая и дробная части десятичного числа переводятся отдельно, по разным правилам.
Алгоритм перевода целого числа (целой части) десятичного числа в систему счисления с основанием "b" реализуется посредством выполнения следующих шагов:
1. Разделить нацело исходное десятичное число на основание "b", т.е. получить частное и остаток. Остаток от деления зафиксировать.
2. Полученное частное вновь делить на основание "b" остаток зафиксировать.
Процедуру продолжать до тех пор, пока частное не станет равным нулю.
3. Записать полученные остатки снизу вверх в порядке, обратном их получению.
Результатом перевода должно быть целое число.
ПРИМЕР 1.1. Перевести десятичное число 75 в двоичную систему счисления
(b = 2). Последовательные деления дают следующие результаты:

Таким образом, записывая остатки от деления, начиная с последнего, получаем число 75 в двоичной системе: 1001011.
ПРИМЕР 1.2. Перевести десятичное число 75 в восьмеричную (b=8) и шестнадцатеричную систему счисления (b = 16). Производя аналогичные вычисления, получаем:
| b=8 | b=16 |
| 75:8=9 (остаток 3) 9:8=1 (остаток 1) 1:8=0 (остаток 1) Десятичное число 75 в 8-ричной СС будет записано - 113 | 75:16=4 (остаток 11, или в 16-ричной СС – В) 4:16=0 (остаток 4) Десятичное число 75 в 16-ричной СС будет задано – 4В |
Заметим, чем больше основание системы счисления, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа в позиционных системах счисления.
Алгоритм перевода правильной дроби (дробной части) десятичного числа в систему счисления с основанием "b" заключается в следующем:
1. Умножить исходное десятичное число на основание "b". Зафиксировать целую часть полученного произведения.
2. Дробную часть полученного числа вновь умножить на основание "b", целую часть полученного произведения зафиксировать и т.д. Последовательно повторять умножение. (Перед каждым умножением целую часть предыдущего результата следует обнулить).
3. Завершить процесс последовательных умножений либо при получении нулевой дробной части в очередном произведении, либо при достижении требуемой точности (число умножений определяет число знаков дробной части числа в СС с основанием "b").
4. Справа от запятой записать зафиксированные целые части в той последовательности, в которой они получены.
ПРИМЕР 1.3. Перевести десятичное число 0,7 в двоичную систему счисления с восемью знаками после запятой. Последовательные умножения дают следующие результаты:

Таким образом, результат с точностью до восьмого знака: 0,10110011.
При записи чисел для различия систем счисления будем использовать подстрочный индекс справа от числа:
- для двоичных чисел – в виде цифры 2;
- для восьмеричных чисел – в виде цифры 8;
- для шестнадцатеричных чисел – в виде числа 16.
ПРИМЕР 1.4. Перевести десятичное число 0,7 в восьмеричную (b=8) и шестнадцатеричную СС (b = 16) с двумя знаками после запятой.
| b=8 | B=16 |
| 0,7∙8=5,6 (целая часть 5) 0,6∙8=4,8 (целая часть 4) Получим: 0,710=0,548 | 0,7∙16=11,2 (целая часть В) 0,2∙16=3,2 (целая часть 3) Получим: 0,710=0,В16 |
В том случае, когда исходное число содержит как дробную, так и целую части, их следует перевести по отдельности из десятичной СС в СС с основанием "b" и записать в результирующем числе соответственно слева и справа от запятой.
Следовательно, результат перевода десятичного числа 75,7 в двоичную, восьмеричную и шестнадцатеричную системы счисления будет:
Схемы
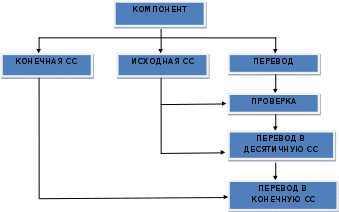
Список литературы
-
Алфутова Н. Б., Устинов А. В. Алгебра и теория чисел: Сборник задач. — М.: МЦНМО, 2009. -
Андреева Е., Фалина И. Системы счисления и компьютерные арифметика. — М.: Лаборатория базовых знаний, 2010. -
Булос Д., Джефр и Р. Вычислимость и логика. — М.: Мир, 2012. -
Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 2010. -
Воробьёв Н. Н. Признаки делимости. — М.: Наука, 2010. — (Популярные лекции по математике. Вып. 39). -
Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 2010. -
Гарднер М. Математические головоломки и развлечения / Пер. с англ. Ю. А. Данилова / Под ред. Я. А. Смородинского. — М.: Мир, 2010. -
Гарднер М. Математические досуги / Пер. с англ. Ю. А. Данилова / Под ред. Я. А. Смородинского. — М.: Мир, 2010. -
Гарднер М. Математические новеллы / Пер. с англ. Ю. А. Данилова / Под ред. Я. А. Смородинского. — М.: Мир, 2009. -
Гашков С. Б., Чубариков В. Н. Арифметика, алгоритмы, сложность вычислений. — М.: Высшая школа, 2000.