ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание №2
по учебному курсу «_Высшая Математика 2»
(наименование учебного курса)
Вариант 6 (при наличии)
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
| № п/п | Задача | Ответ |
| 1. | Рассчитать наибольшее и наименьшее значения функции на заданном отрезке: 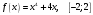 | 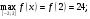 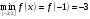 |
| 1) Найти первую производную и все критические точки: | ||
| Подробное решение: 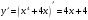 Находим критические точки 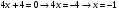 Точка 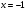 входит в заданный интервал входит в заданный интервал 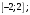 | ||
| 2) Вычислить значения функции в критических точках: | ||
| Подробное решение: Находим значение функции в точке х =-1 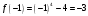 | ||
| 3)Вычислить значения функции на концах промежутка: | ||
| Подробное решение: Находим значение на концах интервала 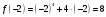 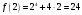 | ||
| 4)Сравнить все полученные значения функции и выбрать среди них самое большое и самое малое: | ||
| Подробное решение: Из полученных значений выбираем наибольшее и наименьшее: 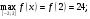 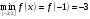 | ||
| 2а. | Провести полное исследование и построить графики данных функций: 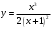 | Построить график, используя полученные результаты |
| Найти область определения функции, исследовать её поведение на границах этой области: | | |
| Подробное решение: Область определения данной функции находим из неравенства 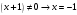 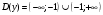 | ||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | ||
| Подробное решение: Функция неопределенна в точке х = -1 Найдем односторонние пределы в этой точке: 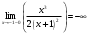 ; ; 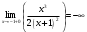 Односторонние пределы равны ∞, значит, функция f(x) терпит разрыв 2-го рода в точке x=-1. | ||
| Исследовать периодичность, чётность (нечётность): | ||
| Подробное решение: Функция непериодичная 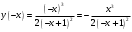 . Функция является не четной и не нечетной,т.е. имеет общий вид. . Функция является не четной и не нечетной,т.е. имеет общий вид. | ||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | ||
| Подробное решение: Точка пересечения с осью Оу: 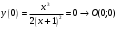 Точка пересечения с осью Ох: 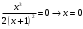 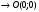 Находим интервалы знакопостоянства 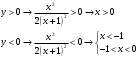 | ||
| Найти асимптоты: | ||
| Подробное решение: Функция f(x) терпит разрыв 2-го рода в точке x=-1. Следовательно, х = -1 является вертикальной асимптотой. Горизонтальные асимптоты Для поиска горизонтальных асимптот, вычисляем пределы функции на бесконечности. 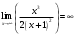 Следовательно, горизонтальной асимптоты нет. Для отыскания наклонной асимптоты при 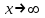 вычислим следующие два предела вычислим следующие два предела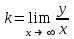 , , 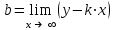 . Если оба они существуют и конечны, то прямая . Если оба они существуют и конечны, то прямая 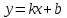 , является наклонной асимптотой при , является наклонной асимптотой при 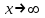 графика функции графика функции 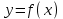 . .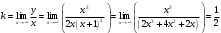 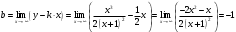 , ,Следовательно, график имеет наклонную асимптоту 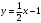 . . | ||
| Найти точки экстремума и интервалы монотонности: | ||
| Подробное решение: Находим первую производную 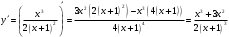 Решая уравнение 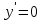 , получим: , получим: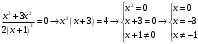 , ,Критические точки и точка разрыва разбивают область определения функции на части. Определим знак производной в каждой из них. Получим: 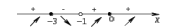 Следовательно, функция возрастает на интервале 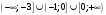 , функция убывает на интервале , функция убывает на интервале 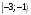 . .Точка 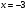 – точка максимума. – точка максимума. 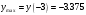 . . 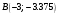 Точки минимума нет | ||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | ||
| Подробное решение: Найдем вторую производную функции и критические точки второго рода. Имеем: 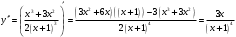 Решая уравнение 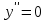 , получим: , получим: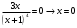 Точка разрыва и критическая точка разбивает область определения функции на части. Определим знак производной в каждой из них. 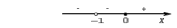 Следовательно, график функции вогнутый на интервале 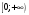 и график функции выпуклый на интервале и график функции выпуклый на интервале 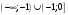 . .Точка перегиба х = 0, тогда у = 0 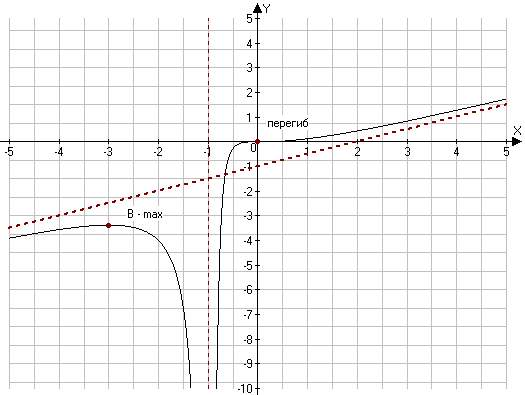 | ||
| 2б. | Провести полное исследование и построить графики данных функций: 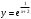 | Построить график, используя полученные результаты |
| Найти область определения функции, исследовать её поведение на границах этой области: | | |
| Подробное решение: Область определения данной функции находим из неравенства 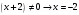 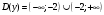 | ||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | ||
| Подробное решение: Функция неопределенна в точке х = -2 Найдем односторонние пределы в этой точке: 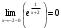 ; ; 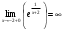 Односторонние пределы равны ∞, значит, функция f(x) терпит разрыв 2-го рода в точке x=-2. | ||
| Исследовать периодичность, чётность (нечётность): | ||
| Подробное решение: Функция непериодичная 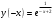 . Функция является не четной и не нечетной,т.е. имеет общий вид. . Функция является не четной и не нечетной,т.е. имеет общий вид. | ||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | ||
| Подробное решение: Точка пересечения с осью Оу: 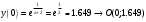 Точка пересечения с осью Ох: 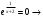 точек пересечения нет точек пересечения нетНаходим интервалы знакопостоянства 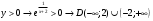 | ||
| Найти асимптоты: | ||
| Подробное решение: Функция f(x) терпит разрыв 2-го рода в точке x=-2. Следовательно, х = -2 является вертикальной асимптотой. Горизонтальные асимптоты Для поиска горизонтальных асимптот, вычисляем пределы функции на бесконечности. 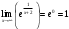 Следовательно, горизонтальная асимптота у=1. Для отыскания наклонной асимптоты при 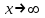 вычислим следующие два предела вычислим следующие два предела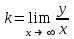 , , 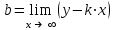 . Если оба они существуют и конечны, то прямая . Если оба они существуют и конечны, то прямая 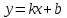 , является наклонной асимптотой при , является наклонной асимптотой при 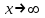 графика функции графика функции 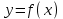 . .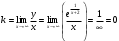 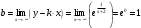 , ,Следовательно, график имеет наклонную асимптоту равную горизонтальной 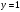 . . | ||
| Найти точки экстремума и интервалы монотонности: | ||
| Подробное решение: Находим первую производную 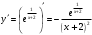 Решая уравнение 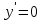 , получим: , получим: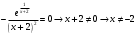 , ,Критические точки и точка разрыва разбивают область определения функции на части. Определим знак производной в каждой из них. Получим:  Следовательно, функция убывает на всей области определения. Точек экстремума нет | ||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | ||
| Подробное решение: Найдем вторую производную функции и критические точки второго рода. Имеем: 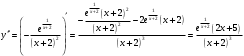 Решая уравнение 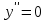 , получим: , получим: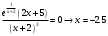 Точка разрыва и критическая точка разбивает область определения функции на части. Определим знак производной в каждой из них. 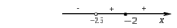 Следовательно, график функции вогнутый на интервале 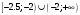 и график функции выпуклый на интервале и график функции выпуклый на интервале 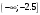 . .Точка перегиба х = -2.5, тогда у = 0.135 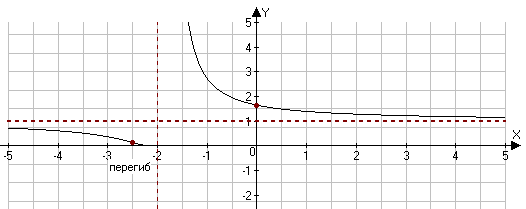 |