Файл: Контрольная работа по предмету инновационные и перспективные технологии транспорта углеводородов раздел.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 191
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МиНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«тюменский государственный нефтегазовый университет»
Институт Транспорта
Кафедра «Транспорт углеводородных ресурсов»
Контрольная работа
по предмету
ИННОВАЦИОННЫЕ И ПЕРСПЕКТИВНЫЕ ТЕХНОЛОГИИ ТРАНСПОРТА УГЛЕВОДОРОДОВ
раздел
Основные физические свойства нефти и газа,
Основные объекты магистрального транспорта нефти и газа
| Выполнил: Васютков Е.Н. | Проверил: |
| Студент группы: | д.т.н., профессор |
| Вариант: 4 | Земенков Ю.Д |
| Номер зачетной книжки: | |
Тюмень
ТюмГНГУ
2016
Задача 1.1.
Молярная масса газа равна М. Определить его плотность при t °С и абсолютном давлении р.
| № вар. | М | t, °С | р, Па |
| 4. | 18 | 215 | 9,51 104 |
Решение:
Плотность газа при 0 °С и 1 атм может быть определена по его молярной массе М.
ρ =
где 22,41 м3 – объем одного моля любого газа при 0 °С и 1 атм.
Пересчет плотности с одних параметров состояния на другие можно произвести по формуле:
где p1 и p2 – абсолютные давления газа; T1 и T2 – абсолютные температуры газа; z1 и z2 – коэффициенты сжимаемости газа, для идеального газа принимаем, z = 1.
Ответ: ρ2 = 0,422 кг/м3.
Задача 1.2.
Определить абсолютную плотность газовой смеси при следующем объемном составе: А % метана, В % этана и С % пропана при стандартных условиях и относительную плотность смеси по воздуху.
Молярные массы: Плотности при 20С и 1 атм:
метан 16,043 0,717
этан 30,07 1,344
пропан 44,097 1,967
воздух 28,96 1,206
-
№ вар.
А
В
С
4.
73
17
10
Решение:
Плотность газовой смеси определяется по правилу смешения:
где а1, а2, а3, аn – объемные концентрации компонентов смеси;
1, 2, 3, n – плотности компонентов смеси.
Относительная плотность газа:
где ρв = 1,206 кг/м3 – плотность воздуха.
Плотность газовой смеси можно определить и по молярной массе:
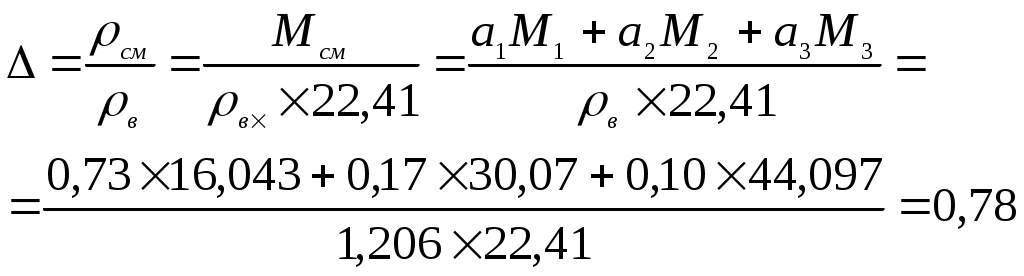
Ответ: Δ = 0,78.
Задача 1.3.
Газ относительной плотностью 0,75 при температуре t С и давлении p МПа занимает объем V м3. Определить его объем для стандартных условий и при 20С и атмосферном давлении. Коэффициент сжимаемости принять равным 0,95.
| № вар. | V, м3 | t, °С | р, МПа |
| 4. | 280 | 55 | 1,5 |
Решение:
Абсолютное давление газа:
Па.
Абсолютная температура газа:
Приведение объема газа к нужным параметрам выполняется по следующей зависимости:
Тогда объем для стандартных условий (T2 = 273,15 (0 °С) и p2 = 1 атм = 101325 Па)
Объем при 20 °С (T2 = 273,15 + 20 = 293,15 К) и атмосферном давлении
Ответ: V0= 3811,49 м3; V20= 4090,56 м3.
Задача 1.4.
62 кг жидкого газа имеет массовый состав: А % пропана, В % бутана, С % пентана. Определить объем газа после его испарения при 0С и атмосферном давлении.
Молярные массы:
пропан 44,097
бутан 58,124
пентан 72,151
| № вар. | А | В | С |
| 4. | 73 | 17 | 10 |
Решение:
Если известен массовый состав газовой смеси в процентах, то его средняя молярная масса может быть определена по формуле:
где q1, q2, q3, qn – массовый состав компонентов смеси в процентах.
Объем газа после испарения:
где 22,41 – объем одного киломоля лютого газа при 0° и атмосферном давлении, м3.
Ответ: V = 28,99 м3.
Задача 1.5.
В вертикальном цилиндрическом резервуаре диаметром d хранится m тонн нефти, плотность которой при 0°С составляет 0. Определить колебание уровня в резервуаре при колебании температуры нефти от 0°С до t. Расширение резервуара не учитывать. Коэффициент теплового расширения нефти принять равным Т = 0,00072 1/град.
| № вар. | d, м | 0, кг/м3 | t, °С | m, т |
| 4 | 4 | 835 | 29 | 97 |
Решение:
Объем нефти в резервуаре:
Увеличение объема нефти при повышении температуры на Δt = t2 – t1:
Колебание уровня нефти в резервуаре:
Ответ: Δh = 193 мм.
Задача 1.6.
Винтовой пресс Рухгольца (рис. 1) для тарировки пружинных манометров работает на масле с коэффициентом сжимаемости Р = 0,638 10-9 Па-1. Определить, на сколько оборотов надо повернуть маховик винта, чтобы поднять давление на р Па, если начальный объём рабочей камеры пресса составляет V, диаметр плунжера d, шаг винта h. Стенки рабочей камеры считать недеформируемыми.
| № вар. | р, Па | V, м3 | d, м | h, мм |
| 4 | 9,2 104 | 0,624 10-3 | 0,024 | 2 |
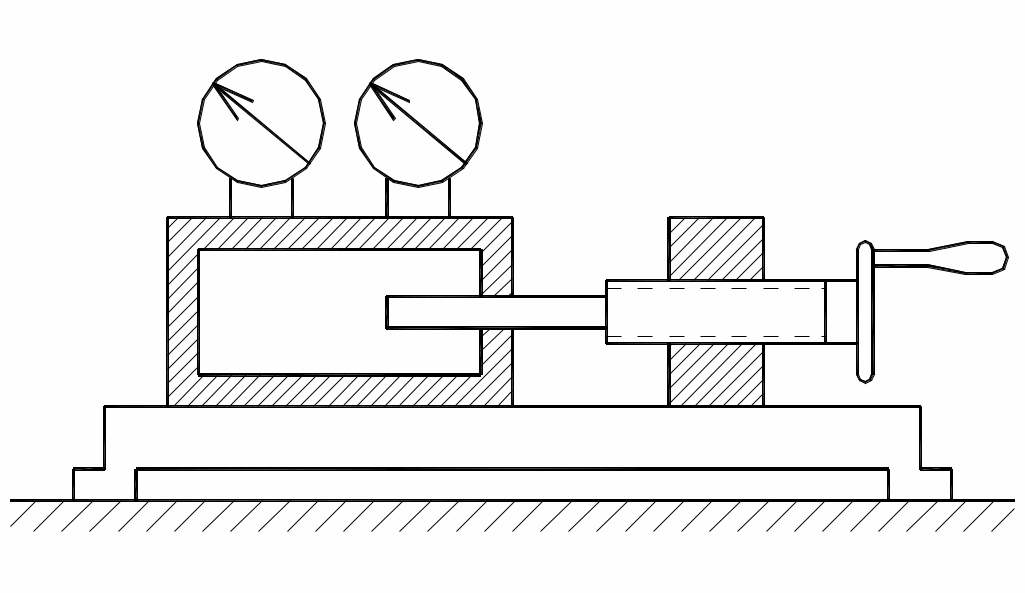
Рис. 1
Решение:
Давление в рабочей камере пресса повышается вследствие уменьшения объема масла при поступательном движении плунжера.
Изменение объема масла ΔV при повышении давления в камере на величину Δp можно найти из выражения для коэффициента объемного сжатия βp.
Длина l, на которую должен продвинуться плунжер, равна:
где S – площадь поперечного сечения плунжера.
При этом маховик винта необходимо повернуть на:
Ответ:
Задача 1.7.
В закрытом резервуаре с нефтью плотностью вакуумметр, установленный на его крышке, показывает РВ Па (рис. 2). Определить показания манометра РМ, присоединённого к резервуару на глубине Н от поверхности жидкости.
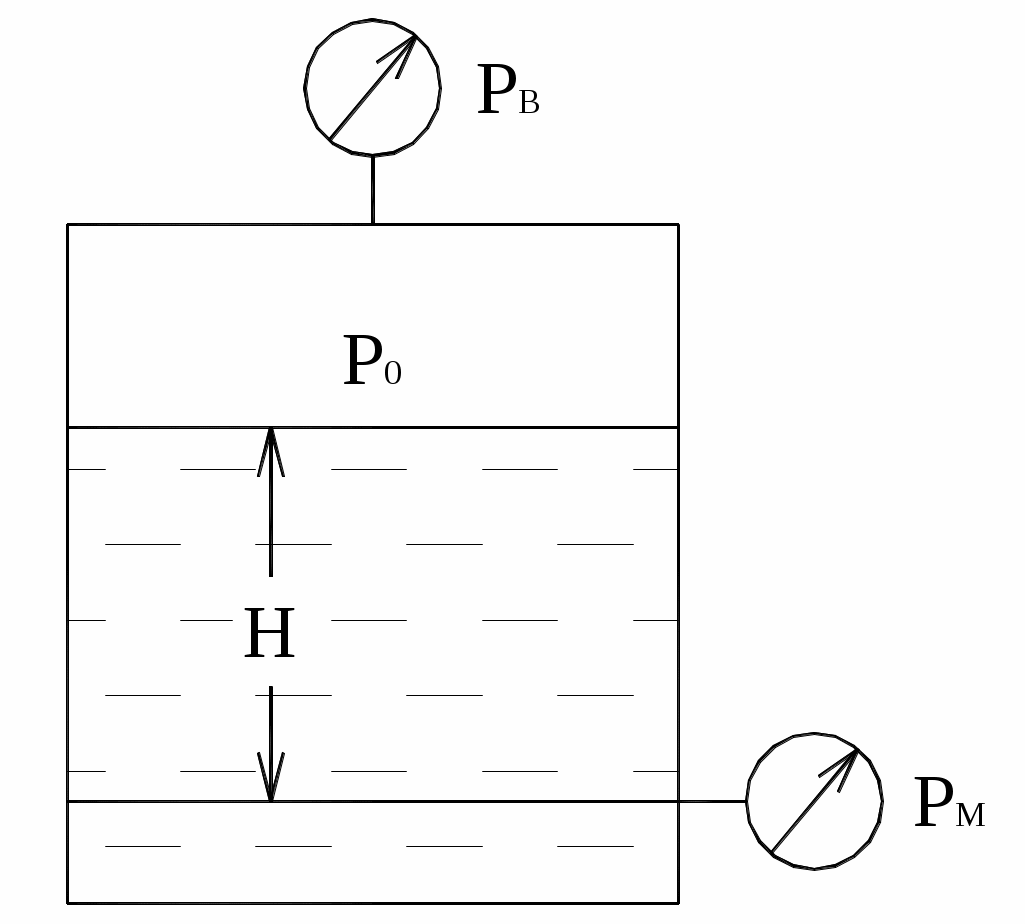
Рис. 2
-
№ вар.
, кг/м3
рв, Па
Н, м
4
855
1,22 104
7
Решение:
Определим давление на свободной поверхности жидкости в закрытом резервуаре. Так как вакуумметр показывает вакуумметрическое давление, то на поверхности жидкости в резервуаре давление тоже будет вакуумметрическое.
Запишем уравнение давления на глубине H от поверхности нефти в резервуаре (в месте установки манометра)
Тогда показание манометра составит:
Ответ:
Задача 1.8.
Найти избыточное давление в сосуде А с водой по показаниям многоступенчатого двух жидкостного ртутного манометра (рис. 3). Высоты столбиков ртути равны соответственно h1, h2, h3, h4, h5. Плотность воды равна . Плотность ртути рт.
| № вар. | h1, см | h2, см | h3, см | h4, см | h5, см | , кг/м3 | рт, кг/м3 |
| 4 | 85 | 42 | 55 | 44 | 100 | 103 | 1,36 103 |
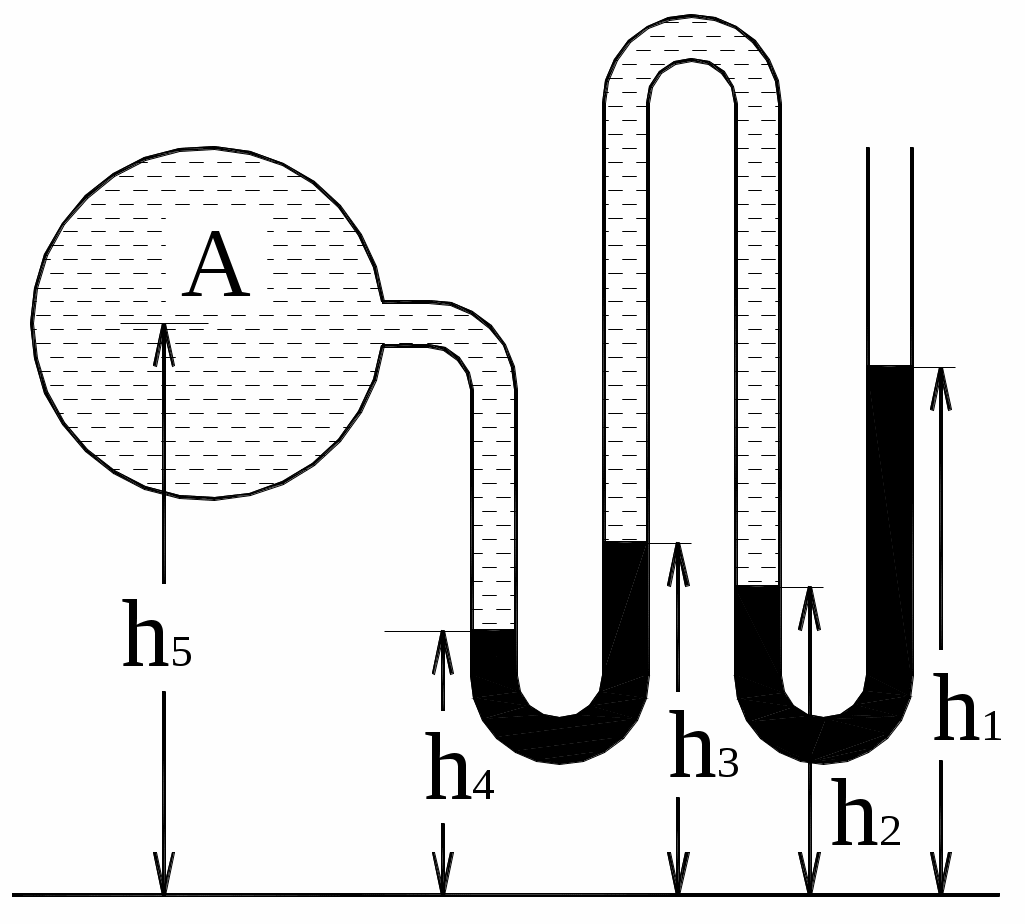
Рис. 3
Решение:
Так как жидкость находится в равновесии, то давления в точке 1 и в точке 2 равны как давления в точках одного и того же объема однородной покоящейся жидкости, расположенных на одной горизонтали, т. е. p1 = p2. На том же основании p3 = p4, p5 = p6. В то же время избыточное давление:
Исключив из этих соотношений промежуточные давления p2, p4, p6, получим:
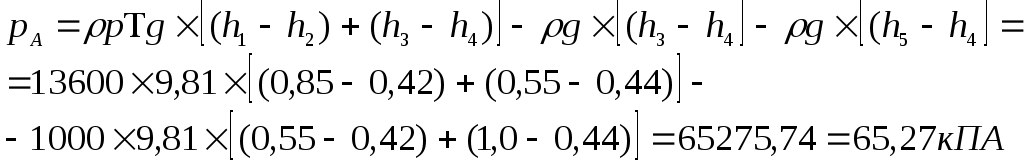
Ответ: pА = 65,27 кПа.
Задача 1.9.
Определить давление на забое закрытой газовой скважины (рис. 4), если глубина скважины Н, манометрическое давление на устье рм, плотность природного газа при атмосферном давлении и температуре в скважине (считаемой неизменной по высоте) , атмосферное давление рА.
| № вар. | Н, м | рм, Па | , кг/м3 | рА, кПа |
| 4 | 215 | 10,9 | 0,73 | 98 |
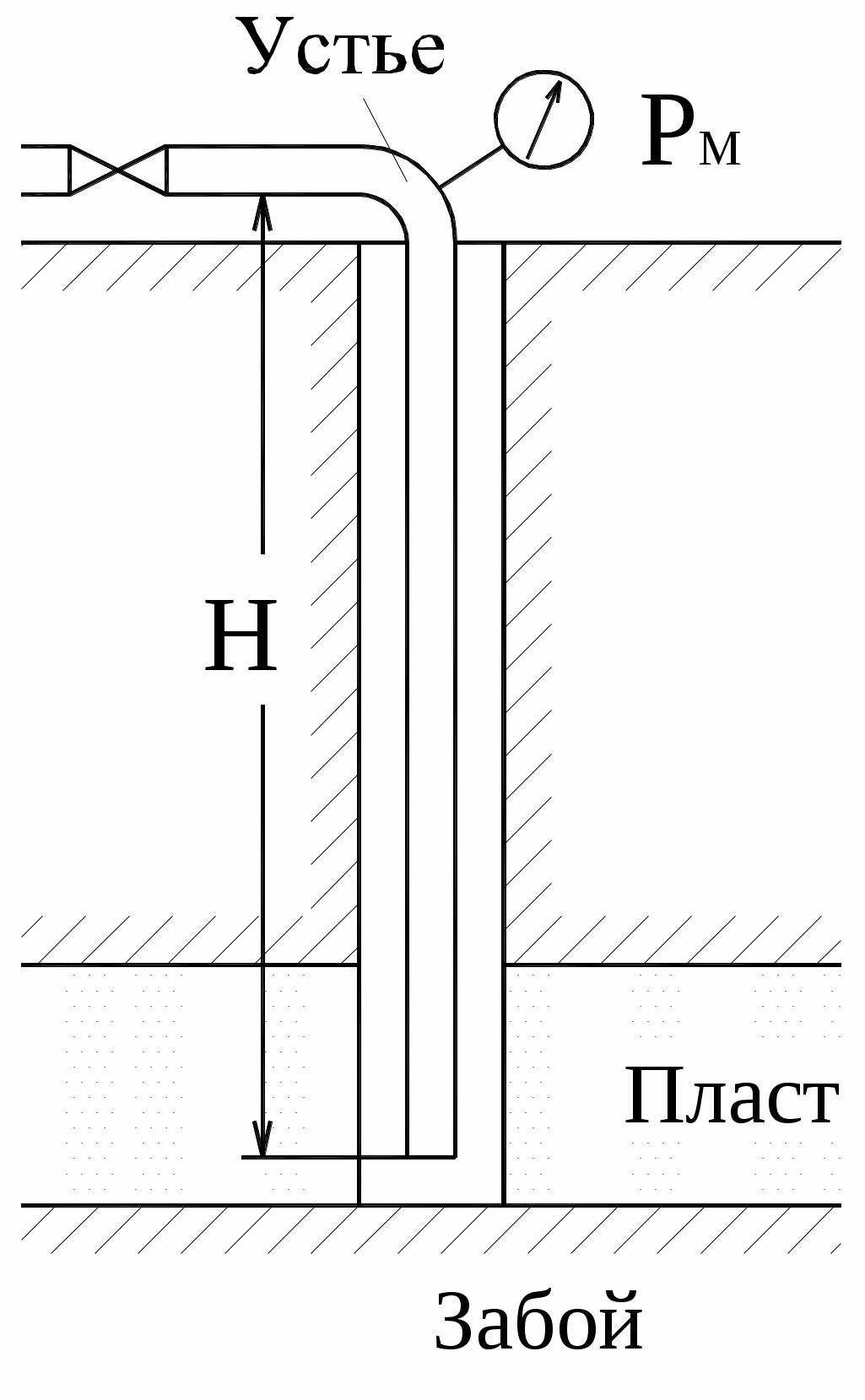
Рис. 4
Решение:
Для определения давления на забое газовой скважины воспользуемся барометрической формулой:
В нашей задаче p0 – абсолютное давление газа на устье скважины
ρ0 – плотность при давлении p0;
Из уравнения состояния газа следует:
а показатель степени:
Тогда
Ответ: p = 99562 Па