1 вариант.

а) Какую фигуру представляет боковая грань призмы?

1) квадрат; 2) параллелограмм; 3) прямоугольник.

б) Какую фигуру представляет боковая грань правильной пирамиды?

1) треугольник; 2) прямоугольный треугольник; 3) равнобедренный треугольник.

в) Какой многоугольник лежит в основании правильной 4-хугольной призмы?

1) квадрат; 2)параллелограмм; 3)прямоугольник.

г) Сколько диагоналей можно провести в 4-хугольной призме?

1) 2; 2) 4; 3) 6.

д) Сколько рёбер у шестиугольной призмы?      

1) 18; 2) 6;   3) 24; 

е) Измерениями прямоугольного параллелепипеда называются:

1) длины трёх произвольно взятых диагоналей;

2) длины трёх равных рёбер параллелепипеда;

3) длины трёх рёбер, имеющих общую вершину;

4) длины диагоналей основания параллелепипеда;

5) длины смежных сторон и диагонали параллелепипеда.


II вариант.

а) Какой многоугольник лежит в боковой грани параллелепипеда?

. 1) квадрат; 2) параллелограмм; 3) прямоугольник

б) Какую фигуру представляет основание правильной треугольной призмы?

1) равносторонний треугольник;

2) равнобедренный треугольник;

3) прямоугольный треугольник.

в) Какую фигуру представляет боковая грань прямой призмы?

1) квадрат; 2)параллелограмм; 3)прямоугольник.

г) Какую фигуру представляют сечения, проходящие через боковые ребра у прямой призмы?

1) квадрат; 2)параллелограмм; 3)прямоугольник.

д) Сколько граней у шестиугольной пирамиды? 

1) 6; 2) 7;   3) 10; 4) 1

е) Апофема- это

1) высота боковой грани пирамиды;

2) высота пирамиды;

3) высота боковой грани правильной пирамиды.
3) Составление кластера по теме «Площади». Проверка знания формул, которые применяются на данном уроке. (время- 5'). Чертежи делают от руки. Оценка- max 5 баллов.

На каждой парте лежат листы. Посередине листа в рамке написать слово «Площадь» и для данного перечня геометрических фигур выполнить следующие задания:

1. 
   нарисовать саму фигуру;
   
2. 
   написать формулу нахождения площади этой фигуры.
   

Геометрические фигуры: прямоугольный треугольник, равносторонний треугольник, любой треугольник, квадрат, прямоугольник, трапеция, круг, площади боковой и полной поверхностей для призмы и пирамиды.

---

Индивидуальная работа для слабых учащихся: игра «Домино».

Sбок. прав.пирамиды

S прям. треугольника

ab

S прямоуг.

с2= а2 + в2

Теорема Пифагора

Sбок. прям. призмы

P*h	S квадрата

а2	S равност.треуг.

а2	S трапеции

*h

P*h

Комментарии по этому этапу. Выводы. Заполнение оценочных листов. ( Время 3')

3. 
   Систематизация и обобщение ранее изученного.
   

Задача этапа: систематизация и обобщение знаний, умений и навыков решения задач по данной теме, проверить умение учащихся применять теоретический материал к решению задач ЕГЭ (I часть)

1. 
   Устное решение задач ЕГЭ по готовым чертежам слайды). Работают в группах.
   

Группы состоят из учащихся 2-х соседних парт. Комментируют решения. (Время-10') .

Задачи для I группы (для IV группы):

№1. Найдите квадрат расстояния между вершинами 

---

D и C₂многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.



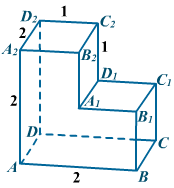
№2. Найдите угол C₁BC прямоугольного параллелепипеда, для которого AB = 5 , AD = 4,  AA₁ = 4. Ответ дайте в градусах.

Задания для II группы (для Vгруппы):

№1. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.

№2.В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите уголAC₁C. Ответ дайте в градусах.

Задания для III группы (для VI группы):

№1.В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками B и E.

№2. В правильной четырехугольной пирамиде SABCD точка O - центр основания, S -вершина, 
SO = 4, SC = 5. Найдите длину отрезка AC.  
2) Практическая работа. ( Время-25').


Задача этапа: применение знаний, умений и навыков решения задач по данной теме для более сложных задач.

Учащиеся работают по группам. На столах лежат карточки с разным уровнем задач (зелёный цвет-I уровень (задания ЕГЭ- более сложные), синий цвет- II уровень, красный цвет- III уровень). С каждой группы по одному члену команды подходят к учителю и объясняют решение задачи. Можно организовать объяснение для всего класса.

I уровень. (Карточки зелёного цвета.)

Карточка №1.

Найти площадь поверхности данной фигуры.



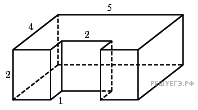
Карточка №2.

Если каж­дое ребро куба уве­ли­чить на 1, то его пло­щадь по­верх­но­сти уве­ли­чит­ся на 54. Най­ди­те ребро куба.



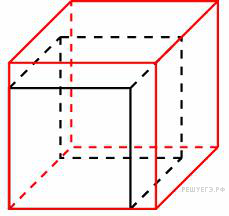
Карточка №3.

Во сколь­ко раз уве­ли­чит­ся пло­щадь по­верх­но­сти ок­та­эд­ра, если все его ребра уве­ли­чить в 3 раза?

---

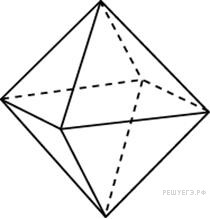
II уровень. (Карточки синего цвета.)

Карточка №1.

Основание прямого параллелепипеда - ромб. Найдите площадь боковой поверхности параллелепипеда, если площади его диагональных сечений Р и Q.

Карточка №2.

Диагональное сечение правильной четырехугольной призмы имеет площадь Q. Найдите площадь боковой поверхности призмы.
Карточка №3.

В прямой призме АВСА1В1С1 АВ = 13, ВС = 21, АС = 20. Диагональ боковой грани А1С составляет с плоскостью грани СС₁В₁В угол 30°. Найдите площадь полной поверхности призмы.

III уровень.(Карточки красного цвета).

Карточка №1.

Основание пирамиды - прямоугольный треугольник с катетом 4√3 см и противолежащим углом 60°. Все боковые ребра пирамиды наклонены к плоскости основания под углом 45°. Найдите площадь боковой поверхности пирамиды.

Карточка №2.

Основание пирамиды - прямоугольный треугольник с острым углом 30°. Высота пирамиды равна 4 см и образует со всеми боковыми ребрами углы 45°. Найдите площадь боковой поверхности пирамиды.

Карточка №3.

В правильной треугольной пирамиде сторона основания равна m. Угол между смежными боковыми гранями равен 120°. Найдите площадь боковой поверхности пирамиды.

4. 
   Самостоятельная работа.
   

Задача этапа: проверить уровень сформированности знаний, умений и навыков решения задач по теме «Многогранники».

Работают по вариантам. Задания -3-х уровневая. Учитель проводит инструктаж. Оценка: за 1 задачу-«3», за 2 задачи- «4», за все правильно решенные задания –«5». Оценки выставляются отдельно, после проверки решений учителем. В конце урока учащиеся проверяют только полученные ответы.

I вариант.

1. 
   Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы.
   
2. 
   Основание прямой призмы - прямоугольный треугольник с катетами 15 и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.
   
3. 
   Основанием пирамиды является треугольник со сторонами 12 см, 10 см, 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь полной поверхности пирамиды.
   

---

II вариант.

1. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы.

2. Основание прямой призмы - прямоугольный треугольник с гипотенузой 25 см и катетом 20 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.  

3. Основанием пирамиды является треугольник со сторонами 10 см, 8 см, 6 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь полной поверхности пирамиды.

Ответы:

I вариант.

№1- S_бок.= 144, S_полн.= 18( 8+ ).

№2- S_бок.= 360, S_полн.= 660.

№3- S_полн.= 48(1+ )
II вариант.

№1- S_бок.= 324, S_полн.=36(9+2 ).
№2- S_бок.= 600, S_полн.= 900.
№3- S_бок.= S_полн.=24(1+ ) .

5. 
   Домашнее задание.
   

№1.Задача.

Сколько штук досок размером 100 мм на 2500 мм потребуется на обшивку крыши и потолка сарая, если длина крыши 4 м, ширина 3 м, а высота 2 м? Крыша имеет форму прямой треугольной призмы, в основании которой равнобедренный треугольник.

№2. Задачи самостоятельной работы (меняются вариантами).

№3. Теоретический материал- повторить.

5. 
   Рефлексия.
   

1. 
   Выставление оценок из оценочного листа.
   
2. 
   Обсуждение урока.
   

• 
  Понравился / не понравился урок?
  
• 
  Что интересного было на уроке?
  
• 
  Чем вам запомнится этот урок?
  
• 
  На уроке для меня было важно…
  
• 
  На уроке мне было сложно…
  
• 
  На уроке я понял (а)…
  
• 
  Теперь я умею…
  
• 
  Довольны ли вы своей работой на уроке?
  

Приложение.

Кроссворд.
По горизонтали:

1)Элемент многогранника.

2)Перпендикуляр, опущенный из вершины пирамиды на основание.

3)Призма, у которой боковое ребро перпендикулярно к основанию.

4)Многогранник,  две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани —

---

Смотрите также файлы

• Организация неонатологической службы.pdf

• Глагольные счетные слова в китайском языке оглавление введение исследования понятия счетные слова.docx

• Физическое воспитание детей старшего школьного возраста.docx

• 1. Преодоление дипломатической изоляции.docx

• Административная ответственность юридических лиц.docx