Лабораторная работа 7. Синтез систем управления средствами MATLAB SISO Design Tool.

(на основе материалов раздела 5.7 учебного пособия Рогачев Г.Н. Программные средства MATLAB для моделирования, анализа и синтеза систем управления/ Г.Н. Рогачев. – Самара: Самар. гос. техн. ун-т, 2019. – 183 с.)

5.7. Синтез систем управления в CST MATLAB

5.7.1. SISO Design Tool и его использование для решения задач синтеза САУ

Пакет Control System Toolbox позволяет проектировать линейные системы автоматического управления. Причем проектирование, как и анализ, может осуществляться либо через командную строку, либо в графическом интерфейсе пользователя, SISO Design Tool. Однако, как явствует из названия, в графическом интерфейсе пользователя можно синтезировать лишь системы с одним входом и одним выходом (SISO – Single Input/Single Output). Имеется несколько способов проектировать контуры управления с обратной связью, используя SISO Design Tool. Первая группа методов относится к классическим. Здесь можно указать метод корневого годографа (функция rlocus или SISO Design Tool), метод ЛАФЧХ (SISO Design Tool). Вторая группа предоставляемых SISO Design Tool методов –средства автоматической настройки регуляторов (Automated Tuning Design) – методы современной теории управления на базе оптимизационных подходов и инженерные методы настройки ПИД-регуляторов.

5.7.2. Метод корневого годографа¹

Многие важные свойства системы (например, быстродействие, перерегулирование) определяются расположением корней характеристического уравнения на комплексной плоскости. Простейший способ обеспечить в замкнутой системе требуемые показатели качества – применить П-регулятор (усилитель с коэффициентом ), который изменяет коэффициент усиления разомкнутой системы и расположение корней характеристического уравнения. При изменении от 0 до корни описывают кривые

---

, которые называются корневым годографом.

Для синтеза регулятора может использоваться графический интерфейс пользователя SISO Design Tool. Его запуск осуществляется командой sisotool. Далее для отображения редактора Root Locus Editor в меню View необходимо выбрать пункт Root Locus (корневой годограф) (рис. 5.16).

С помощью SISO Design Tool можно выбирать нужное расположение корней (и соответствующий коэффициент усиления), «перетаскивая» их мышкой. Заметим, что при перемещении одного корня смещаются и все остальные, поскольку система имеет одну степень свободы – изменяющийся коэффициент усиления контура.

Корни при выбранном коэффициенте усиления изображаются фиолетовыми квадратами. Концы годографа для каждого корня помечены крестиком ( ) и кружком ( ). Сетка (для ее вывода надо выбрать в контекстном меню пункт Grid) показывает линии равных показателей колебательности (коэффициента демпфирования, damping factor) – прямые, выходящие из начала координат, и линии равных собственных частот (natural frequency) – окружности с центром в начале координат.

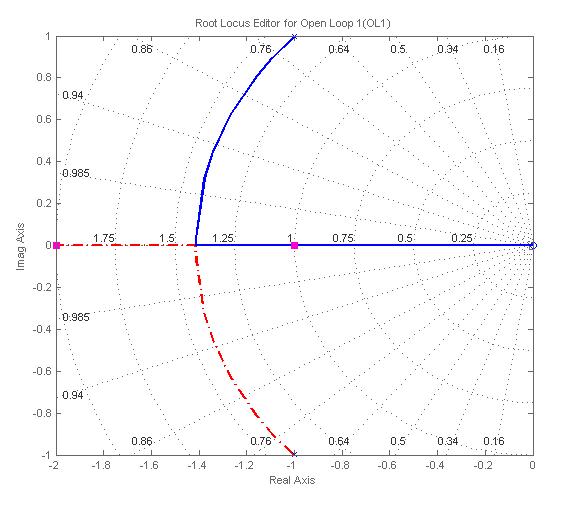
Рис. 5.16. Корневой годограф системы с объектом управления и П-регулятором

В контекстном меню можно установить ограничения на расположение полюсов так, чтобы перерегулирование и время переходного процесса не превышали заданных. Для этого надо выбрать пункт Design Constraints – New и выбрать в выпадающем списке Percent Overshoot (перерегулирование в процентах) и Settling Time (время переходного процесса как время попадания в 2%-ную зону).

Ограничения показываются в виде границ запрещенных зон. При использовании двух ограничений (первое – на время переходного процесса, второе – на перерегулирование) область допустимого расположения корней представляет собой усеченный сектор в левой части рис. 5.17. Если перетаскиванием корней (то есть изменением усиления контура) не удается расположить корни в этой области

---

, необходимо усложнять передаточную функцию регулятора, добавляя нули и полюса (контекстное меню Add Pole/Zero или меню Edit Compensator).


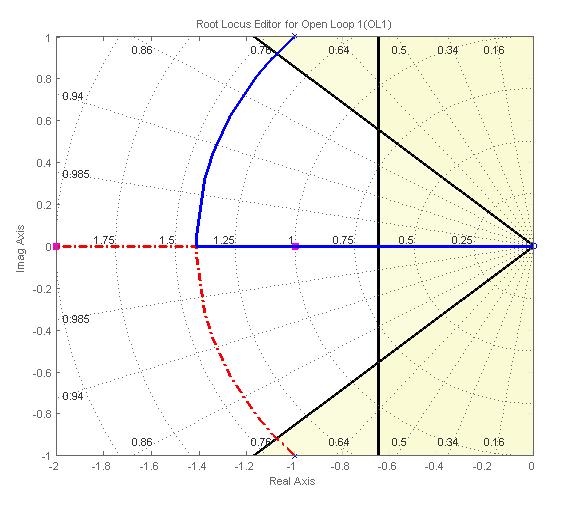
Рис. 5.17. Корневой годограф системы с ограничениями

в виде границ запрещенных зон
5.7.3. Синтез с помощью ЛАФЧХ

Еще один метод синтеза регуляторов в графическом интерфейсе пользователя SISO Design Tool – синтез с помощью логарифмических амплитудно-фазовых частотных характеристик (ЛАФЧХ) разомкнутой системы (диаграмм Боде по зарубежной терминологии).

Пусть разомкнутая система имеет передаточную функцию . ЛАФЧХ включает в себя две кривые – амплитудную частотную характеристику (ЛАЧХ) и фазовую (ЛФЧХ) . Низкочастотная часть ЛАЧХ определяет точность системы, среднечастотная (вблизи частоты среза ) – устойчивость и качество переходного процесса, высокочастотная – чувствительность к помехам.

Если система содержит интегратор, низкочастотная часть имеет ненулевой наклон (-20 дБ/дек) и постоянный сигнал отслеживается без установившейся ошибки. У системы с двумя интеграторами ЛАЧХ имеет в области низких частот наклон –40 дБ/дек, без установившейся ошибки отслеживается не только постоянный, но и линейно возрастающий сигнал.

Запас устойчивости по амплитуде (в дБ) – это расстояние от ЛАЧХ до горизонтальной прямой дБ на частоте, на которой фазовая характеристика пересекает прямую . На этой частоте система должна иметь коэффициент усиления меньше 1 (или ). Запас устойчивости по амплитуде показывает, насколько можно увеличить общее усиление замкнутого контура, чтобы не потерять устойчивость системы. Например, при запасе 10 дБ (или примерно 3.16 в абсолютных единицах) можно увеличить коэффициент усиления в 3.16 раза. Запас устойчивости по фазе

---

(в градусах) – это расстояние от частотной характеристики до горизонтальной прямой на частоте среза . На этой частоте фазовая характеристика должна иметь значение больше, чем . Запас устойчивости по фазе – это наибольшая дополнительная задержка сигнала по фазе, которая не приводит к потере устойчивости. Допустимым считается запас по амплитуде не менее 6 дБ и запас по фазе не менее 30 градусов (рис. 5.18).


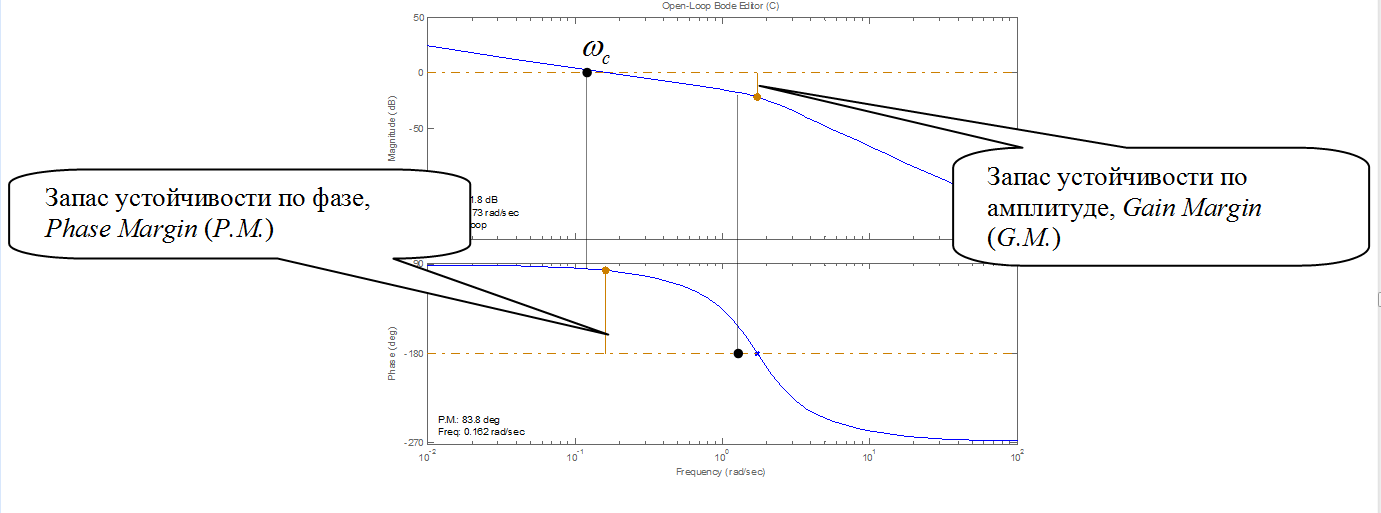
Рис. 5.18. ЛАФЧХ системы с интегратором
Более сложные требования к качеству работы САУ приводят к тому, что ЛАЧХ разомкнутой системы не должна заходить в некоторые запретные области. Обычно требуется, чтобы система имела высокую точность (большой коэффициент усиления по контуру) для низких частот и подавляла высокочастотные помехи (имела низкое усиление в области высоких частот). Частота среза выбирается исходя из требований к быстродействию. Для обеспечения хорошего качества переходных процессов рекомендуется, чтобы ЛАЧХ пересекала ось с наклоном –20 дБ/дек. Это объясняется тем, что наклон –20 дБ/дек, соответствующий апериодическому звену, приводит к наименьшей колебательности переходного процесса. Точки перехода (излома асимптотической ЛАЧХ) от низкочастотной части к среднечастотной и далее к высокочастотной должны отстоять от оси на 12-16 дБ. Таким образом, типичная ЛАЧХ имеет вид, показанный на рис. 5.19. Серым цветом показаны запретные области, которые определяются требованиями к точности и подавлению помех.

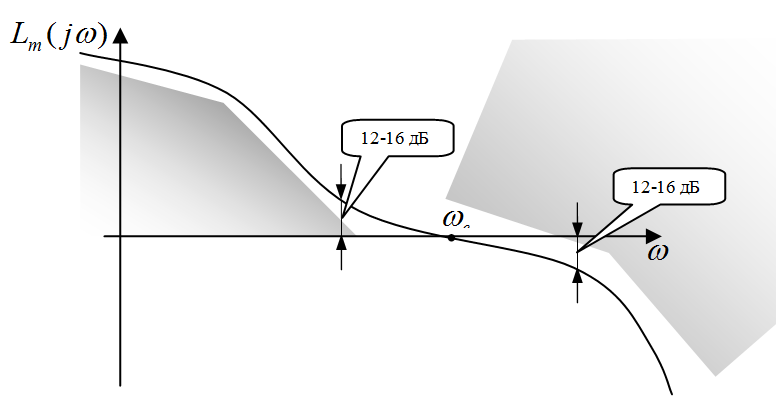
Рис. 5.19. Типичная желаемая ЛАФЧХ системы
Простейший вариант корректирующего звена – П-регулятор, который изменяет коэффициент усиления разомкнутой системы и расположение ЛАЧХ. При увеличении коэффициента усиления П‑регулятора, а значит и контура в целом, происходит «подъем» ЛАЧХ, фазовая характеристика не изменяется. Точность системы (при отработке низкочастотных сигналов) повышается, однако увеличивается и влияние высокочастотных помех. Поскольку частота среза увеличивается, повышается быстродействие системы. При этом переходные процессы приобретают выраженный колебательный характер, запасы устойчивости уменьшаются, при дальнейшем увеличении коэффициента усиления теряется устойчивость.

---

Если изменением усиления контура не удается расположить корни в этой области, необходимо усложнять передаточную функцию регулятора, добавляя нули и полюса (контекстное меню Add Pole/Zero или меню Edit Compensator).
Задания.

В лабораторной работе №5 рассмотрена система, состоящая из объекта управления, заданного передаточной функцией (ПФ) , датчика обратной связи и регулятора . Передаточные функции объекта управления и датчика обратной связи представлены в таблице.



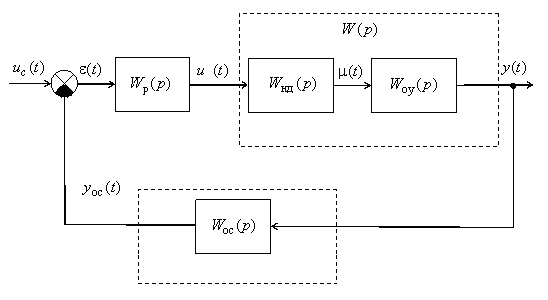
1. Осуществить, используя метод корневого годографа, средствами MATLAB SISO Design Tool синтез П-регулятора. Необходимо, чтобы показатели качества замкнутой системы не превышали заданных значений: статическая ошибка - 5%, перерегулирование - 15% и время переходного процесса 3 с.

2. При невозможности обеспечить заданные значения показателей качества замкнутой системы усложнять передаточную функцию регулятора, добавляя нули и полюса.

3. В графическом инструментарии LTI Viewer исследовать временные и частотные свойства системы с синтезированным регулятором.

4. Повторить задания 1-3 средствами MATLAB SISO Design Tool, используя метод ЛАЧХ.

5. Сравнить результаты. Сделать выводы.
Таблица. Передаточные функции объекта управления и датчика обратной связи

№ вар.
1	2 ---------------------------------------------------------- s^5 + 86 s^4 + 3126 s^3 + 65176 s^2 + 777045 s + 3.619e006	10 ----------- 0.2 p + 1
2	1 ---------------------------------------------------------- s^5 + 68 s^4 + 1958 s^3 + 32300 s^2 + 303973 s + 1.121e006	4 ----------- 0.4 p + 1
3	9 ----------------------------------------------------- s^5 + 47 s^4 + 956 s^3 + 11708 s^2 + 83323 s + 217165	0.8 ------------- 0.25 p + 1
4	3 ------------------------------------------------------- s^5 + 53 s^4 + 1232 s^3 + 18080 s^2 + 156100 s + 452500	1 ----------- 0.6 p + 1
5	8 ------------------------------------------------------- s^5 + 64 s^4 + 1722 s^3 + 25928 s^2 + 219321 s + 747464	25 ----------- 0.3 p + 1
6	6 ---------------------------------------------------------- s^5 + 77 s^4 + 2508 s^3 + 46832 s^2 + 499532 s + 2.085e006	100 ------------ 0.15 p + 1
7	10 --------------------------------------------------- s^5 + 37 s^4 + 620 s^3 + 7020 s^2 + 46539 s + 90423	1 ------------ 0.5 p + 1
8	6 ------------------------------------------------------- s^5 + 54 s^4 + 1318 s^3 + 22288 s^2 + 221544 s + 601120	0.1 ----------- 0.1 p + 1
9	1 ------------------------------------------------------- s^5 + 53 s^4 + 1308 s^3 + 24380 s^2 + 261083 s + 595095	2.5 --------- p + 1
10	10 ---------------------------------------------------------- s^5 + 84 s^4 + 2974 s^3 + 59836 s^2 + 684480 s + 3.095e006	1 ----------- 0.1 p + 1
11	5 ---------------------------------------------------------- s^5 + 80 s^4 + 2622 s^3 + 44972 s^2 + 408125 s + 1.542e006	2.5
12	4 ----------------------------------------------------- s^5 + 41 s^4 + 768 s^3 + 10064 s^2 + 76991 s + 158055	5 --------- p + 1
13	10 ---------------------------------------------------------- s^5 + 76 s^4 + 2406 s^3 + 41676 s^2 + 399040 s + 1.569e006	15
14	2 ----------------------------------------------------- s^5 + 44 s^4 + 858 s^3 + 10768 s^2 + 79449 s + 190180	2 ----------- 0.5 p + 1

---

Смотрите также файлы

• 1. В какой части света находится твоя страна.docx

• Курсовая работа по профессиональному модулю пм. 04 Составление и использование бухгалтерской отчетности.pdf

• Вид работы Курсовая работа Название дисциплины Право социального обеспечения (спо 400201) Тема Предмет права социального обеспечения как отрасли и научной дисциплины Фамилия студента Иванов.doc

• Методы увеличения производительности скважин.docx

• Анализ развития банковских технологий в России.docx