Файл: Лабораторная работа по дисциплине Информационные технологии Студент гр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 56
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерных систем в управлении и проектировании
(КСУП)
МОДЕЛИРОВАНИЕ И ОБРАБОТКА НАУЧНЫХ ДАННЫХ
Лабораторная работа по дисциплине
«Информационные технологии»
| | Выполнил: Студент гр (подпись) И. О. Фамилия «___»__________2022__г. (дата) |
| | Проверил: ______________________________ (должность, ученая степень, звание) ______________ /____________________/ (подпись) И. О. Фамилия «____»_______________20____г. (дата) |
Томск 2022 г.
Цель лабораторной работы: научиться методам математического моделирования и анализа научных данных, а также построению графиков в табличном процессоре Excel и системе MathCAD.
Задания
-
Операции в ЭТ Excel
Моделирование процесса АФ=f(Т, В, Д)
1. На листе 1 подготовьте таблицу в следующем порядке:
1.1 Для диапазона клеток B3:G6 задайте численный формат с 2-мя деся-
тичными знаками.
1.2 В строке 1 разместите заголовок «Моделирование» и сцентруйте его
в пределах A-G. Сохраните файл в рабочей папке c:\temp\kt или «C:\Do-
cuments and Settings\studentst\My Documents\kt» под именем labkt2-1.
1.3 Введите следующие данные:
| | A | B | C |
| 1 | Моделирование | | |
| 2 | | январь | |
| 3 | Т | -10 | =b3+4 |
| 4 | В | 60 | =b4+5 |
| 5 | Д | 0,97 | =b5-0.03 |
| 6 | АФ | =b4/b3*b5 | |
1.4 Данные клеток В2, С3, С4, С5, В6 логически скопируйте до кл.G6.
2. Полученные в зоне А2:G6 табличные данные отобразите встроенным ли-
нейным графиком. Функцию АФ сгладить, выделить цветом и толщиной
линии, включить сетку.
3. Листу 1 присвойте имя «Модель». Сохраните.
4. Скопируйте полученную таблицу на Лист 2. Постройте график в соответ-
ствии с п. 2. Меняя величины параметров Т, В, Д в колонке Е, добейтесь
уменьшения значения функции АФ в ее¨ отображении на графике. Листу 2
присвойте имя «Анализ». Сохраните.
Регрессионный анализ зависимости R=f(t)
1) Откройте лист 3 и для колонок А и В задайте числовой формат с двумя
десятичными знаками.
2) Задайте данные:
| | A | B |
| 1 | t | R |
| 2 | 20,0 | 86,70 |
| 3 | 24,8 | 88,03 |
| 4 | 30,2 | 90,32 |
| 5 | 35,0 | 91,15 |
| 6 | 40,1 | 93,26 |
| 7 | 44,9 | 94,90 |
| 8 | 50,0 | 96,33 |
3) Постройте встроенный точечный график функции R = f (t), где ось Y —
Сопротивление, ось X — Температура, начало координат по оси = 20.
4) Выделите данные на графике и постройте линейную регрессию (пункт
Диаграмма/Добавить линию тренда).
5) Выполните регрессионный анализ (пункт Сервис/Анализ данных/Регрес-
сия), указав для входных данных по Y — B2:В8, по X — A2:A8 и выход-
ных — А24.
6) В отдельные ячейки текущего листа ниже графика скопируйте получен-
ные значения коэффициента корреляции и коэффициентов a ,b зависимости
R(t) = a ⋅ t + b.
7) Сохраните лист с наименованием «Регрессия».
8) Сохраните файл.
II. Операции в системе MathCAD
Моделирование на основе системы рекуррентных уравнений (модель эпидемии)
1) Задайте интервал времени t:=0..20.
2) Для переменных i-инфекция, s-восприимчивость, r-выздоравливаемость задайте векторы начальных условий и перекрестных итераций (строк — 3, колонок — 1):
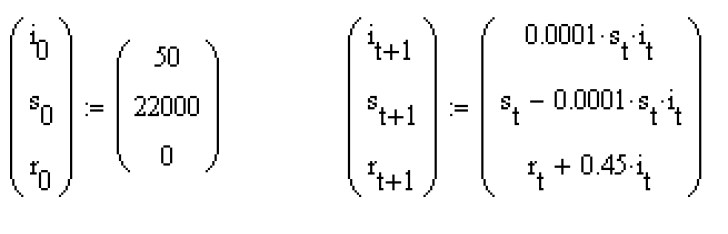
3) Постройте графики зависимостей it, st, rt от t.
4) Скопируйте данные из п.2, 3. Проведите изменения: для i — 20, в формуле
для st+1 коэффициент 0.0001 измените на 0.001. Наблюдайте изменения
графиков.
5) Сохраните файл под именем labkt2-2.
Регрессионный анализ зависимости R=f(t)
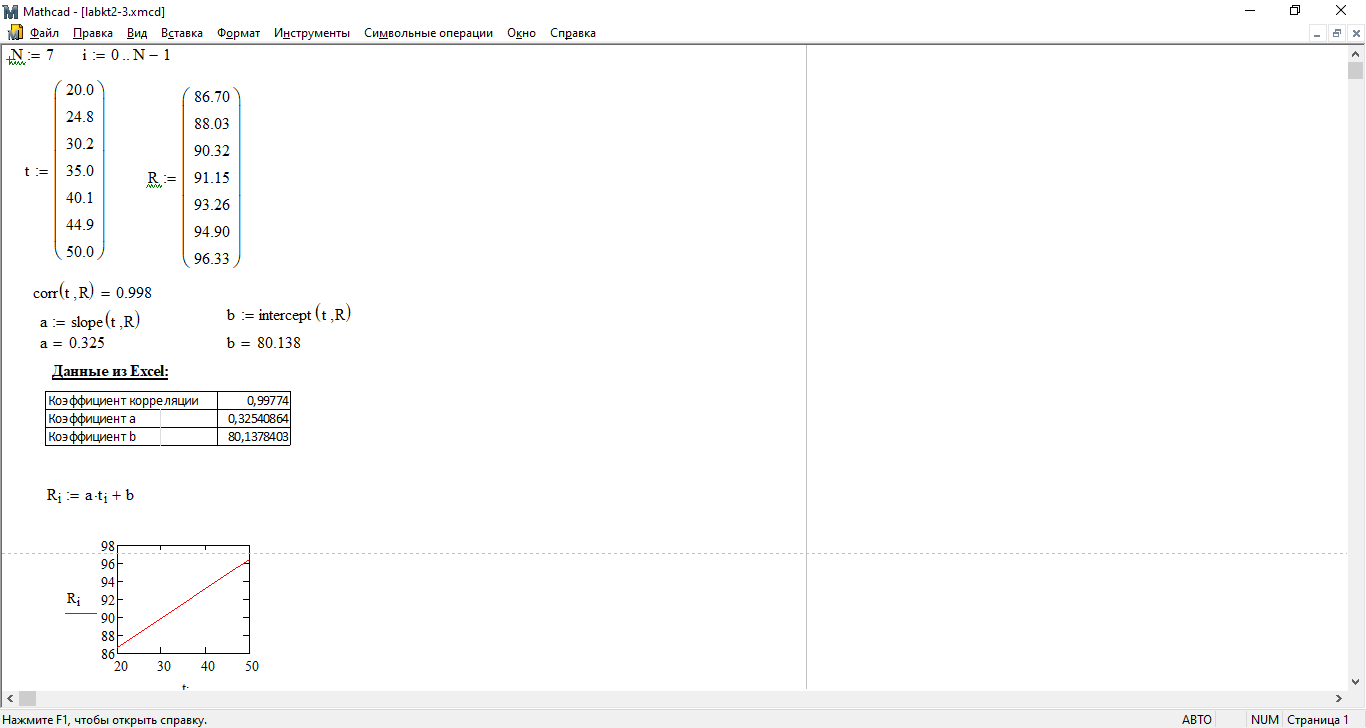
1) Задайте число измерений: N ∶= 7 i ∶=0..N-1.
2) Задайте векторы: t:= ; R:= (7 строк, 1 столбец) с числовыми данными из
пункта Iб-2.
3) Вычислите коэффициент корреляции: corr(t, R) = . . .
4) Определите коэффициенты линейной регрессии:
a ∶= slope(t, R) a = . . .
b ∶= intercept(t, R) b = . . .
Сравните с полученными при регрессионном анализе в Excel.
5) Задайте функцию: R(t) ∶= a ⋅ t + b и постройте график (X -Y зависимость)
регрессии R(t)i от ti.
6) Сохраните файл в рабочей директории под именем labkt2-3.
III. Построение в системе MathCAD графиков функций, заданных
явным выражением
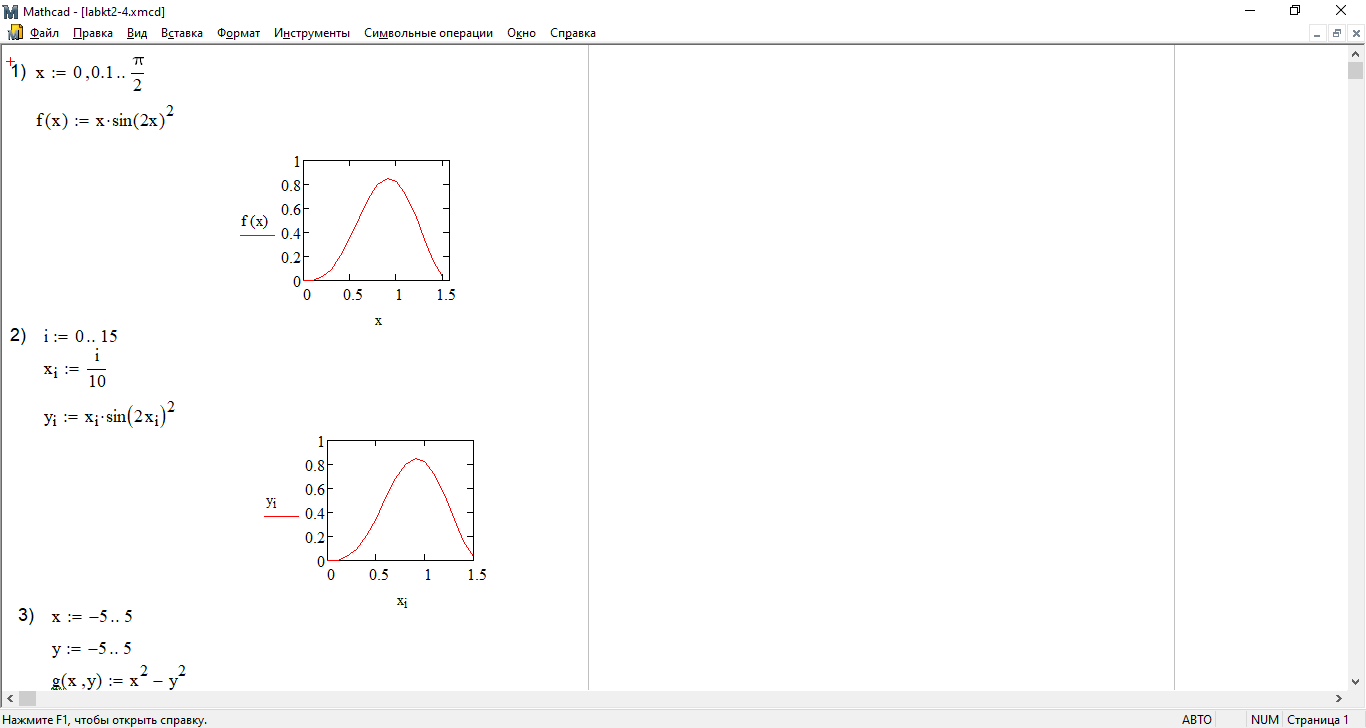
1) Задайте ранжированную переменную, меняющуюся от 0 до π/2 с шагом
0.1; определите функцию f (x) = x ⋅ sin(2x)2, постройте ее график.
2) Определите изменение целого индекса i от нуля до 15, xi = i/10, yi =
= xi sin(2xi)2, постройте график функции yi(xi).
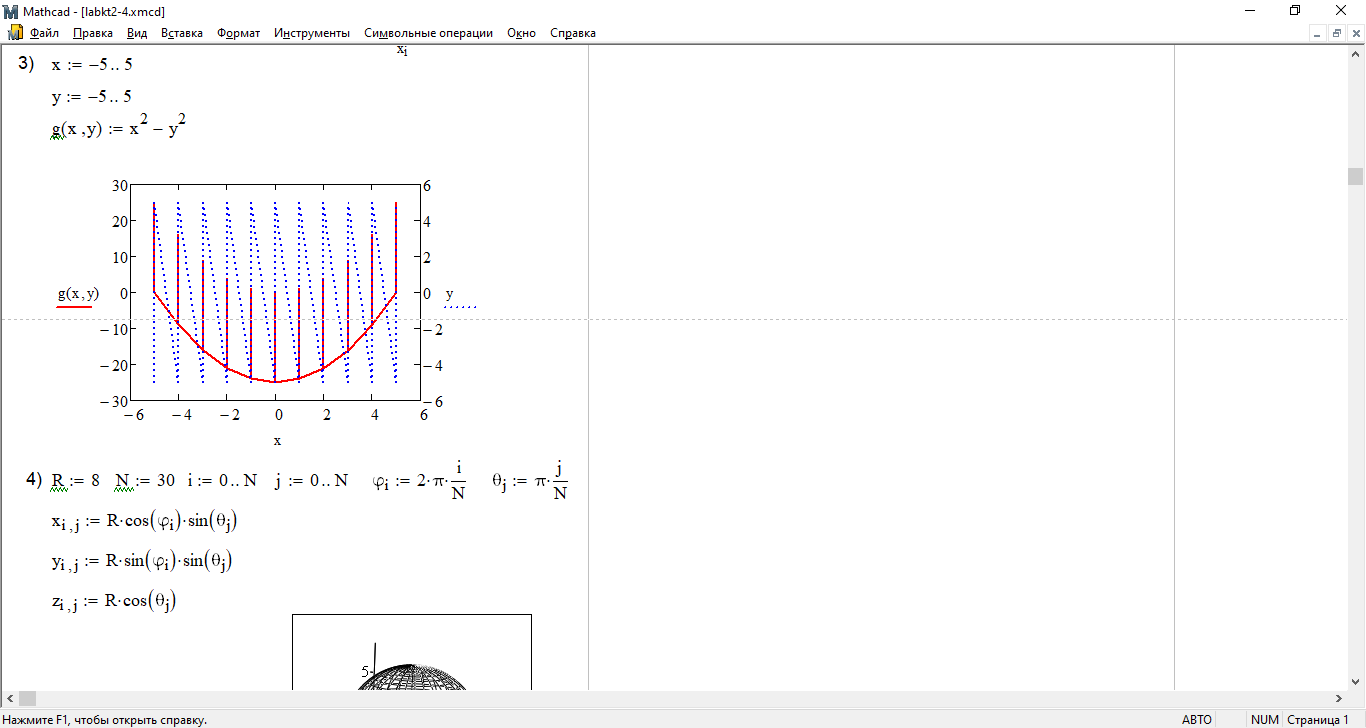
3) Постройте график функции g(x, y) = x2 − y2, где переменные x и y меняются от -5 до 5.
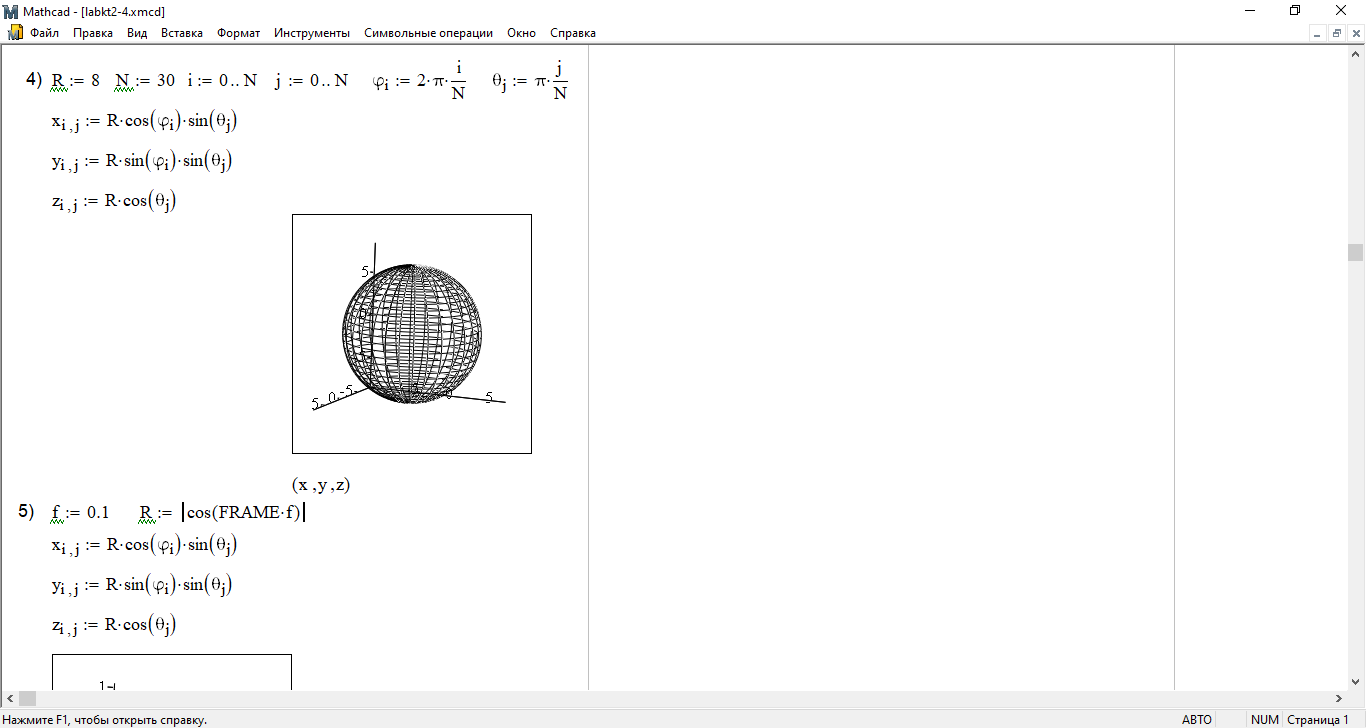
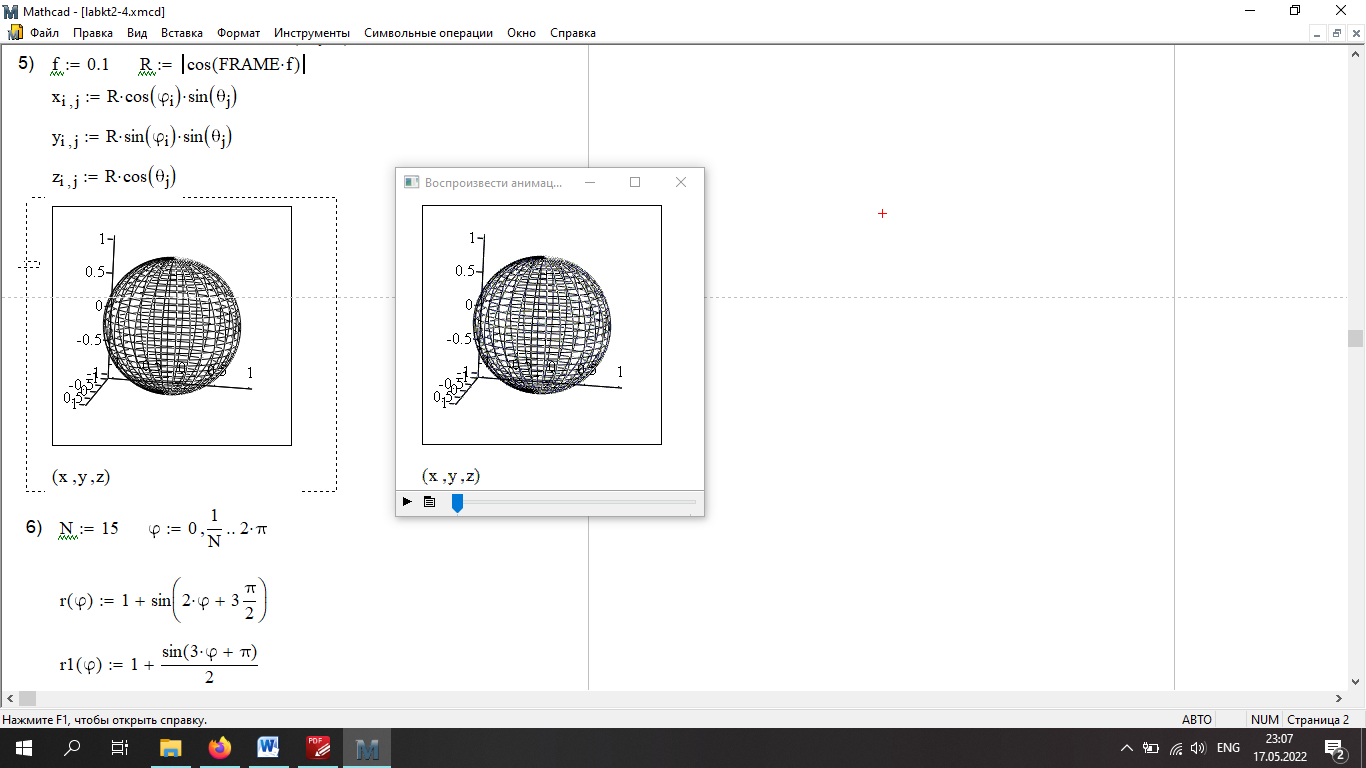
4) Изобразите сферу. Ее параметрическое представление имеет вид:
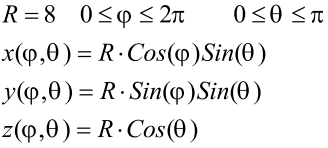
Число точек N = 30.
5) Добавьте дополнительное определение радиуса сферы R(f ) = ∣cos(FRAMEf )∣. Постройте анимационный график (число кадров равно 20, число кадров в секунду — 3. Просмотрите на Плеере получившуюся анимацию.
ВНИМАНИЕ!!! Перед построением анимации не забудьте отключить АВ-
ТОМАСШТАБ!
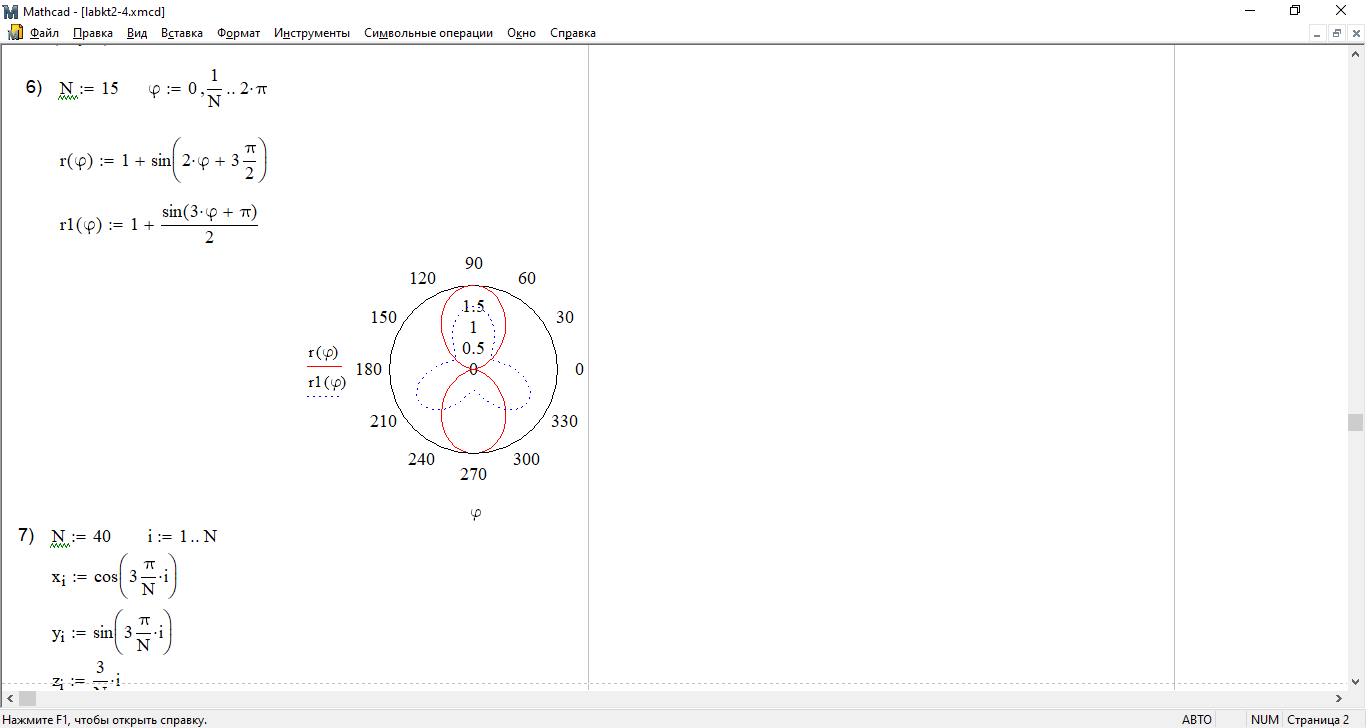
6) Постройте графики функций, заданных полярно:
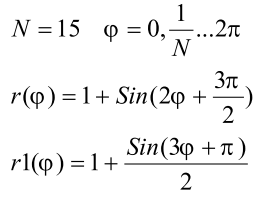
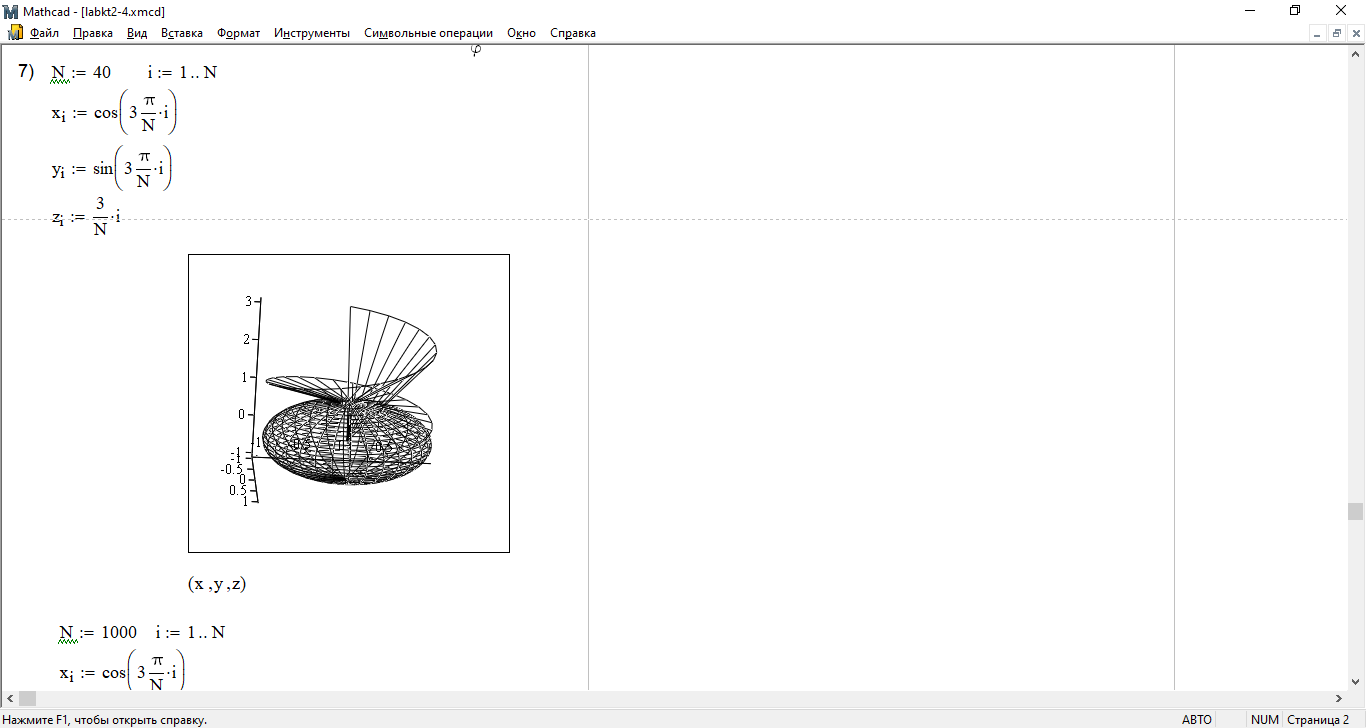
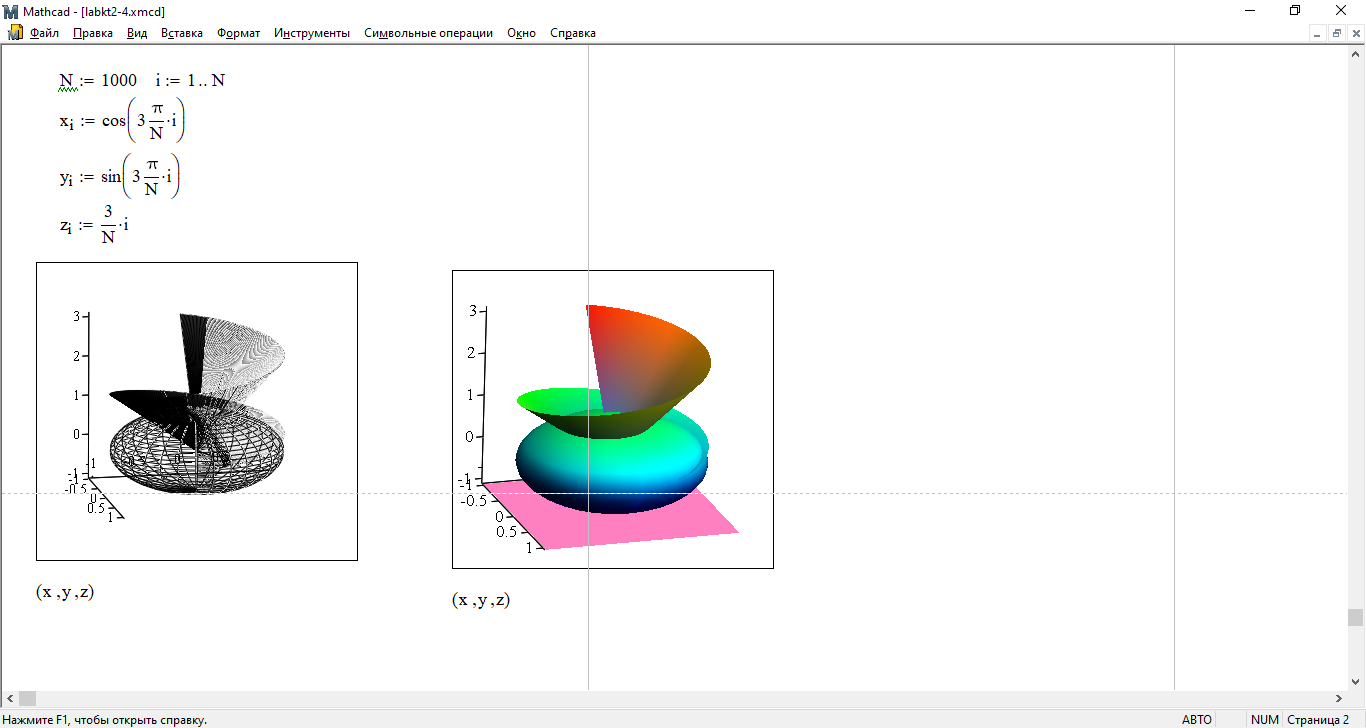
7) Изобразите пространственную кривую:
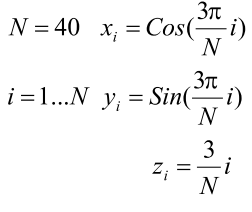
Увеличьте число точек N, повторите построение предыдущего графика
;
поэкспериментируйте, меняя различные параметры отображения графика.
8) Конечный результат сохраните в файле labkt2-4.
Результаты работы
Файл labkt2-1
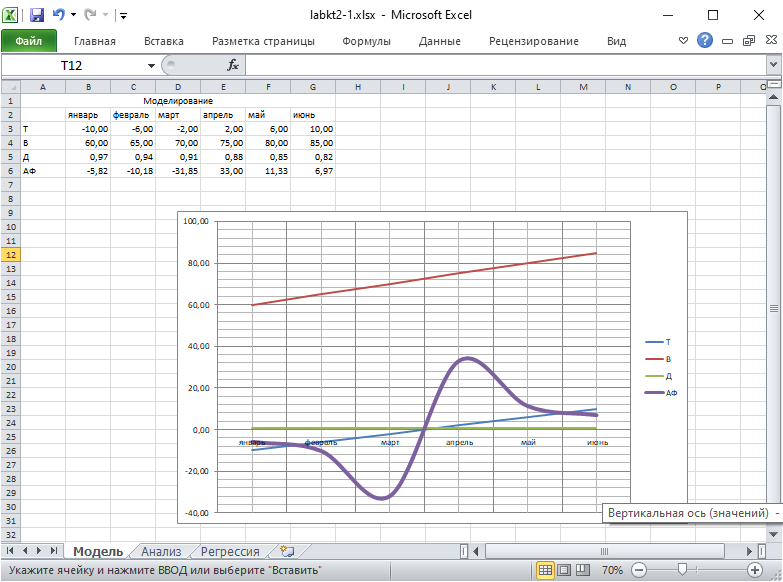
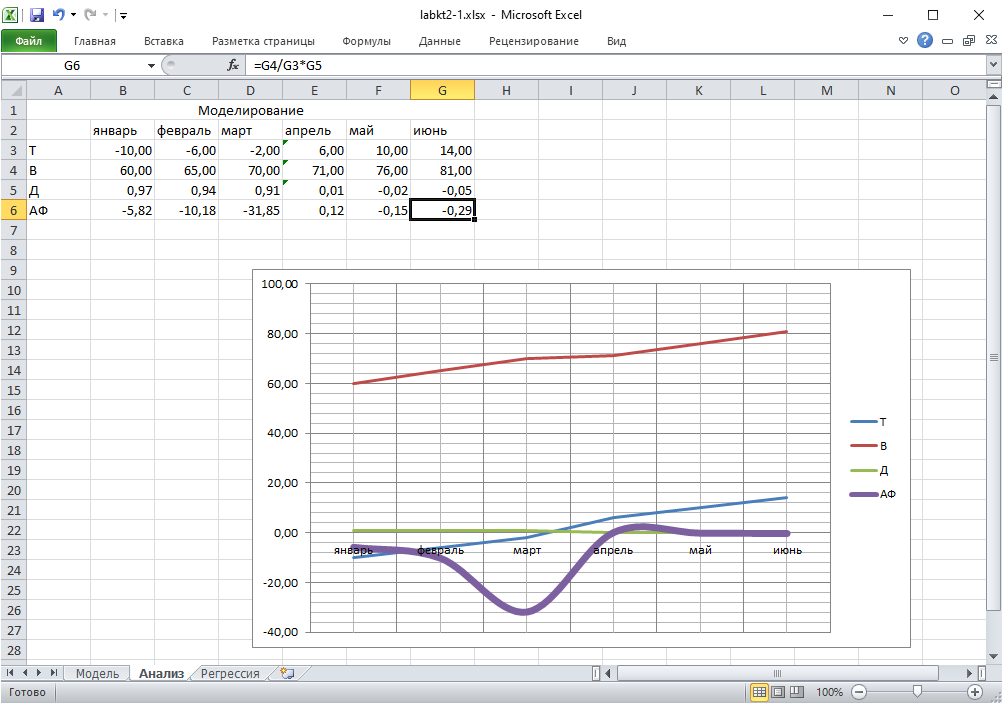
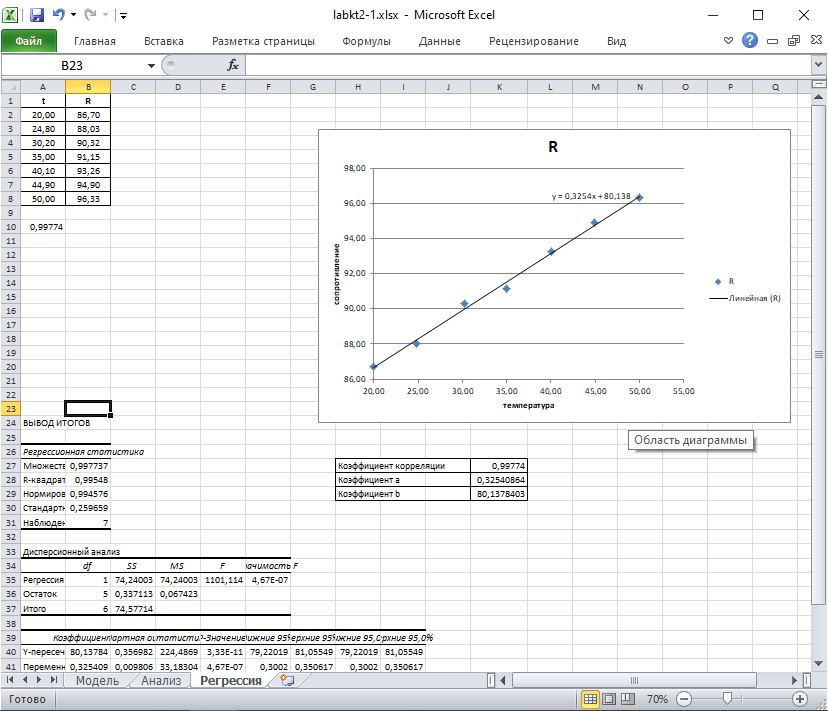
Файл labkt2-2
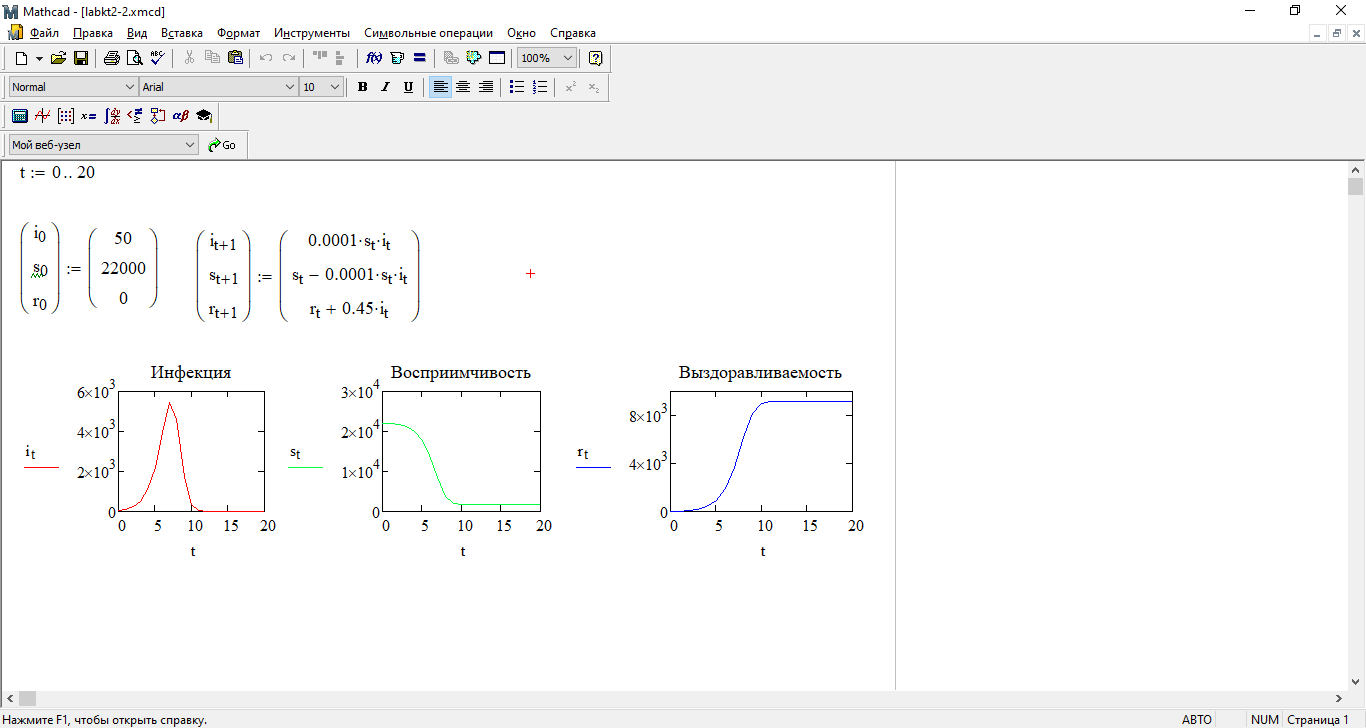
Файл labkt2-3
Файл labkt2-4
Список литературы
-
Изюмов А. А., Коцубинский В. П. Компьютерные технологии в науке и образовании : учебное пособие. — Томск: Эль Контент, 2012. — 149 с.