Файл: Лабораторная работа по курсу "Общая физика" определение удельного заряда электрона.doc

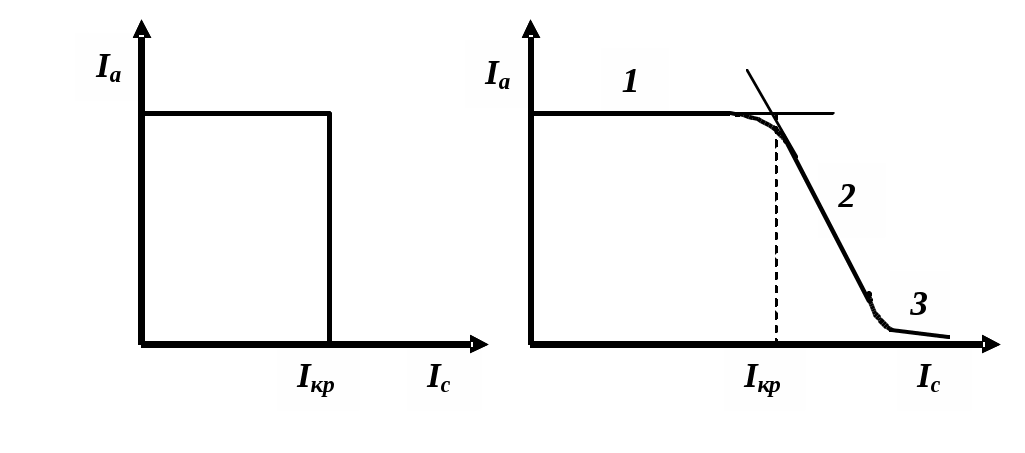
Рисунок 5.4 Зависимость анодного тока I_а от тока в обмотке соленоида I_{с .}


В работе для определения значения I_кр на полученном

графике I_а = f(I_с) проводят две прямые: одну (горизонтальную, область 1) через точки до спада анодного тока, другую – через точки, образующие линейный участок в области 2 спада анодного тока. Точка пересечения этих прямых (касательных к областям 1 и 2) будет наиболее точно соответствовать значению I_кр (рис. 5.4)

11. Ток эмиссии катода постоянен при постоянном токе накала. Почему при увеличении тока в соленоиде (I > I_кр) наблюдается снижение анодного тока?

На экспериментальной зависимости I_а = f(I_с) (рис. 5.4) можно выделить три прямолинейных участка. На первом участке все электроны, эмитированные катодом, достигают анода. На втором участке наблюдается плавное уменьшение анодного тока с ростом тока соленоида, так же начальные скорости электронов, вылетевших с поверхности катода, не равны нулю, а имеют различные значения (согласно распределению Максвелла). Третий участок обусловлен высокоэнергетичными электронами (их скорости много больше средней скорости). Доля их невелика (согласно распределению Максвелла). При данном значении индукции магнитного поля B радиус кривизны траектории электрона изменяется так, что более медленные электроны уже не попадают на анод, а быстрые электроны еще достигают анода. Поэтому с ростом тока соленоида анодный ток медленно спадает (рис. 5.4).

12. Почему в экспериментальной зависимости I_а= f(I_с) ненаблюдается резкого спада анодного тока при величине магнитной индукции B ≥ B_кр?

Это связано с тем, что в экспериментальной установке катод установлен не точно по оси анода. Кроме этого, радиус катода отличен от нуля, т.е. катод не представляет собой бесконечно тонкую нить. Он является цилиндром малого диаметра. Так же начальные скорости электронов, вылетевших с поверхности катода, не равны нулю, а имеют различные значения (согласно распределению Максвелла).
13. Два электрона с кинетическими энергиями Е₁ и Е₂движутся в магнитном поле, перпендикулярно направлению поля. Найти отношение их периодов обращения и радиусов траекторий.

Кинетическая энергия движущегося электрона равна:



(5.1)

где m, v – масса и скорость электрона.

Из выражения для 5.1 определим скорость электрона:

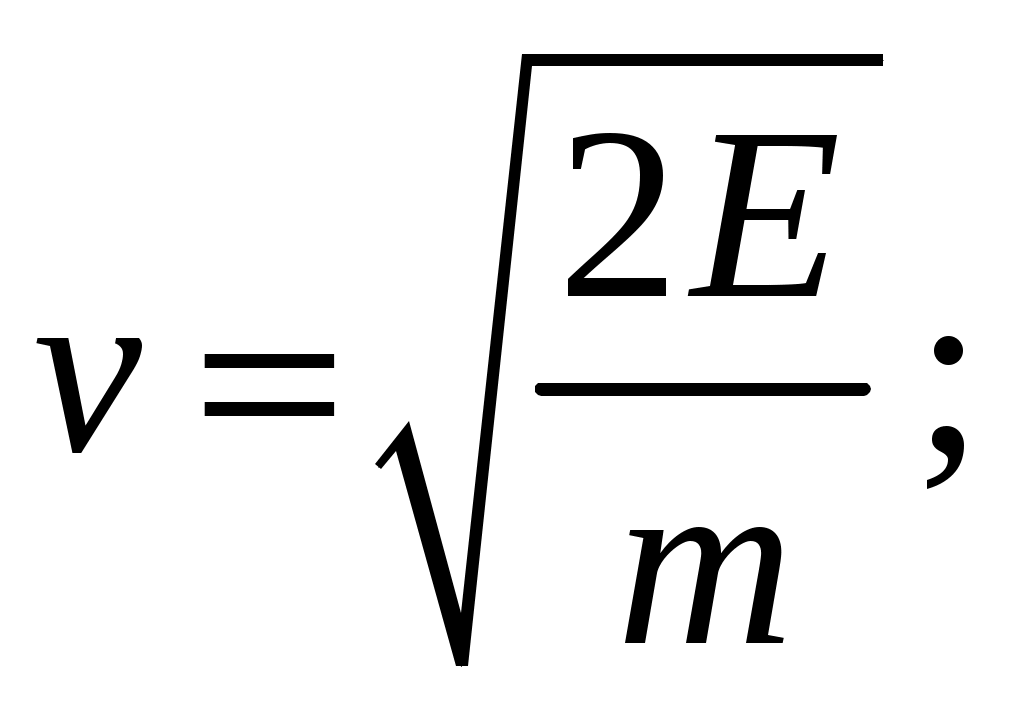(5.2)

Если электрон движется в однородном магнитном поле под действием силы Лоренца, а его скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то электрон будет двигаться по окружности радиуса: (5.3)

гдеe – заряд электрона.

И 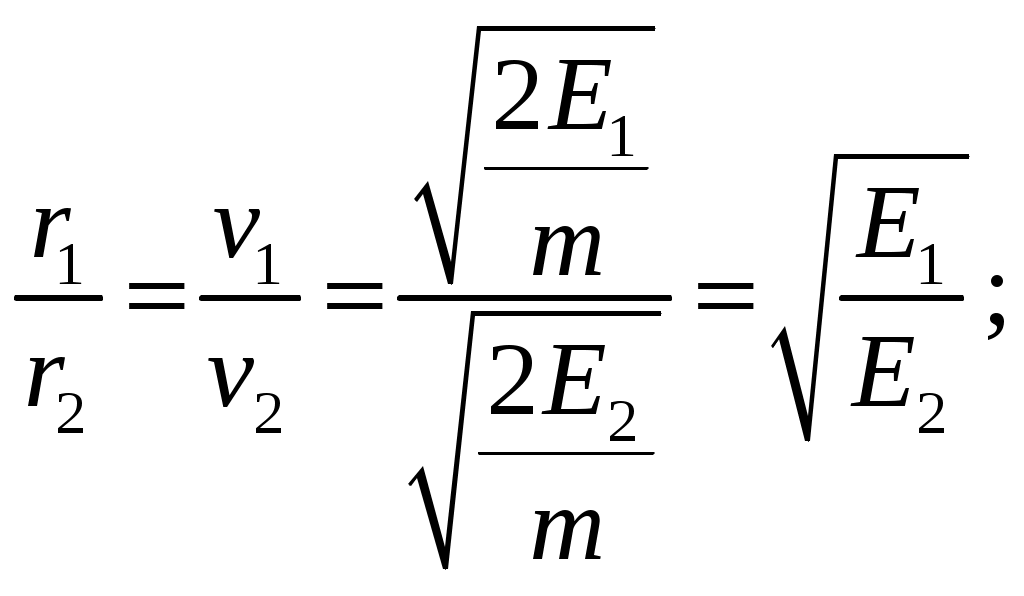з выражения 5.3 следует, что радиус кривизны траектории электрона пропорционален его скорости. На основании выражения 5.3 с учетом значения скорости электрона (5.2) найдем отношение радиусов траекторий движения электронов:
Период обращения частицы в однородном магнитном поле равен:


Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории r.

Следовательно, периоды обращения электронов будут равны: T₁ = T₂.
14. Определить частоту вращения (циклотронную частоту) частицы массы m и зарядом q в магнитном поле индукции B.

Е 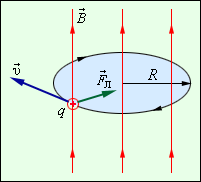сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса: (5.4)

где m,v,q – масса, скорость и заряд частицы.

 

Сила Лоренца в этом случае играет роль центростремительной силы (рис. 5.5).

Период обращения частицы в однородном

м агнитном поле равен:

Рисунок 5.5
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории r.

У гловая скорость движения заряженной частицы по круговой траектории:

(5.5)
П одставим в полученное выражение (5.5) выражение для радиуса траектории частицы (5.4), получим:

называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).
15. Выполняется ли принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях?

Движение частицы, находящейся в электромагнитном поле, описывается следующим уравнением.

Второй закон Ньютона: 

Заряженная частица, обладающая зарядом q, движется в электромагнитном поле согласно этому уравнению. Видим, что сила, действующая на частицу со стороны электромагнитного поля, определяется двумя векторными полями: поле  называется напряжённостью электрического поля, поле   - индукция магнитного поля. Они разделены, потому что влияние их на частицу различны. Поле  не содержит никаких характеристик частицы кроме заряда. Если v = 0, то второе слагаемое обращается в ноль. Это означает, что магнитное поле действует только на движущиеся частицы. Неподвижные заряды не чувствуют магнитного поля.

Следовательно, принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях, выполняется.
16. Электрон, обладающий скоростью v, попадает в однородное магнитное поле, индукция которого перпендикулярна скорости v. Окружность, какого радиуса описывает электрон?

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

где m, q – масса и заряд частицы.

Заряд электрона q = e, масса m = m_e.

Радиус описываемой электроном окружности:
17. Заряженная частица, пролетая некоторую область пространства, не отклоняется от первоначального направления движения. Можно ли на основании этого факта утверждать, что магнитное поле в этой области отсутствует?
Нельзя. Заряженная частица не отклоняется от первоначального направления движения в магнитном поле в следующих случаях:
1) В каждой точке магнитного поля существует такое направление, вдоль которого на движущуюся заряженную частицу магнитная сила не действует. Это направление можно назвать магнитной осью.
Существенно, что для каждой точки поля существует свое, отличное от других точек поля, направление магнитной оси. Это направление выбирают за направление вектора магнитной индукции .

При движении вдоль линий поля (угол между скоростью и вектором магнитной индукции  равен нулю) на частицу не действует сила - она движется прямолинейно.
2) На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно.

18. Пучок протонов, попадая в некоторую область пространства, отклоняется на некоторый угол. Можно ли на основании этого факта определить, каким полем вызвано отклонение, электрическим или магнитным?

Не имея данных ни о направлении поля действия поля, ни об изменении скорости частиц (или их кинетической энергии) при прохождении данной области установить природу поля нельзя.

19. Протон и электрон, имеющие одинаковую скорость, попадают в однородное магнитное поле, индукция В которого перпендикулярна скорости частиц. Как будут различаться их траектории?

Е сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

(5.19.1)
где q, m – заряд и масса частицы.

Заряды протона и электрона равны по величине, но противоположны по знаку: |q_p| = |q_e| = |e|

Исходя из формулы 5.19.1 радиус траектории частицы пропорционален ее массе и при равенстве скоростей, радиус траектории протона будет больше радиуса траектории электрона примерно в 1836 раз (соотношение масс протона и электрона m_p/m_e = 1836,15267).

Так как эти частицы имеют противоположные по знаку заряды, то и направление силы Лоренца, действующий на них в магнитном поле будет противоположно. Протон и электрон будут двигаться по окружностям в противоположных направлениях.

20. Протон и электрон, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории протона будет больше радиуса кривизны траектории электрона?

Частица, пройдя ускоряющую разность потенциалов U, приобретает кинетическую энергию, равную:

( 5.20.1)

где q, m – заряд и масса частицы;

v – скорость, которую приобретает частица.
Е сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

(5.20.2)



Из уравнения (5.20.1) найдем скорость частицы:

Полученное выражение для скорости частицыv подставим в уравнение (5.20.2):

(5.20.3)

Заряды протона и электрона равны по величине и противоположны по знаку: |q_p| = |q_e| = |e|

С учетом равенства абсолютной величины зарядов и на основании формулы (5.20.3) запишем соотношение радиусов кривизны траекторий частиц:



В справочной литературе приведено соотношение масс протона и электрона − m_p/m_e = 1836,15267.

О кончательно получаем:

21. Протон и электрон влетают в однородное магнитное поле с одинаковой скоростью. Во сколько раз радиус кривизны траектории протона будет больше радиуса кривизны траектории электрона?
Е сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции то частица будет двигаться по окружности радиуса:

(5.21.1)
где q, m – заряд и масса частицы;

Заряды протона и электрона равны по величине и противоположны по знаку: |q_p| = |q_e| = |e|

На основании формулы (5.21.1)запишем соотношение радиусов кривизны траекторий частиц при условии равенства их скоростей:


В справочной литературе приведено соотношение масс протона и электрона − m_p/m_e = 1836,15267.

О кончательно получаем:
22. Показать, что какой бы скоростью v ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каким бы ни был угол между векторами v и В, время Т, за которое он опишет виток винтовой линии, будет одним и тем же.



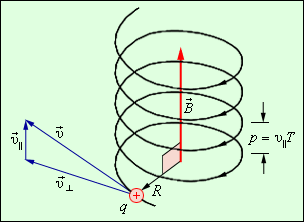
Рисунок 4.18.5.

Движение заряженной частицы по спирали в однородном магнитном поле.

Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей вектора , а шаг спирали p – от модуля продольной составляющей (рис. 4.18.5). Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции.

В направлении перпендикулярном полю частица движется по инерции равномерно, со скоростью
В направлении поля частица движется по инерции равномерно, со скоростью
Угол α в этих выражениях равен углу между скоростью и вектором магнитной индукции  .

В направлении, перпендикулярном вектору магнитной индукции , частица будет двигаться по окружности радиуса:
где m,v,q – масса, скорость и заряд частицы.

 

Период обращения частицы в однородном магнитном поле равен:




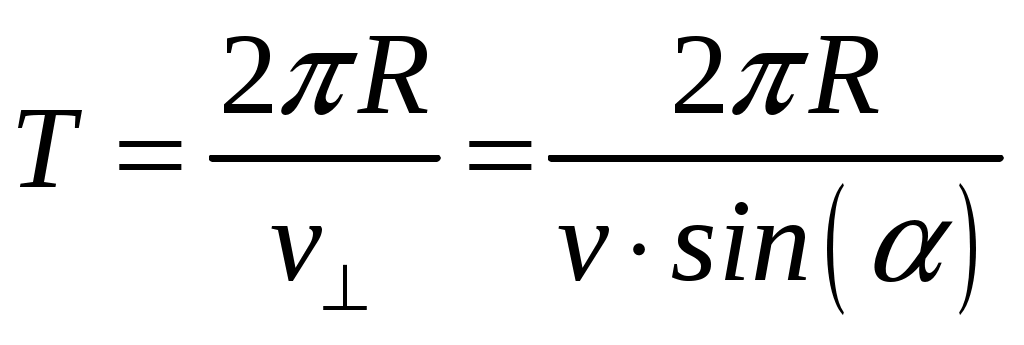
Подставляя сюда вместо R его выражение, имеем:



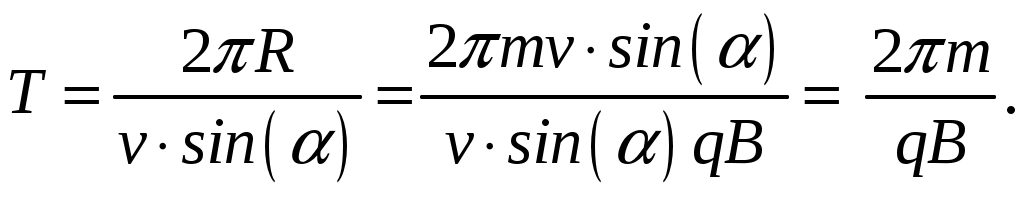
Следовательно, какой бы скоростью v ни обладал электрон, влетающий в однородное магнитное поле с индукцией В, и каким бы ни был угол между векторами v и В, время Т, за которое он опишет виток винтовой линии, будет одним и тем же.
23. Показать, что радиус кривизны траектории заряженной частицы, движущейся в однородном магнитном поле, перпендикулярном её скорости, пропорционален импульсу частицы.

Сила Лоренца является центростремительной силой и при движении частицы в данных условиях справедливо равенство:


где q, m – заряд и масса частицы;

v – скорость электрона;

B – индукция магнитного поля;

r – радиус кривизны траектории.
П од действием магнитного поля траектория движения электрона станет криволинейной. Из приведенного равенства следует, что радиус кривизны траектории зависит от скорости электрона и от величины магнитной индукции поля соленоида:
Импульс частицы равен: p = mv, подставляя в вышестоящее равенство, получим: