Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования

Санкт-Петербургский государственный горный университет

Е.И. Крапивский, О.В. Кабанов И.А. Вишняков, В.И. Климко

Численное моделирование неизотермического

течения нефти в трубопроводе в программном комплексе ANSYS/FLUENT

Учебное пособие для студентов высших учебных заведений, обучающихся по направлениям подготовки дипломированных

специалистов «Нефтегазовое дело» и «Технологические машины и оборудование»

Санкт-Петербург 2012

УДК 621.643.053

ББК

К

Численное моделирование неизотермического течения нефти в трубопроводе в программном комплексе ANSYS/FLUENT: Учебное пособие/ Е.И. Крапивский, О.В. Кабанов И.А. Вишняков, В.И. Климко. – СПб.: СПГГУ, 2012. – 128 с., ил.
Приведены основные сведения по методике составления математического описания процессов неизотермического течения нефти в трубопроводе с использованием уравнений Рейнольдса, Навье-Стокса, Пуазейля. Рассмотрены случаи ламинарного и турбулентного течения. Приведены сведения о моделях турбулентности, используемых в алгоритмах численного моделирования в программном комплексе ANSYS/FLUENT. Подробно рассмотрен порядок использования комплекса на примере моделирования «горячего» нефтепровода, а также смешивающего колена.

Пособие предназначено для студентов, обучающихся по программам бакалаврской и магистерской подготовки, а также может быть использовано аспирантами при исследовании процессов трубопроводного транспорта нефти и инженерно-техническими работниками при проектировании и эксплуатации трубопроводного транспорта нефти и систем гидро- и пневмопривода горных и металлургических машин.


Научный редактор проф. Е.И.Крапивский


Рецензенты: зав. кафедрой физики Ухтинского государственного технического университета

---

, д.ф.-м. профессор В.О. Некучаев;

кафедра Подъемно-транспортных, путевых и строительных машин Петербургского государственного университета путей сообщения.

Оглавление

Введение………………………………………………………………..4

Глава 1. Общие сведения…………………………………………….5

Глава 2. Основы математического моделирования процесса
неизотермического течения жидкости в трубопроводе………….6

2.1 Уравнения Навье-Стокса…………………………………………..6

2.2 Ламинарное движение в трубах………………………………….13

2.3 Турбулентное течение жидкости………………………………...18

2.3.1 Общие сведения…………………………………………………18

2.3.2 Уравнения Рейнольдса………………………………………….21

2.3.3 Полуэмпирические теории турбулентности…………………..22

2.3.4 Турбулентное течение в трубах………………………………..24

2.3.5 Степенные законы распределения скорости………………….32

2.3.6 Потери давления (напора) при турбулентном течении в
трубах………………………………………………………………….32

2.4 Теплообменные процессы при движении жидкости в трубе. Уравнение теплового баланса Фурье………………………………..34

Глава 3. Программный пакет ANSYS/FLUENT…………………39

3.1 Общие сведения…………………………………………………...39

3.2 Расчетные сетки…………………………………………………...42

3.3 Об основных моделях турбулентности, представленных в ANSYS/FLUENT………………………..…...………………………...45

Глава 4. Пример расчета «горячего» подземного
трубопровода в среде ANSYS/FLUENT………………….…...……48

4.1 Постановка задачи……………………………………….………...48

4.2 Порядок расчета…………………………………….……………..48

4.3 Визуализация полученных результатов, их анализ………….….90

4.4 Задание для самостоятельной работы…………………..….…….97

Глава 5. Пример расчета смешанного потока (горячего с
холодным)………………………………………..……………………98

5.1 Постановка задачи…………………………………..……………..98

5.2 Порядок расчета……………………………………….…………..99

5.3 Визуализация результатов расчета…………………….………..121

5.4 Оптимизация конструкции смешивающего колена……….…...123

Библиографический список……………………………….………127

Введение

При изучении теоретических вопросов гидродинамики, термодинамики, численного моделирования гидравлических и теплообменных процессов рекомендуется пользоваться литературой [1-23].

---

Данное учебное пособие рекомендуется студентам, аспирантам, инженерам и другим заинтересованным читателям с целью ознакомления с основами вычислительной гидродинамики применительно к трубопроводному транспорту нефти на основе использования программного комплекса ANSYS/FLUENT 12.1.

Вычислительная гидродинамика – это раздел науки, решающий проблему моделирования тепломассопереноса в различных технических и природных объектах. Основной задачей ВГД является численное решение уравнений Навье-Стокса, описывающих динамику жидкости. Дополнительно учитываются различные физико-химические эффекты: горение, турбулентность или потоки сквозь пористую среду. Эти уравнения составляют математическую модель тепломассопереноса. Вычислительная гидродинамика как прикладная наука сформировалась в середине 20 века. С развитием высокопроизводительных компьютеров, которые стали доступны по цене большому числу пользователей, в 70-х годах началось бурное развитие коммерческих программ вычислительной гидродинамики. В конце 90-х появились программы в области вычислительной гидродинамики, предназначенные для персональных компьютеров.

Авторы благодарят за помощь и поддержку инженера по гидрогазодинамике КАДФЕМ Си-Ай-Эс (филиал в СЗФО) Т.А. Тимофееву, зав. кафедрой ПТПСМ ПГУПС В.А. Попова, доцента кафедры ПТПСМ ПГУПС С.К. Коровина, зав. кафедрой физики УГТУ, д.ф.-м.н. профессора В.О. Некучаева за ценные идеи и помощь в разъяснении сложных вопросов простым языком.

Глава 1. Общие сведения

На современном этапе научных исследований вычислительный эксперимент является одним из важных направлений при изучении задач аэродинамики, тепломассообмена и горения. Информация, полученная с помощью численных расчетов, позволяет не только правильно осмыслить и понять физические эффекты, наблюдаемые, например, на экспериментальных установках, но и в некоторых случаях заменить физический или натуральный эксперимент компьютерным как более дешевым. Иногда компьютерный эксперимент является единственно возможным. Учитывая дальнейший прогресс в области развития вычислительной техники, можно ожидать, что в ближайшем будущем возрастет роль компьютерного моделирования как в создании новых образцов промышленности, так и в исследовании процессов и явлений, происходящих в окружающем нас мире.

---

Разработкой методов расчета и особенно созданием программ и пакетов прикладных программ для решения научно-технических задач занято большое число исследователей. Ввиду разнообразия задач при создании программ даже по одному алгоритму или численному методу неизбежен параллелизм в работе, когда различные исследователи при создании программ вынуждены проделывать всю работу от начала до конца. Простой анализ показывает, что у различных созданных программ имеются общие части, которые целесообразно однократно запрограммировать и в дальнейшем многократно использовать. С другой стороны, расширение класса задач требует создания большого числа программ одноразового (несерийного) использования. Это обусловливает неоправданные затраты ресурсов (умственных, компьютерных) на создание и отладку программ. Кроме того, замедляется и сам процесс исследований. Данные обстоятельства приводят к необходимости перехода на другой путь создания программ, а именно на создание пакетов программ, ориентированных на решение целых классов задач. Сейчас созданы и успешно развиваются пакеты программ для решения отдельных классов задач математической физики (вычислительная гидродинамика, тепломассообмен, прочностной расчет, электродинамика и др.).

Глава 2. Основы математического моделирования процесса неизотермического течения жидкости в трубопроводе

2.1 Уравнения Навье-Стокса

Стационарные или нестационарные течения вязкого сжимаемого газа описываются уравнениями Навье-Стокса, а течения идеальной среды – уравнениями Эйлера которые для безвихревых течений сводятся к уравнениям потенциала.

В зависимости от размерности решаемой задачи используется трехмерная формулировка исконных уравнений или их сокращенный вариант – свойство независимости от одной или нескольких пространственных координат (плоские или осесимметричные течения). Моделирование течений с преимущественным направлением развития потока (течения в пограничных слоях или струях) проводится на основе параболизованных уравнений Навье-Стокса.

Для расчетов турбулентных течений используется осреднение или фильтрация уравнений Навье-Стокса с последующим замыканием полученных уравнений.

---

Уравнения Навье-Стокса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье-Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса.

В векторной форме система состоит из уравнений движения и неразрывности.

Для вывода уравнений Навье-Стокса [15] выделим в сплошной среде объем в форме параллелепипеда ABCDA₁B₁C₁D₁ (рисунок 1.1) с ребрами, параллельными осям координат и размерами соответственно dx, dy, dz.



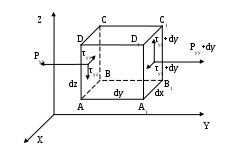
Рисунок 1.1 – Напряжения в элементарном объеме сплошной среды

Чтобы не усложнять рисунок, на нем показаны компоненты напряжений, приложенных только к граням, которые нормальны оси y, т.е к ABCD и A₁,B₁C₁D₁. При непрерывном изменении параметров среды в пространстве в функции от x, y, z, разность их значений на элементарном расстоянии определим ограничившись первым членом ряда Тейлора, зависящим от частных производных функции по координатам. На расстоянии dy разность напряжений, приложенных к нормальным оси y граням ABCD и A₁B₁C₁D₁ равна и умножив эти величины на площадь грани ABCD, т.е. dxdz, получим соответствующие, действующие на параллелепипед усилия. Аналогичным образом могут быть получены разности компонентов напряжений, приложенных к граням, нормальным осям x (AA₁D₁D и BB1C₁C) и z (CC₁D₁D и AA₁B₁B). Они будут равны соответственно и а после умножения на площади граней, соответственно dydz и dxdy, дадут остальные

---

Смотрите также файлы

• Темы занятий.docx

• Химический факультет отчет по учебной практике.docx

• Разговор о важном 23 января 2023 г.docx

• Тема вкр Моделирование специальной физической подготовки в тренировочном процессе биатлонистов оглавление.docx

• Бортовые магнитофоны.pptx