Файл: Учебное пособие для студентов высших учеб ных заведений, обучающихся по направлениям подготовки дипломированных специалистов Нефтегазовое дело.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 373
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, приложенные к рассматриваемому объему, поверхностные силы.
Обозначим проекции ускорений массовых сил параллелепипеда на оси координат через X, Y и Z, а проекции ускорения движения его центра через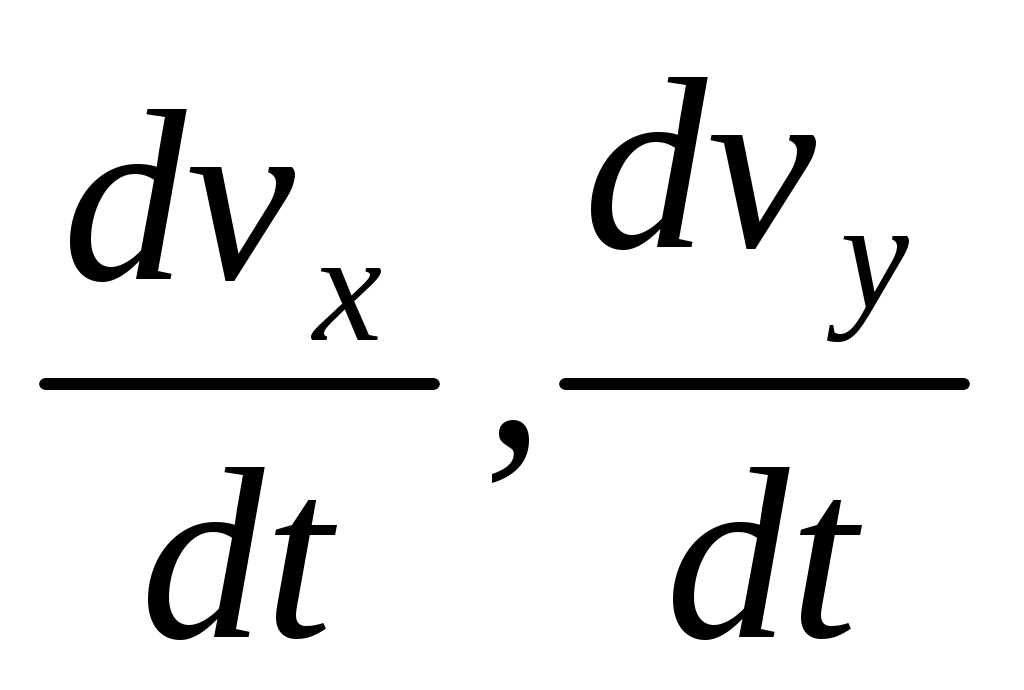 и
и 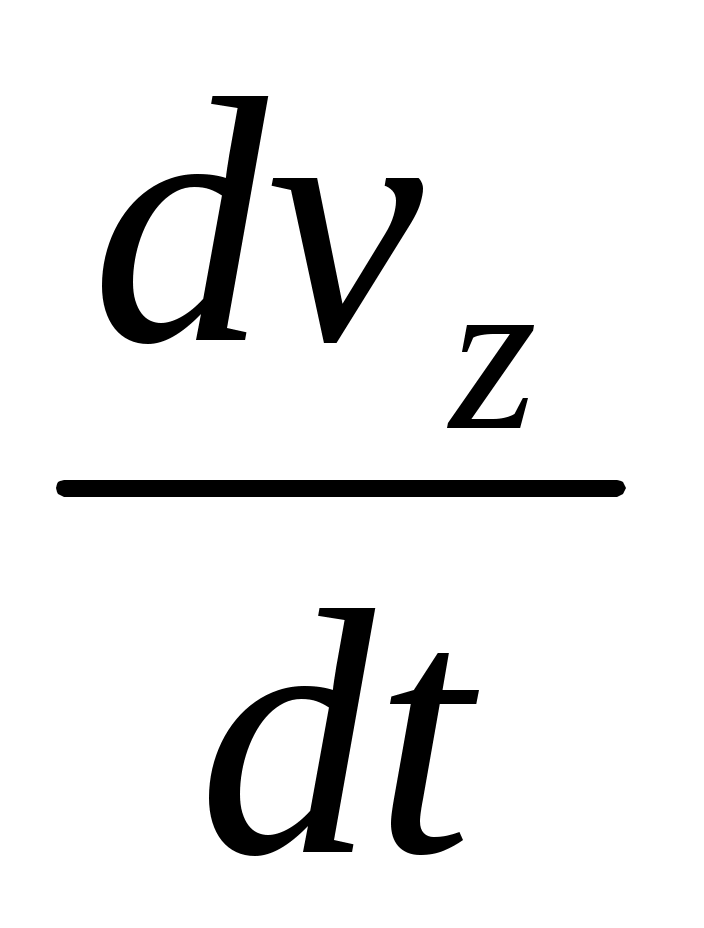 . После умножения этих ускорений на массу параллелепипеда
. После умножения этих ускорений на массу параллелепипеда 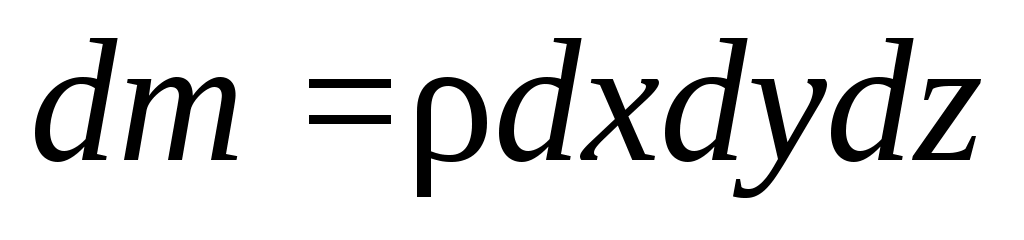 , составив соотношения для суммы приложенных к объему сил и сократив их предварительно на dxdydz, напишем уравнения его движения в проекциях на координатные оси в виде
, составив соотношения для суммы приложенных к объему сил и сократив их предварительно на dxdydz, напишем уравнения его движения в проекциях на координатные оси в виде
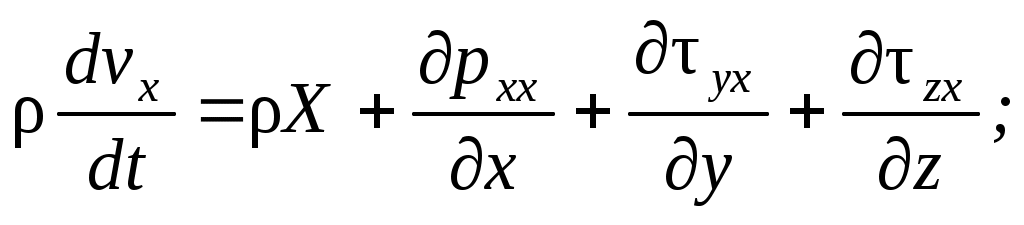
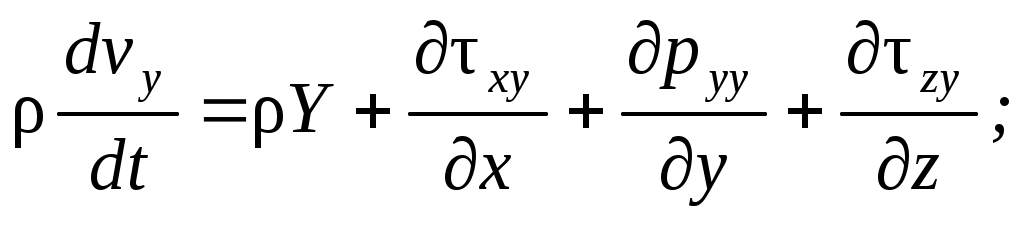 (2.1)
(2.1)
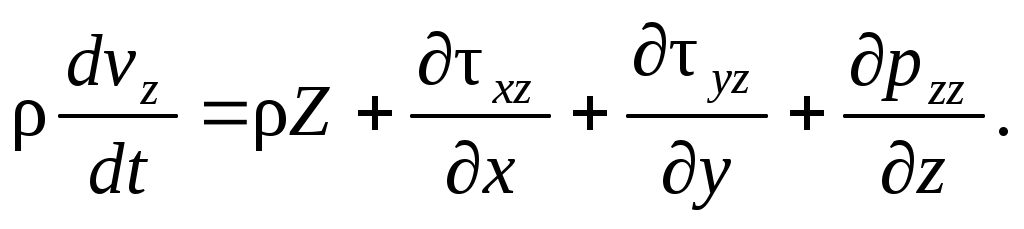
Эти соотношения называются уравнениями динамики сплошной среды в напряжениях.
Первое из полученных уравнений (2.1) можно привести к виду [15]:
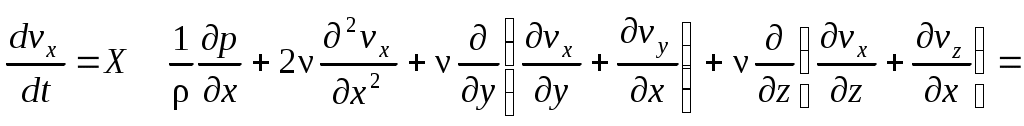
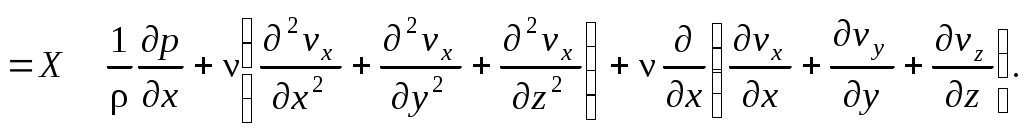
Оставшиеся два уравнения преобразуются аналогично.
Для несжимаемой жидкости выражение в скобках в последнем члене этого соотношения равно нулю.
Воспользуемся значком для обозначения дифференциального оператора вида
для обозначения дифференциального оператора вида
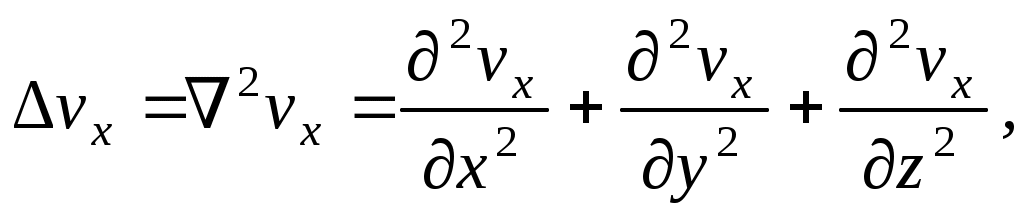 (2.2)
(2.2)
который называется оператором Лапласа.
Кроме того, после представления полной производной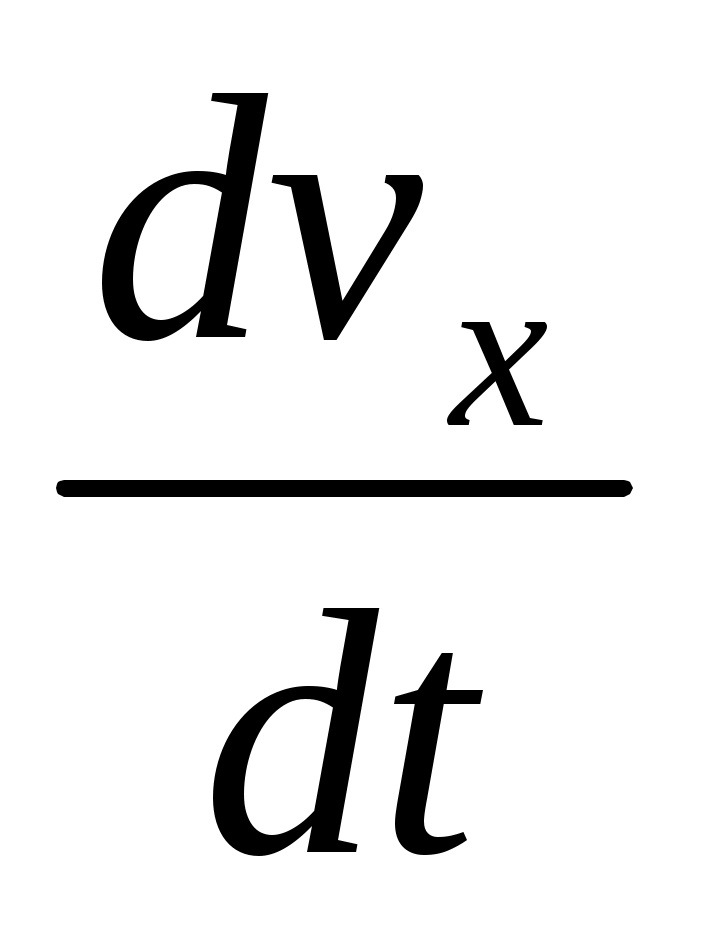 через частные, а также с учетом того, что
через частные, а также с учетом того, что 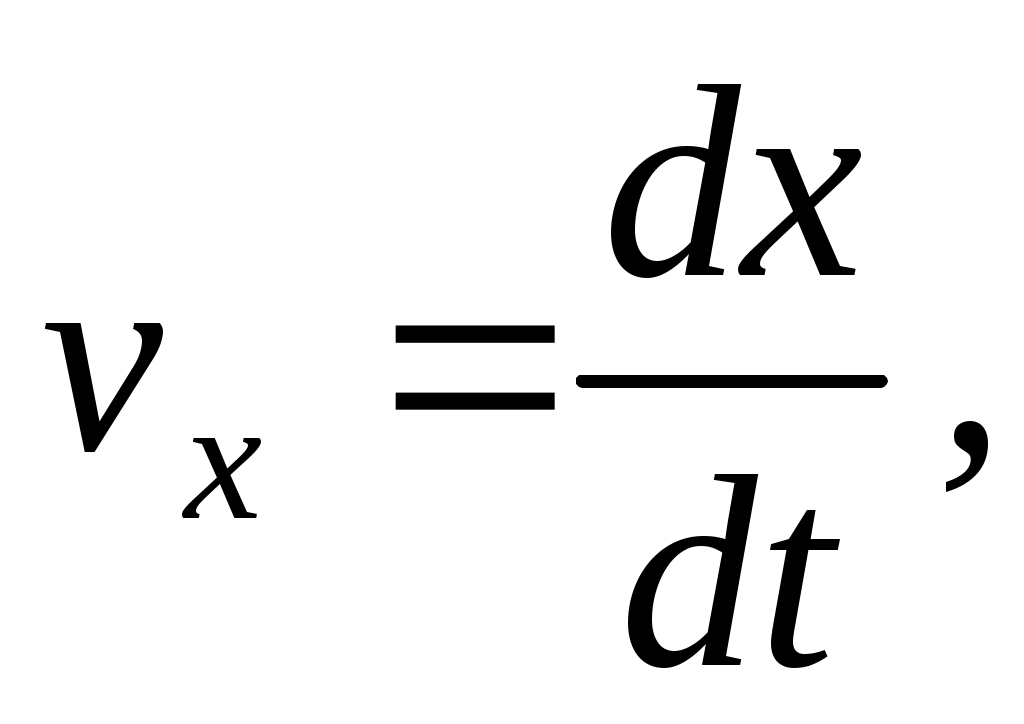
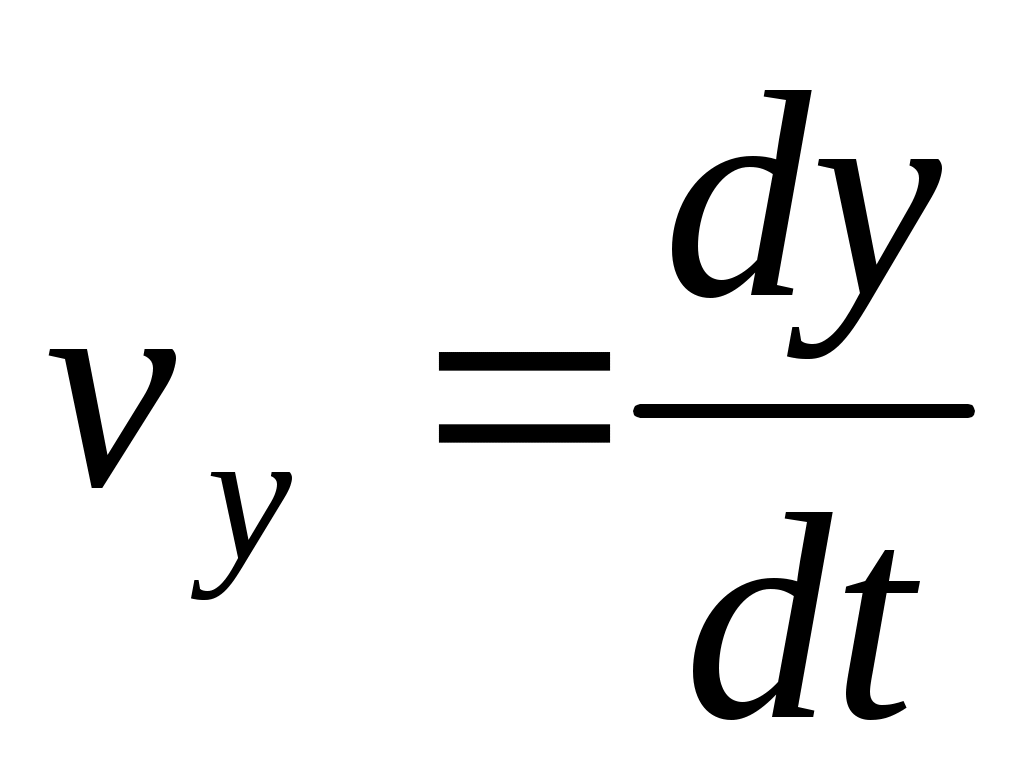 и
и 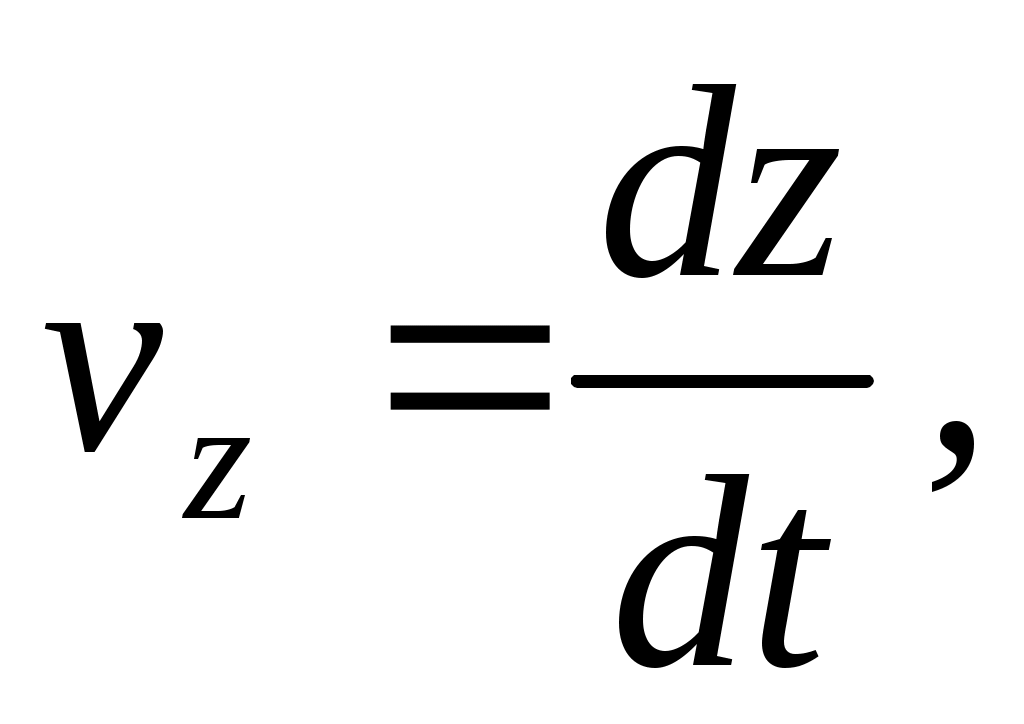 можно написать
можно написать
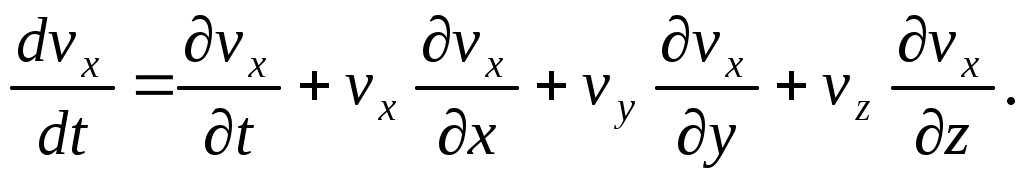 (2.3)
(2.3)
В итоге, первое из равенств, а по аналогии с ним, и вся система (2.1) для несжимаемой жидкости примет вид
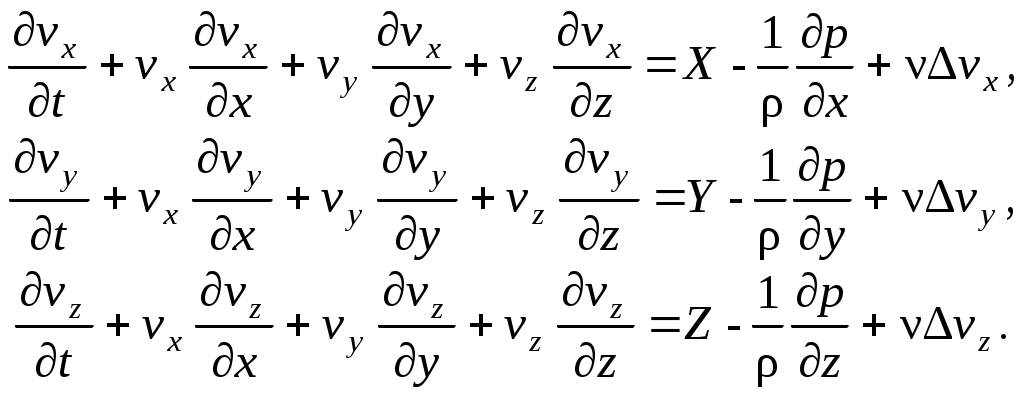
(2.4)
Равенства (2.4) называются уравнениями Навье – Стокса для жидкости. Для идеальной жидкости и газа (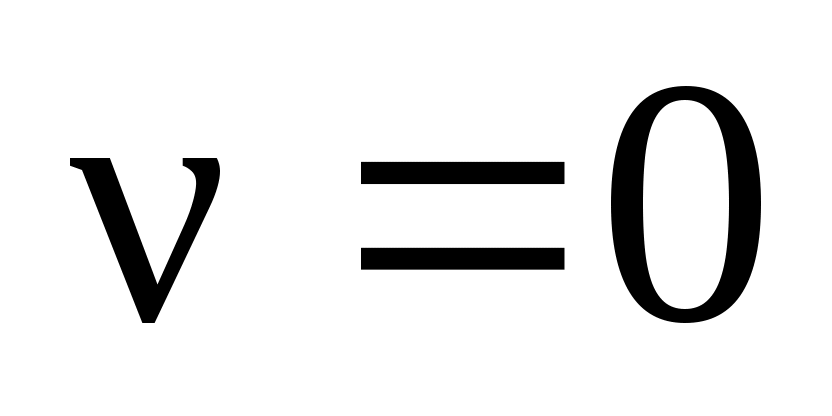 ) уравнения (2.4) принимают вид
) уравнения (2.4) принимают вид
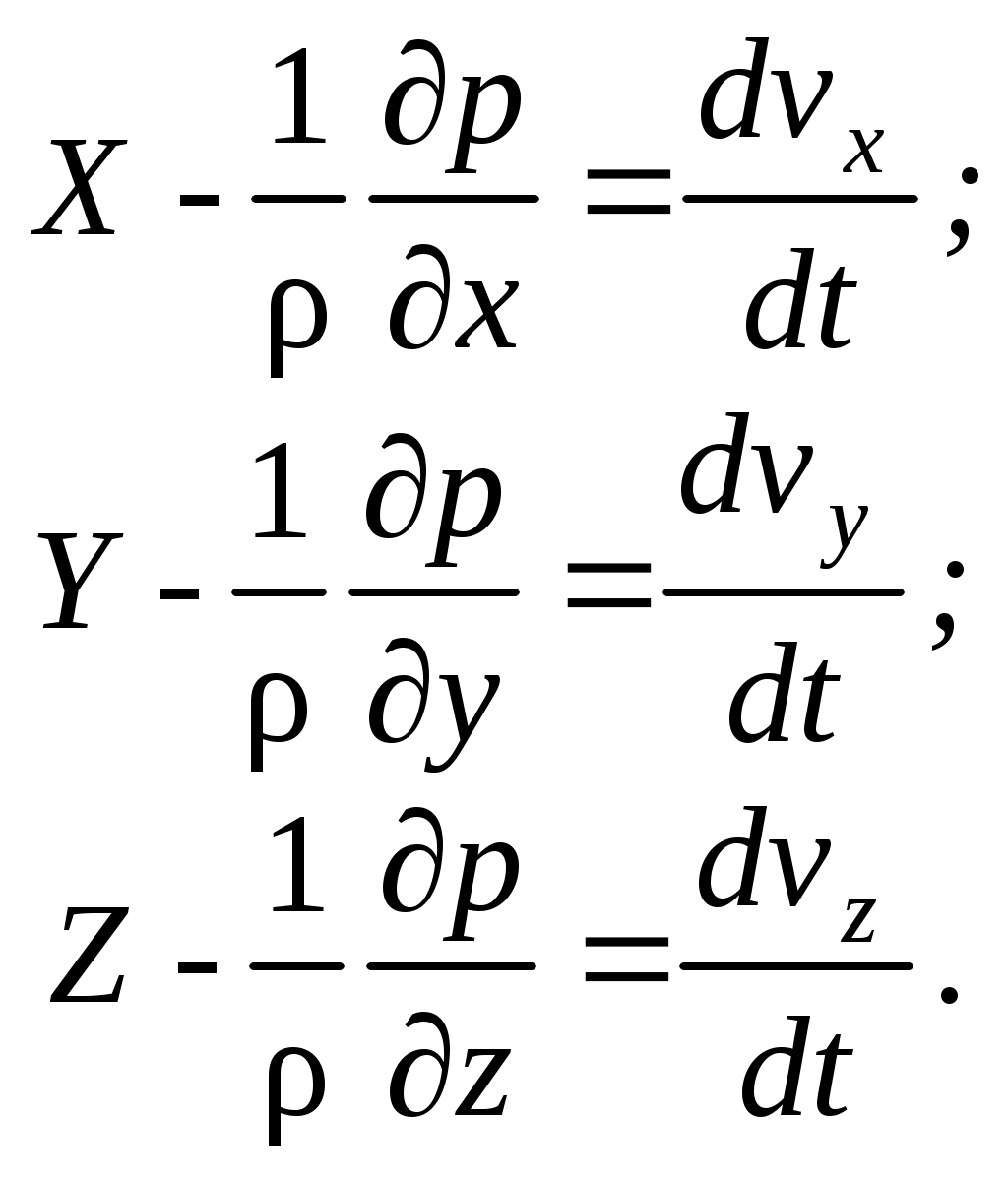 (2.5)
(2.5)
Уравнения (2.5) называются гидродинамическими уравнениями Эйлера.
Система уравнений (2.5) может быть представлена в векторной форме
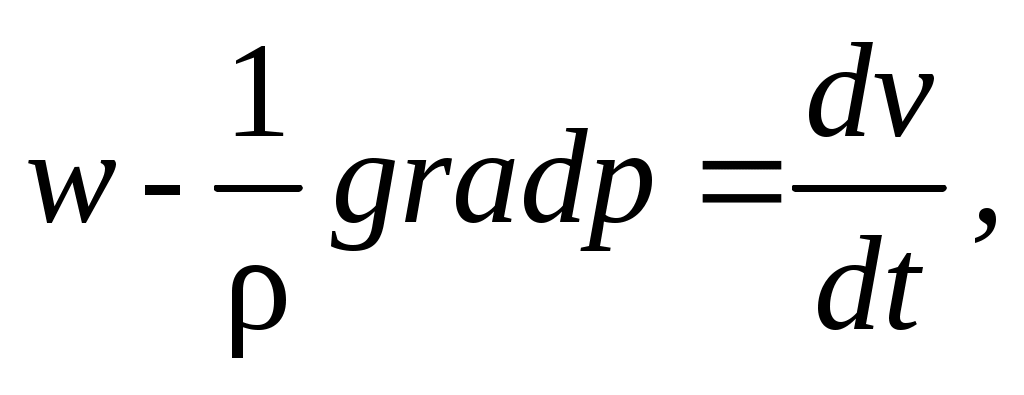 (2.6)
(2.6)
здесь w – ускорение массовых сил; p рассматривается как скалярная функция координат x, y, z, а gradp , как векторная функция x, y, z.
Кроме того выражение
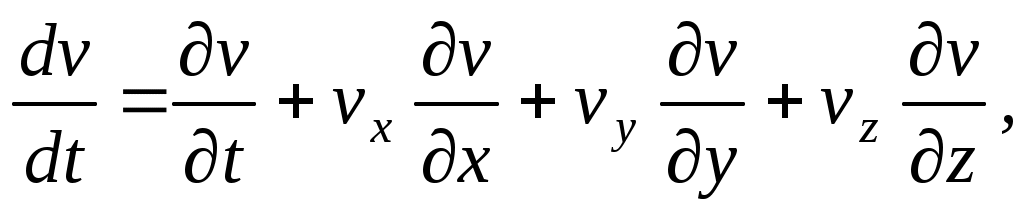 (2.7)
(2.7)
представляющее собой полную производную скорости от времени в гидромеханике называется также индивидуальной или субстанциональной производной. Ее составляющая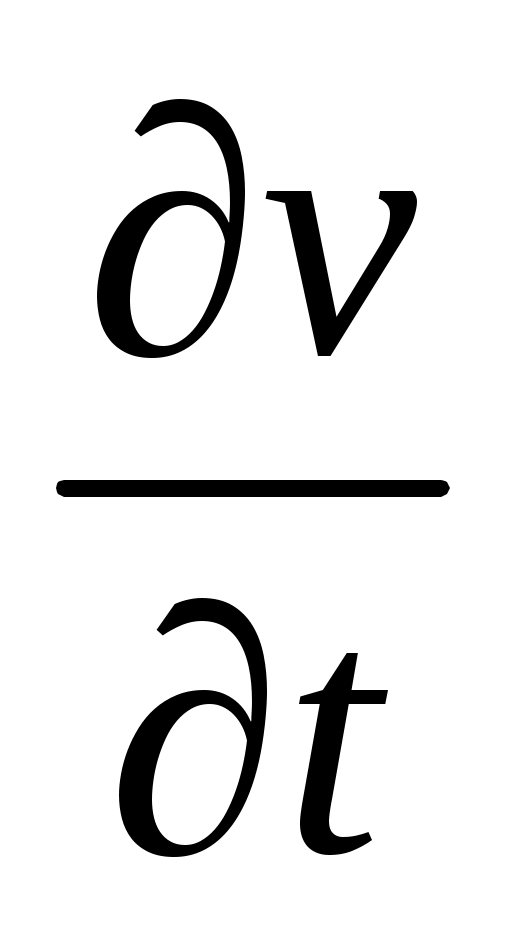 называется локальной, а остальные слагаемые правой части (2.7) – конвективными производными.
называется локальной, а остальные слагаемые правой части (2.7) – конвективными производными.
Производная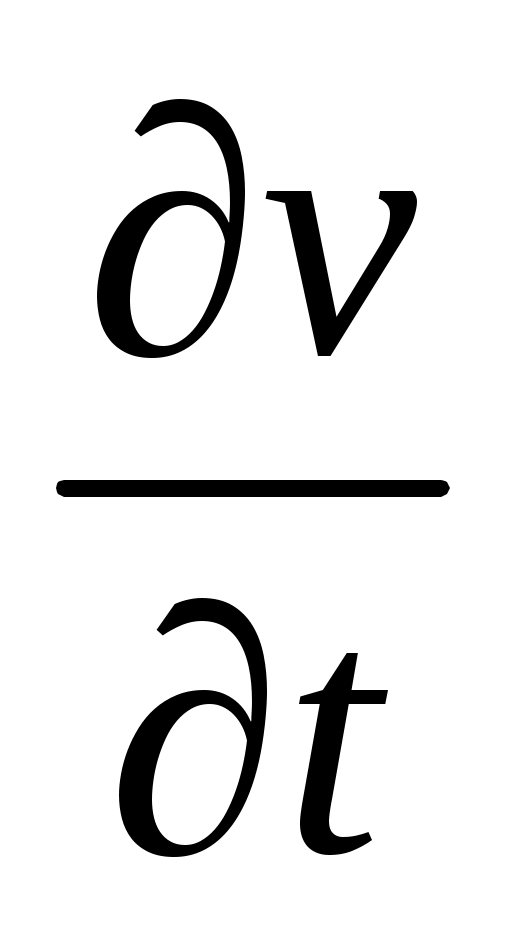 выражает изменение скорости движения частицы во времени при фиксированных координатах (точках). Величина этой производной отличается от нуля только при нестационарном течении. Все остальные слагаемые в правой части (2.7) соответствуют изменению скорости в пространстве и характеризуют неоднородность поля скоростей в данный момент времени.
выражает изменение скорости движения частицы во времени при фиксированных координатах (точках). Величина этой производной отличается от нуля только при нестационарном течении. Все остальные слагаемые в правой части (2.7) соответствуют изменению скорости в пространстве и характеризуют неоднородность поля скоростей в данный момент времени.
Для условий покоя жидкости правая часть уравнений (2.5) приравнивается нулю, т.к. компоненты ускорения ее элементов равны нулю, а сама система принимает вид:
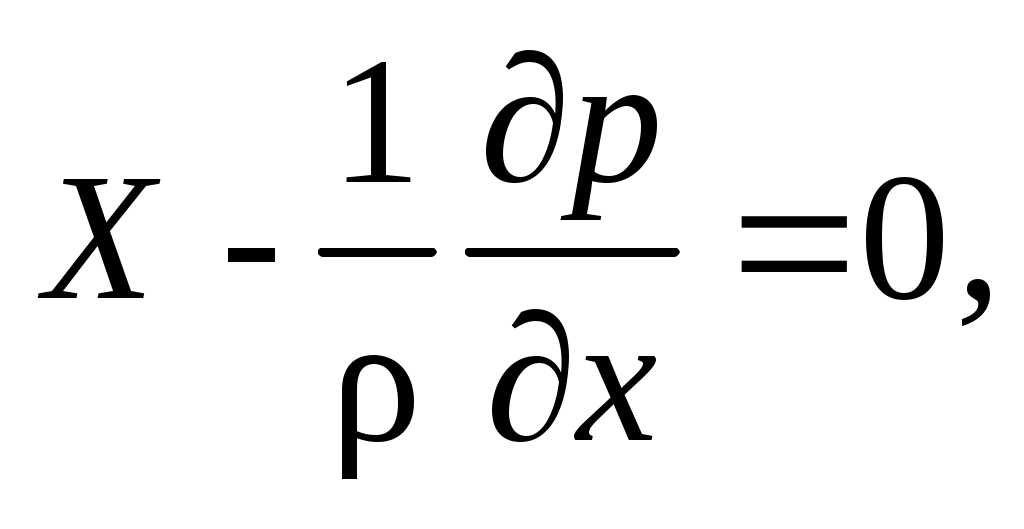
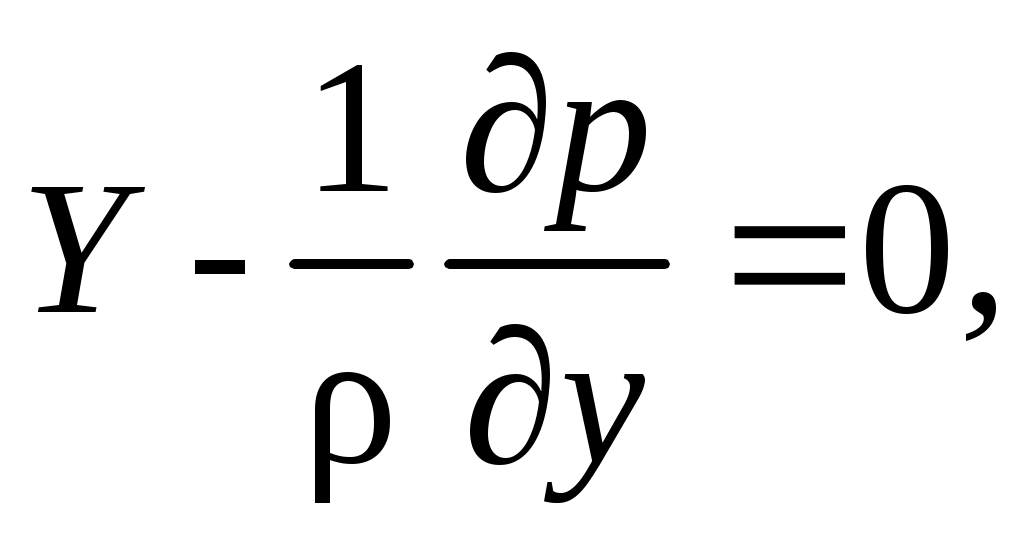 (2.8)
(2.8)
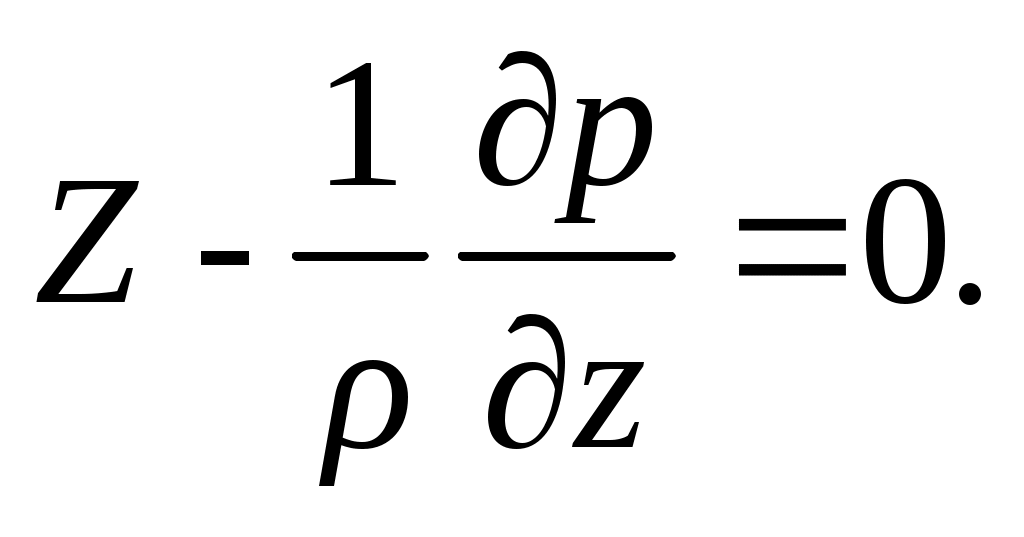
Уравнения (2.8) называются уравнениями гидростатики Эйлера. С помощью системы (2.8) решаются все основные задачи гидростатики для жидкости и газа.
Целью гидродинамического расчета является нахождение полей скоростей и давлений, т.е. в результате расчета должны быть найдены четыре величины:
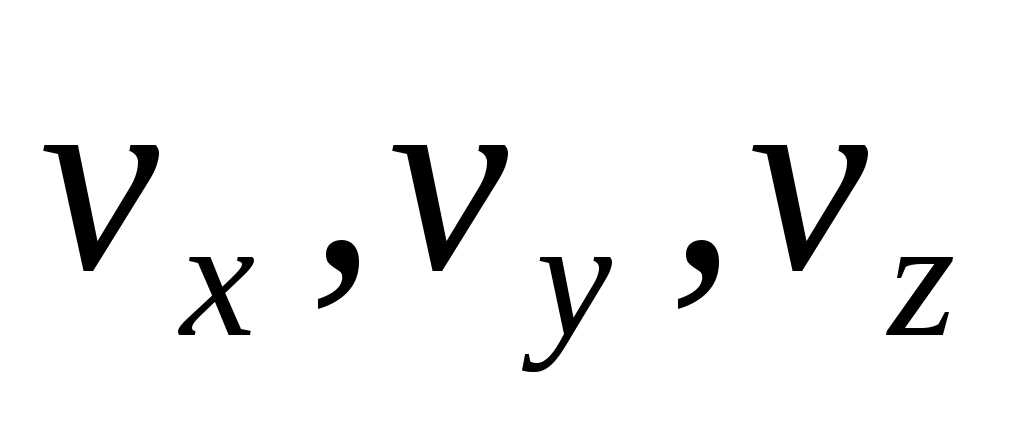 и . Принципиально это оказывается возможным, так как три уравнения Навье-Стокса (в проекциях) плюс уравнение неразрывности образуют замкнутую систему. Плотность и вязкость, входящие в них, считаются известными, а проекции массовых сил (X, Y, Z) задаются условиями конкретной задачи.
и . Принципиально это оказывается возможным, так как три уравнения Навье-Стокса (в проекциях) плюс уравнение неразрывности образуют замкнутую систему. Плотность и вязкость, входящие в них, считаются известными, а проекции массовых сил (X, Y, Z) задаются условиями конкретной задачи.
В проекциях на декартовы оси координат уравнение неразрывности записывается следующим образом:
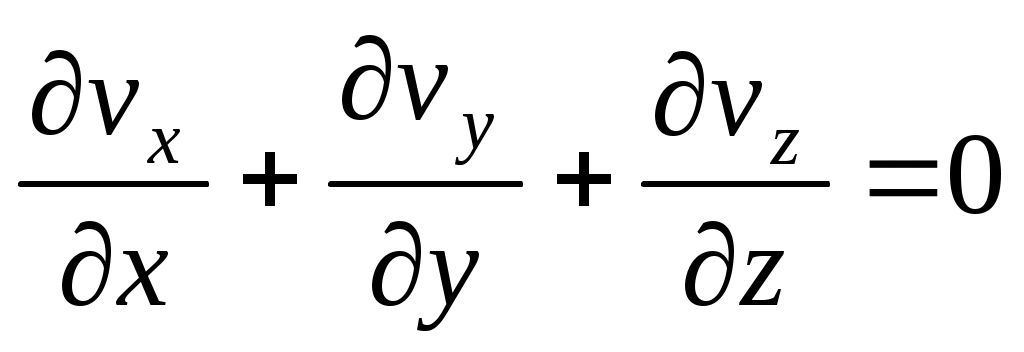 . (2.9)
. (2.9)
Установим физический смысл этого соотношения. Частные производные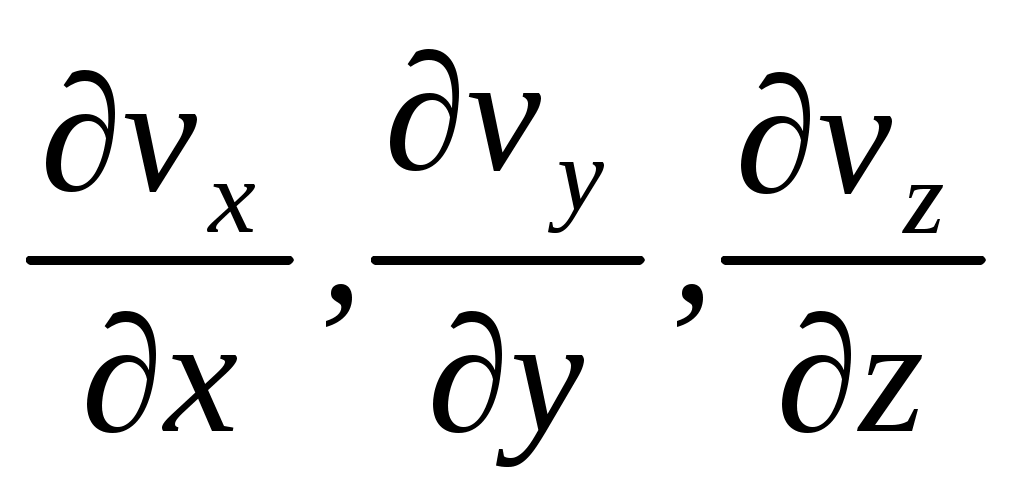 характеризуют скорость относительного удлинения (укорочения) жидкой частицы. Если этот процесс происходит одновременно вдоль всех координатных осей, то он приводит к объемному расширению либо сжатию частицы. Ясно, что если частица удлиняется вдоль осей x и y, то она должна укорачиваться относительно оси z. Другими словами, хотя бы одна из производных, входящих в уравнение неразрывности, должна быть отрицательна, т.к. в противном случае соотношение не может быть равным нулю.
характеризуют скорость относительного удлинения (укорочения) жидкой частицы. Если этот процесс происходит одновременно вдоль всех координатных осей, то он приводит к объемному расширению либо сжатию частицы. Ясно, что если частица удлиняется вдоль осей x и y, то она должна укорачиваться относительно оси z. Другими словами, хотя бы одна из производных, входящих в уравнение неразрывности, должна быть отрицательна, т.к. в противном случае соотношение не может быть равным нулю.
С чисто математических позиций уравнения Навье-Стокса относится к классу нелинейных дифференциальных уравнений в частных производных второго порядка. Одно из наиболее негативных из их свойств нелинейность, обусловленная наличием конвективных членов ускорения. Следует отметить, что до настоящего времени вследствие практически непреодолимых математических трудностей не получено ни одного общего решения уравнений Навье-Стокса в их полном виде, т.е. при сохранении всех конвективных членов и всех членов, учитывающих вязкость. Известны лишь отдельные частные решения.
Одним из основных граничных условий при интегрировании является условие «прилипания», т.е. равенство нулю скорости жидкости на стенке.
Прямое численное моделирование и моделирование крупных вихрей являются принципиально трехмерными подходами, поэтому использование двумерной формулировки задачи рассматривается как полезное с точки зрения сокращения затрат машинного времени, но необоснованное допущение.
При моделировании стационарных течений начальные условия не играют роли. Тем не менее их удачное задание позволяет сократить затраты машинного времени на получение статистически стационарного решения.
При решении полных уравнений Навье-Стокса требуется задание граничных условий на всех границах расчетной области.
На границе, через которую жидкость поступает в расчетную область, обычно задается распределение скорости, направление потока, распределения полного давления и полной температуры (или числа Маха), а также распределения характеристик турбулентности.
При решении задачи в неограниченной области из-за отсутствия точных граничных условий, заменяющих условия на бесконечности для исходной задачи с неограниченной областью, постановка граничных условий реализуется приближенным способом.
Для скорости на стенке используются граничные условия прилипания и непротекания (жесткие граничные условия). Для температуры задается температура стенки. При постановке граничных условий для характеристик турбулентности на стенке используется метод пристеночных функций.
2.2 Ламинарное движение в трубах
При рассмотрении уравнений движения вязкой жидкости (уравнений Навье-Стокса) отмечалось, что интегрирование их в большинстве случаев связано с непреодолимыми математическими трудностями. Однако известны и исключения. К числу их относится ламинарное течение между параллельными пластинами, одна из которых движется с какой-то скоростью u. Это так называемое течение Куэтта.
Рассмотрение закономерностей этого течения можно найти в оригинально построенном современном американском курсе прикладной гидродинамики [2, 9].
Другим примером является установившееся течение в круглой трубе, происходящее под действием постоянного перепада давлений – течение Пуазейля.
Профессор медицины Жан Пуазейль (1799-1869 гг.) во введении к своему трактату «Движение жидкостей в трубах малого диаметра» писал: «Я начал свои исследования потому, что прогресс в физиологии требовал определения законов движения жидкости в трубах малого диаметра (порядка 0,1 мм). Конечно, Дю Буа, Жирар, Навье и другие уже исследовали эти проблемы, однако они нуждаются в дальнейшем аналитическом и экспериментальном изучении, что было необходимо для надежного согласования теории с экспериментом». Опыты, выполненные Пуазейлем с трубкой диаметром 0,14 мм согласовывались с полученным им соотношением до тех пор, пока длина трубки составляла 51 мм; при уменьшении длины эта зависимость не соблюдалась. Этот факт и объясняется переходом от ламинарного к турбулентному режиму течения.
Как отмечалось выше, закономерности ламинарного течения в трубах можно получить путем прямого интегрирования уравнений Навье-Стокса. Решение задачи таким методом можно найти в [3].
В данном пособии используется другой способ, позволяющий получить более ясные физические представления.
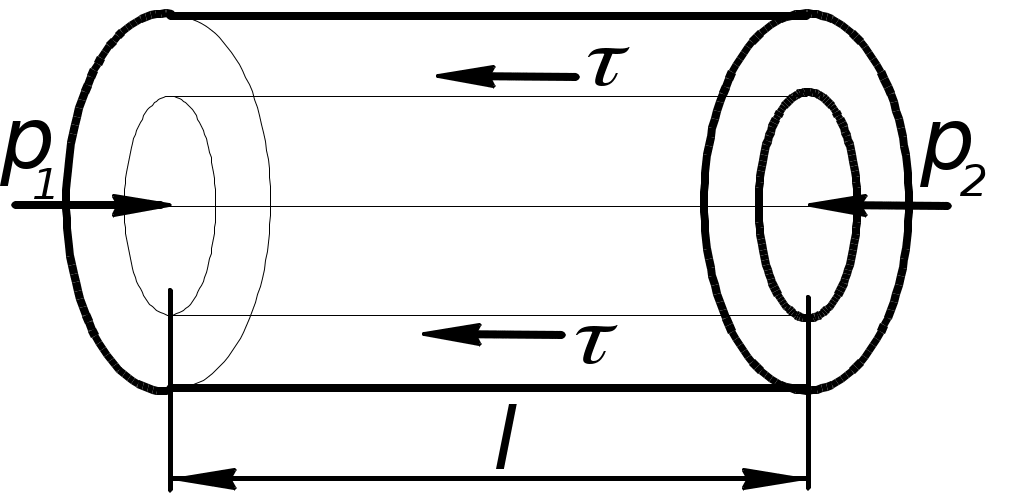
Рисунок 1.2 – Расчетная схема
Рассматриваем установившееся ламинарное течение в горизонтальной трубе (рисунок 1.2), происходящее под действием постоянного перепада давления. Радиус трубопровода – R.
Двумя сечениями, отстоящими на расстоянии l друг от друга, выделим отсек трубопровода, и в нем цилиндр радиуса r. Составим уравнение движения. Так как течение установившееся, то сумма проекций на ось всех сил, действующих на цилиндр, должна быть равна нулю. Другими словами, активные силы, приводящие частицы жидкости в движение, должны быть равны силам сопротивления.
Обозначим проекции ускорений массовых сил параллелепипеда на оси координат через X, Y и Z, а проекции ускорения движения его центра через
Эти соотношения называются уравнениями динамики сплошной среды в напряжениях.
Первое из полученных уравнений (2.1) можно привести к виду [15]:
Оставшиеся два уравнения преобразуются аналогично.
Для несжимаемой жидкости выражение в скобках в последнем члене этого соотношения равно нулю.
Воспользуемся значком
который называется оператором Лапласа.
Кроме того, после представления полной производной
В итоге, первое из равенств, а по аналогии с ним, и вся система (2.1) для несжимаемой жидкости примет вид
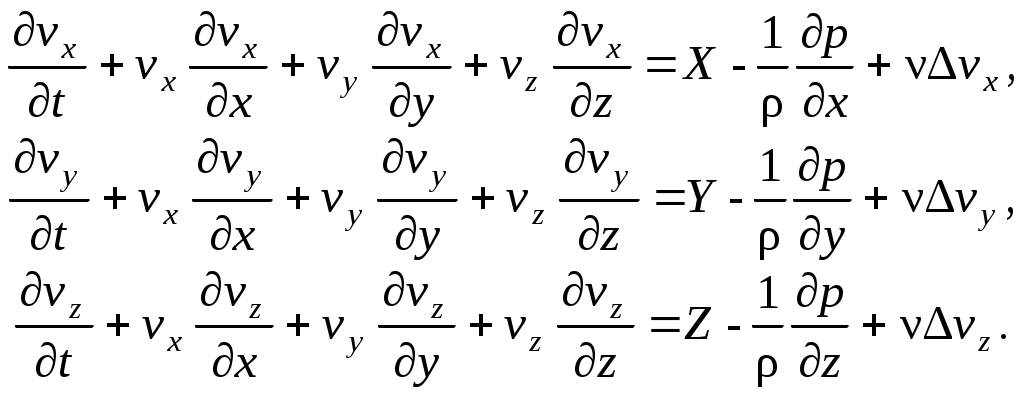
(2.4)
Равенства (2.4) называются уравнениями Навье – Стокса для жидкости. Для идеальной жидкости и газа (
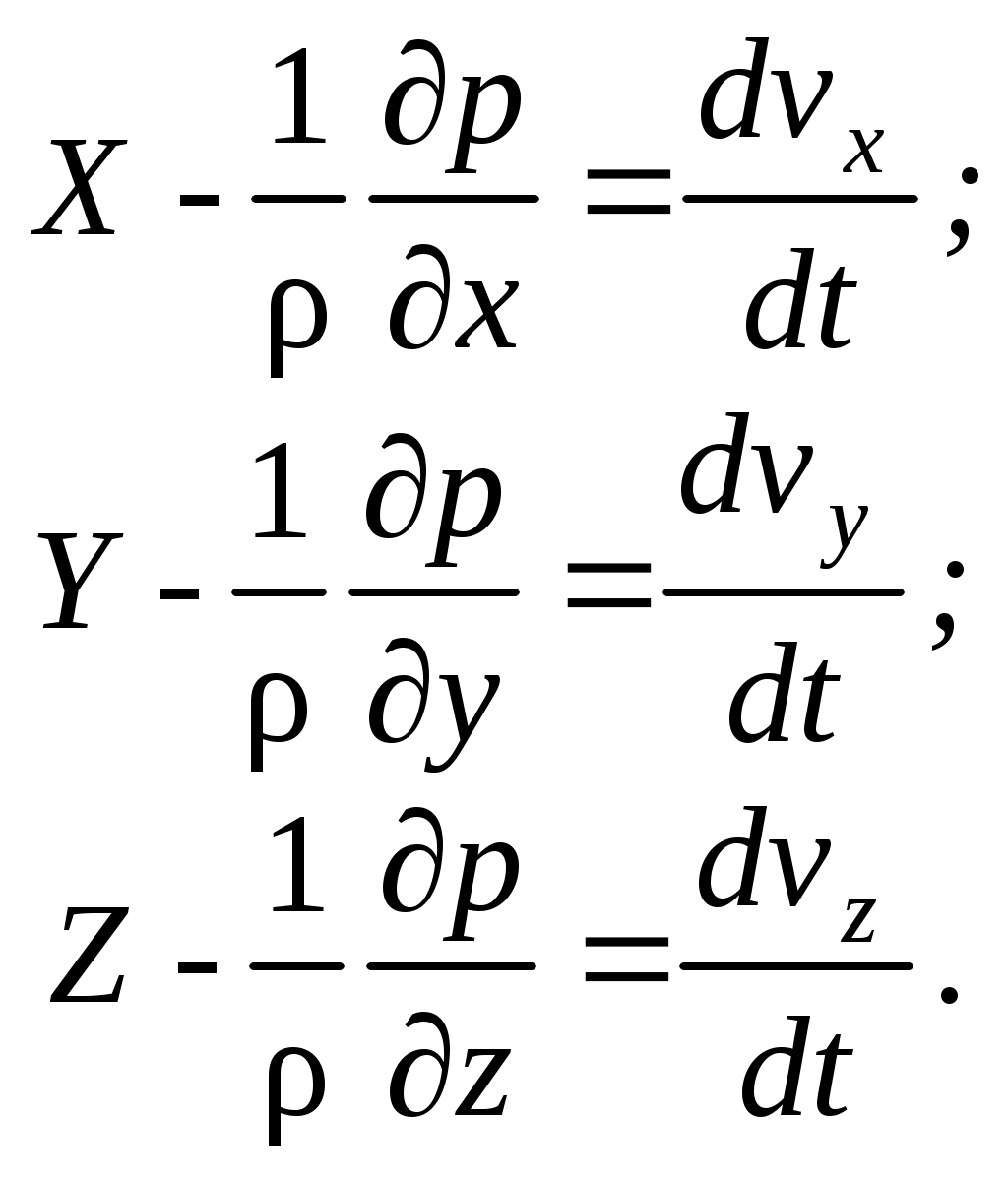 (2.5)
(2.5)Уравнения (2.5) называются гидродинамическими уравнениями Эйлера.
Система уравнений (2.5) может быть представлена в векторной форме
здесь w – ускорение массовых сил; p рассматривается как скалярная функция координат x, y, z, а gradp , как векторная функция x, y, z.
Кроме того выражение
представляющее собой полную производную скорости от времени в гидромеханике называется также индивидуальной или субстанциональной производной. Ее составляющая
Производная
Для условий покоя жидкости правая часть уравнений (2.5) приравнивается нулю, т.к. компоненты ускорения ее элементов равны нулю, а сама система принимает вид:
Уравнения (2.8) называются уравнениями гидростатики Эйлера. С помощью системы (2.8) решаются все основные задачи гидростатики для жидкости и газа.
Целью гидродинамического расчета является нахождение полей скоростей и давлений, т.е. в результате расчета должны быть найдены четыре величины:
В проекциях на декартовы оси координат уравнение неразрывности записывается следующим образом:
Установим физический смысл этого соотношения. Частные производные
С чисто математических позиций уравнения Навье-Стокса относится к классу нелинейных дифференциальных уравнений в частных производных второго порядка. Одно из наиболее негативных из их свойств нелинейность, обусловленная наличием конвективных членов ускорения. Следует отметить, что до настоящего времени вследствие практически непреодолимых математических трудностей не получено ни одного общего решения уравнений Навье-Стокса в их полном виде, т.е. при сохранении всех конвективных членов и всех членов, учитывающих вязкость. Известны лишь отдельные частные решения.
Одним из основных граничных условий при интегрировании является условие «прилипания», т.е. равенство нулю скорости жидкости на стенке.
Прямое численное моделирование и моделирование крупных вихрей являются принципиально трехмерными подходами, поэтому использование двумерной формулировки задачи рассматривается как полезное с точки зрения сокращения затрат машинного времени, но необоснованное допущение.
При моделировании стационарных течений начальные условия не играют роли. Тем не менее их удачное задание позволяет сократить затраты машинного времени на получение статистически стационарного решения.
При решении полных уравнений Навье-Стокса требуется задание граничных условий на всех границах расчетной области.
На границе, через которую жидкость поступает в расчетную область, обычно задается распределение скорости, направление потока, распределения полного давления и полной температуры (или числа Маха), а также распределения характеристик турбулентности.
При решении задачи в неограниченной области из-за отсутствия точных граничных условий, заменяющих условия на бесконечности для исходной задачи с неограниченной областью, постановка граничных условий реализуется приближенным способом.
Для скорости на стенке используются граничные условия прилипания и непротекания (жесткие граничные условия). Для температуры задается температура стенки. При постановке граничных условий для характеристик турбулентности на стенке используется метод пристеночных функций.
2.2 Ламинарное движение в трубах
При рассмотрении уравнений движения вязкой жидкости (уравнений Навье-Стокса) отмечалось, что интегрирование их в большинстве случаев связано с непреодолимыми математическими трудностями. Однако известны и исключения. К числу их относится ламинарное течение между параллельными пластинами, одна из которых движется с какой-то скоростью u. Это так называемое течение Куэтта.
Рассмотрение закономерностей этого течения можно найти в оригинально построенном современном американском курсе прикладной гидродинамики [2, 9].
Другим примером является установившееся течение в круглой трубе, происходящее под действием постоянного перепада давлений – течение Пуазейля.
Профессор медицины Жан Пуазейль (1799-1869 гг.) во введении к своему трактату «Движение жидкостей в трубах малого диаметра» писал: «Я начал свои исследования потому, что прогресс в физиологии требовал определения законов движения жидкости в трубах малого диаметра (порядка 0,1 мм). Конечно, Дю Буа, Жирар, Навье и другие уже исследовали эти проблемы, однако они нуждаются в дальнейшем аналитическом и экспериментальном изучении, что было необходимо для надежного согласования теории с экспериментом». Опыты, выполненные Пуазейлем с трубкой диаметром 0,14 мм согласовывались с полученным им соотношением до тех пор, пока длина трубки составляла 51 мм; при уменьшении длины эта зависимость не соблюдалась. Этот факт и объясняется переходом от ламинарного к турбулентному режиму течения.
Как отмечалось выше, закономерности ламинарного течения в трубах можно получить путем прямого интегрирования уравнений Навье-Стокса. Решение задачи таким методом можно найти в [3].
В данном пособии используется другой способ, позволяющий получить более ясные физические представления.

Рисунок 1.2 – Расчетная схема
Рассматриваем установившееся ламинарное течение в горизонтальной трубе (рисунок 1.2), происходящее под действием постоянного перепада давления. Радиус трубопровода – R.
Двумя сечениями, отстоящими на расстоянии l друг от друга, выделим отсек трубопровода, и в нем цилиндр радиуса r. Составим уравнение движения. Так как течение установившееся, то сумма проекций на ось всех сил, действующих на цилиндр, должна быть равна нулю. Другими словами, активные силы, приводящие частицы жидкости в движение, должны быть равны силам сопротивления.