Активные силы:

. (2.10)

Силы сопротивления:

. (2.11)

Таким образом:

(2.12)

и

. (2.13)

Из (2.13), в частности, следует, что касательные напряжения изменяются вдоль радиуса по линейному закону. С другой стороны, по Ньютону касательные напряжения:

. (2.14)

Знак «минус» потому, что направления отсчета y и r противоположны.

Приравнивая (2.13) и (2.14), получаем:

. (2.15)

Либо после разделения переменных:

(2.16)

и после интегрирования:

. (2.17)

Произвольную постоянную интегрирования находим из граничных условий: при и (условие прилипания), и .

Следовательно,

(2.18)

либо

(2.19)

Максимальная скорость движения частиц будет на оси трубы, т.е. при , а ее величина

. (2.20)

Подставляя (2.20) в (2.19) получим

. (2.21)

Из чего следует, что в поперечном сечении трубы скорости распределены по параболическому закону, т.е. эпюра скорости представляет собой параболоид вращения.

Выражение (2.21) можно представить в виде

. (2.22)

Из чего следует, что отношение скорости в любой точке к скорости на оси не зависит от расхода, рода жидкости и материала стенок трубы: при всех значениях

---

оно одинаково.

Определим расход, протекающий через трубопровод. При введении понятия о средней скорости было показано, что

, (2.23)

где – уравнение эпюры скорости.

Воспользуемся (2.18), что дает

. (2.24)

Выполнив интегрирование и имея в виду (2.20), можно получить

. (2.25)

Из чего следует, что

. (2.26)

Раскрывая значение по (2.20), получаем выражение для определения потерь давления при ламинарном режиме течения в круглой трубе:

. (2.27)

Либо, заменяя радиус диаметром:

. (2.28)

Полученное соотношение носит название формулы Хагена-Пуазейля. Для потерь напора с учетом того, что , формула принимает вид

. (2.29)

Важнейший вывод, следующий из этого соотношения, можно сформулировать так: потери давления (напора) при ламинарном течении в круглых трубах линейно зависят от средней скорости.

Выполним некоторые формальные преобразования формулы Хагена-Пуазейля, которые окажутся полезными в дальнейшем. Умножим числитель и знаменатель (2.29) на , что дает:

. (2.30)

Таким образом, можем записать, что в формуле при ламинарном течении .

2.3 Турбулентное течение жидкости

2.3.1 Общие сведения

---

Теория турбулентных течений представляет собой важнейший для практики, но и наиболее сложный раздел гидродинамики.

Первые серьезные исследования перехода к турбулентности были выполнены О. Рейнольдсом в 1883 году. Им же со ссылкой на Стокса был предложен ответ: «Общей причиной изменения стационарного течения на завихряющееся является то обстоятельство, что при некоторых условиях стационарное движение становится неустойчивым, так что бесконечно малые возмущения могут привести его к переходу в волнистое движение». «Волнистое движение», так первоначально было названо турбулентное движение Рейнольдсом. К сожалению, исследование бесконечно малых возмущений не дало критических значений, близких к наблюдавшимся в опытах.

Основной, определяющей чертой турбулентного движения является его хаотичность. Это означает, что скорость (и другие параметры) в любой точке потока зависят от времени. Более того, эти флуктуации скорости в данной точке также являются хаотическими.

Впервые гипотеза о физическом механизме турбулентного перемешивания была высказана английским ученым Л. Ричардсоном в 1922 г. Условно турбулентное движение принято рассматривать как совокупное движение отдельных структур, называемых молями либо вихрями, совершающими как поступательное, так и вращательное движение. По Ричардсону развитая турбулентность представляет собой иерархию «вихрей». При зарождении вихри имеют большие размеры, соизмеримые с размерами канала. Затем за счет потери устойчивости они распадаются на более мелкие, передавая при этом им свою энергию. Возникает каскадный процесс, в котором энергия осредненного потока последовательно передается вихрям все более мелких масштабов. В конечном итоге образуются вихри минимального масштаба, которые далее не разрушаются. При этом нижний размер вихря (турбулентного образования) определяется вязкостью среды. В самых малых вихрях кинетическая энергия турбулентности за счет сил вязкого трения превращается в тепло, т.е. происходит диссипация энергии. Это указывает на необратимый характер процесса.

Из сказанного ясно, что турбулентное движение по своей физической природе является движением неустановившимся. С другой стороны, непосредственные измерения свидетельствуют, что при турбулентном характере потока в нем можно выделить основную, так называемую регулярную часть, на которую накладывается случайная часть движения.

---

На рисунке 1.3 показан типичный вид экспериментально снятой зависимости проекции скорости в какой-то точке потока от времени при сохраняющихся неизменными граничных условиях.



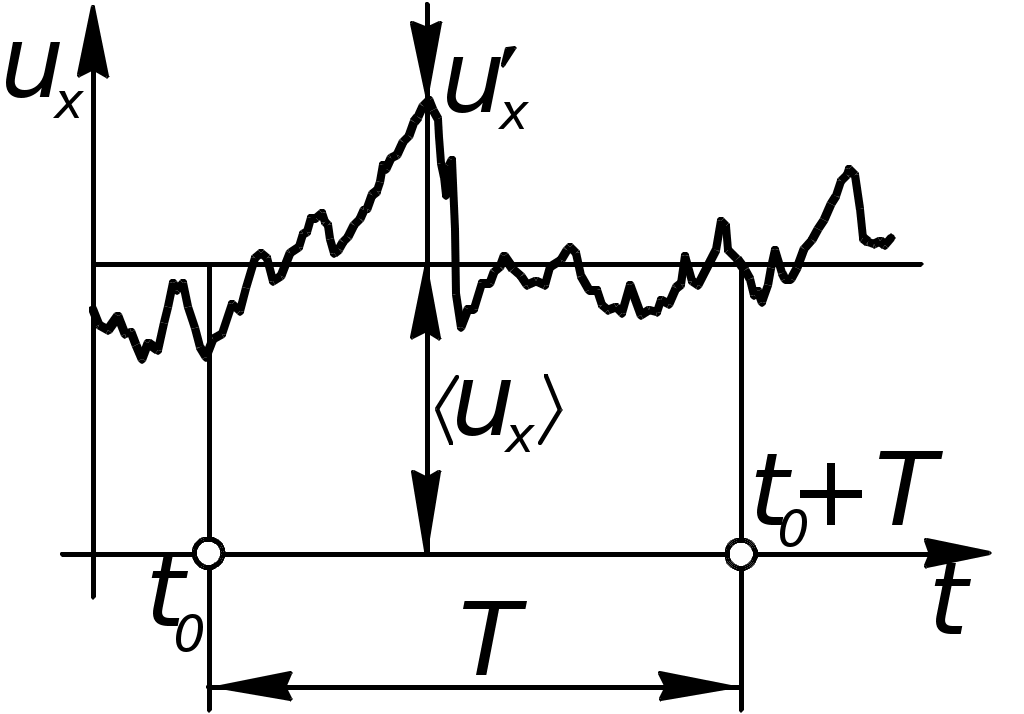
Рисунок 1.3 – Колебания скорости

Как следует из графика, особенностью этого процесса является его непериодичность, при этом:

, (2.31)

где – осредненная скорость, представляющая регулярную часть; – пульсационная скорость, разность между мгновенным и регулярным значением скорости.

Аналогичные соотношения можно записать и для других компонент.

Таким образом, осредненная скорость – это какое-то устойчивое значение, вокруг которого происходит изменение рассматриваемой проекции скорости (в данном случае). Все сказанное в равной мере относится и к другим параметрам, в частности, к давлению.

Наиболее важной характеристикой течения при его расчете является поле скоростей. Но, как показано выше, в любой точке потока при турбулентном течении скорость выступает как случайная величина, что исключает возможность записи начальных условий для системы дифференциальных уравнений Навье-Стокса, т.е. оказывается невозможной математическая постановка задачи. Именно это и приводит к необходимости перехода к какому-то осредненному описанию, использующему не истинные, а осредненные величины скоростей и давлений. Осреднение скоростей и давлений производится путем интегрирования функций , , , по промежутку времени T, величина которого намного больше так называемого характерного времени турбулентных пульсаций. Это время определяется как частное от деления масштаба l на скорость турбулентных пульсаций. Под масштабом турбулентных пульсаций понимают расстояние, на котором пульсации претерпевают заметное изменение. Так, например, при турбулентном движении в трубах наибольший масштаб пульсаций равен диаметру трубы. Таким образом, осредненная компонента скорости, например,

---

:

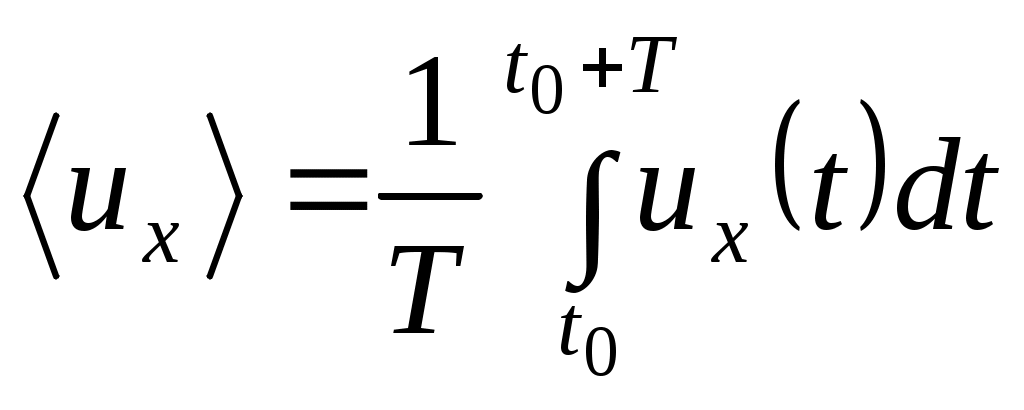(2.32)

Аналогичное соотношение можно записать и для давления. При этом, поскольку флуктуации (пульсации) имеют как положительный так и отрицательный знак, то:

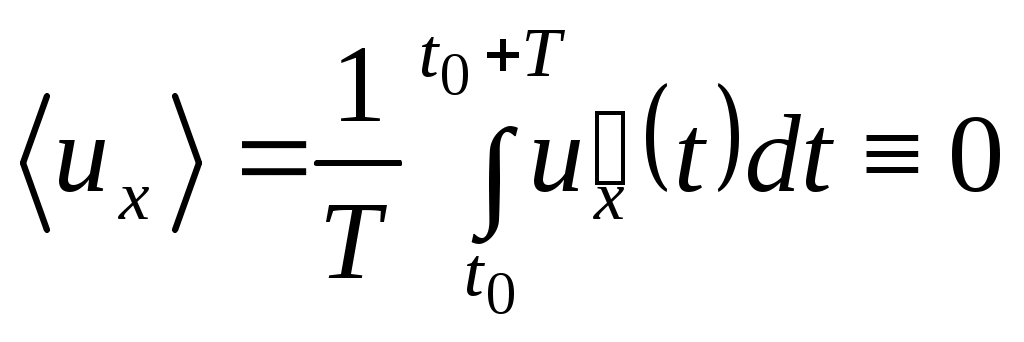(2.33)

Ясно также, что . Если в данной точке потока , то турбулентность называют изотропной, а если это условие соблюдается во всех точках, то она называется еще и однородной.
2.3.2 Уравнения Рейнольдса

Как уже отмечалось, сложность турбулентного движения делает невозможным строгое рассмотрение течений при заданных граничных условиях. Одной из возможных альтернатив является переход от истинной картины, детали которой нам неизвестны, к рассмотрению осредненного турбулентного течения, т.е., по существу, замена принципиально неустановившегося движения на квазиустановившееся. Этот переход был предложен О. Рейнольдсом. Суть его сводится к тому, что в уравнениях движения вязкой жидкости (уравнениях Навье-Стокса) и уравнении неразрывности истинные значения параметров по определенным правилам заменяются их осредненными значениями. Получаемая таким образом новая система уравнений носит название уравнений Рейнольдса. Описание данной системы можно найти в ряде учебных пособий [6].

Наиболее существенным результатом этой операции является то, что вследствие нелинейности уравнений Навье-Стокса в уравнениях Рейнольдса появляются дополнительные члены, которые получили название напряжений Рейнольдса. Для наиболее простого плоскопараллельного течения эти напряжения имеют вид:

, (2.34)

где угловые скобки – символ осреднения.

Таким образом, в осредненном турбулентном потоке к обычным вязкостным напряжениям добавляются напряжения, зависящие от пульсации скорости. Физически это объясняется тем, что между разными участками турбулентного потока происходит обмен количеством движения, обусловленный перемешиванием частиц. Перенос количества движения вызывает дополнительное торможение либо ускорение отдельных масс жидкости, т.е. приводит к возникновению турбулентных напряжений.

---

Смотрите также файлы

• Темы занятий.docx

• Химический факультет отчет по учебной практике.docx

• Разговор о важном 23 января 2023 г.docx

• Тема вкр Моделирование специальной физической подготовки в тренировочном процессе биатлонистов оглавление.docx

• Бортовые магнитофоны.pptx