Файл: Зертханалы жмыс 2 Пні Электр энергетикасындаы математикалы есептер жне компьютерлік модельдеу Таырыбы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 22
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«Әбілқас Сағынов атындағы Қарағанды техникалық университеті» КЕАҚ
ЭЖ кафедрасы
Зертханалық жұмыс № 2
Пәні: Электр энергетикасындағы математикалық есептер және компьютерлік модельдеу
Тақырыбы: КҮЙ КЕҢІСТІГІНДЕ СЫЗЫҚТЫ ЖӘНЕБЕЙСЫЗЫҚТЫЖҮЙЕЛЕРДІҢМАТЕМАТИКАЛЫҚМОДЕЛДЕРІНЗЕРТТЕУ
Орындаған: Абдрахман Нариман
Тобы: ЭЭ-21-2
Қабылдаған: Әбенова Ж.Б.
Қарағанды 2023

| MATLAB (Simulink) State-Space блогы: | MATLAB (Command Windows): >> A=[0 1;-a2 –a1] >> B=[0; b] >> c=[1 0] >> sf=ss(A,B,c,0) >> step(sf) % sf моделінің өтпелі сипаттамасын тұрғызу |
| Нұсқа № | 1 және 2 тапсырма | ||
| a1 | a2 | b | |
| 1 | 2 | 5 | 1 |
Біз ең бірінші Command Windows парағын ашып алып берілген функцияларды енгіземіз:
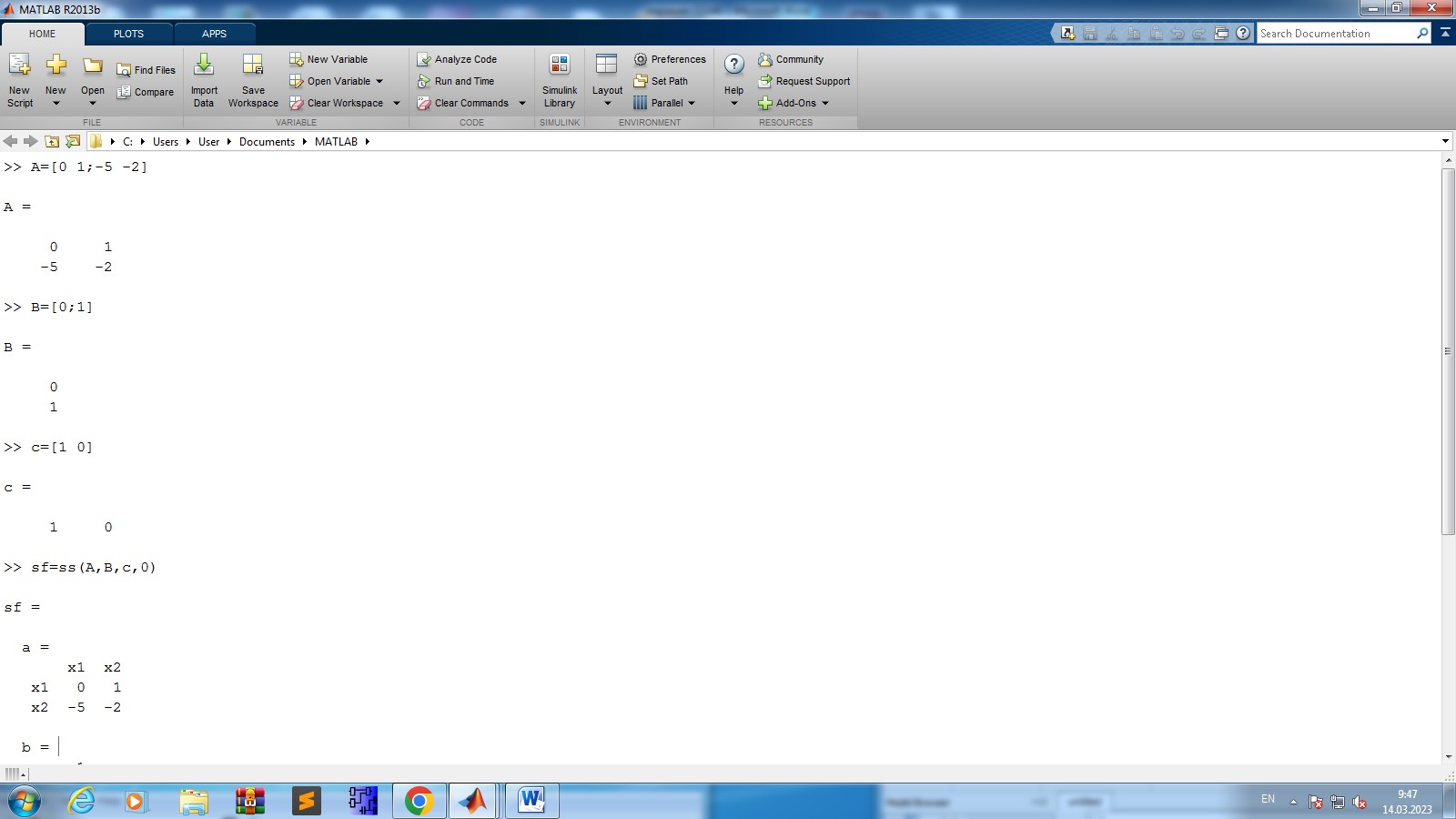
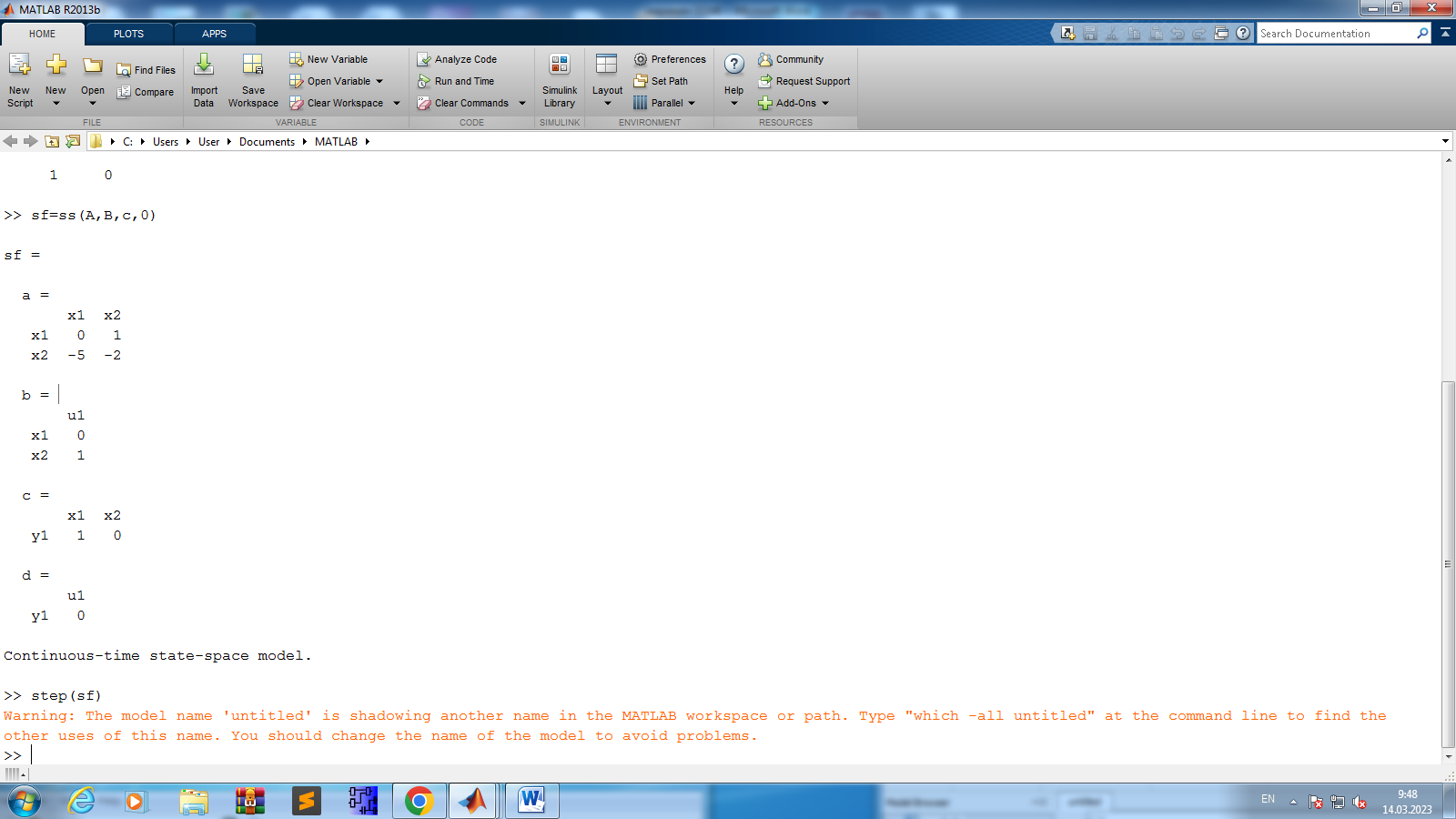
Осы функцияларды енгізгеннен кейін, Enter қосымшасын басу арқылы графикты шығардық:
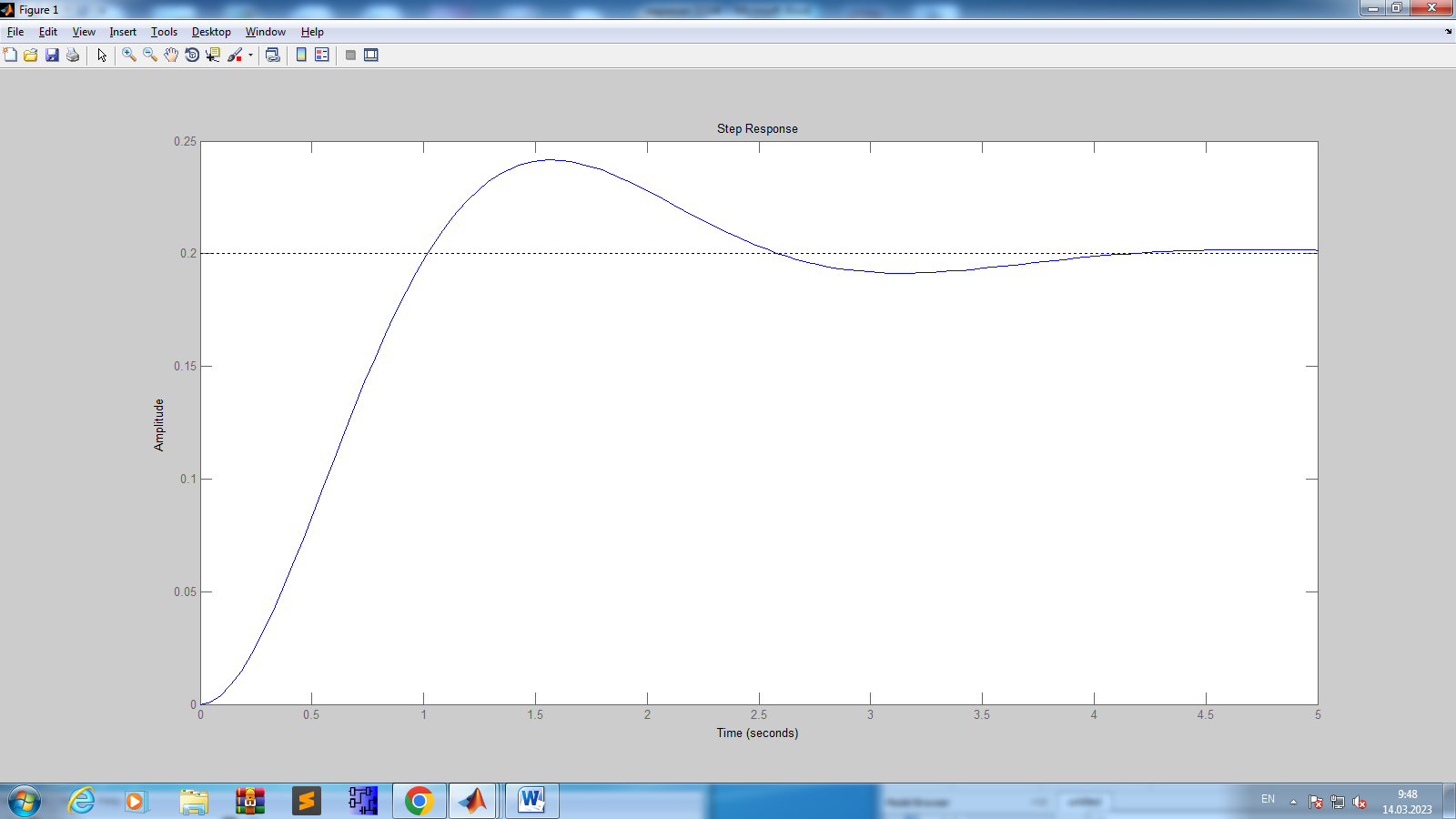
№2 зертханалық жұмыс бойынша бақылау сұрақтары
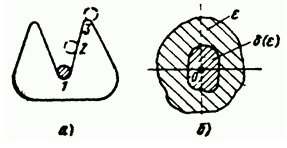
2. Жүйеніңүлкенжәнекішкенеаралығындаорнықтыөтпеліпроцестіңсуретіқандайболады?
«Кішкентайдағы» төзімділік пен «үлкендегі» төзімділік арасындағы айырмашылықты суреттің көмегімен көрсетуге болады. 17.1, а. Бұл суретте доп салынған шұңқыр көрсетілген. Егер сіз допты 1-позициядан 2-позицияға жылжитындай етіп итеріп, содан кейін оны өзіңізге қарай жіберсеңіз, онда ауырлық күшінің әсерінен доп өзінің бастапқы қалпына (теңдік күйі) оралады. Егер доп көбірек күшпен итерілсе, ол 3-позициядан өтіп, шұңқырдан шығады. Осылайша, жүйе (17.1, а-сурет) «кішіде» тұрақты және «үлкенде» тұрақсыз.
3. Күйлеркеңістігініңматематикалықмоделідегенімізне?
Күйлік-кеңістіктік модельдер жүйенің кіріс сигналын көрсетуін ғана емес, сонымен қатар оның ішкі құрылымын сипаттайтын модельдер болып табылады.
Ол үшін бір ғана математикалық сипаттаманы – күй айнымалысын пайдалану ыңғайлы.
4. Күйлер кеңістігінің математикалық моделдерінің түрлері?

5. Фазалық кеңістік. Фазалық портреттәсілі
Фазалық кеңістік – координат осьтерінің бойында динамикалық жүйенің күйін сипаттайтын айнымалылар сызылған кеңістік. Егер жүйенің қозғалысы n-ші ретті дифференциалдық теңдеумен сипатталса, онда бұл жүйенің күйін кез келген уақытта n-өлшемді фазалық кеңістіктің қандай да бір нүктесі арқылы сипаттауға болады, оның осьтерінің бойымен координаталарының бірі оның туындыларының жүйесі және (n-1) графигі салынған. Жүйенің күйін сипаттайтын нүкте бейнелеуші нүкте деп аталады.
Фазалық жазықтық әдісі екінші ретті жүйелерді зерттеу үшін қолданылады және жазықтықта фазалық портреттерді салудан тұрады. Ол үшін күй теңдеулерінен уақыт алынып тасталады және фазалық қисықтардың теңдеулері анықталады. Егер сызықты емес элементтің бөлшектік сызықтық сипаттамасы бар жүйе қарастырылса, мәселе өте қарапайым болады. Бұл жағдайда фазалық жазықтықтың әртүрлі аймақтарында жүйе сызықтық теңдеулер арқылы сипатталады, оларға сәйкес фазалық траекториялар құрастырылады, олар кейіннен сызықты емес сипаттама түрімен анықталған коммутациялық сызықтар бойымен «тігіледі».