6 (базовый уровень, время – 4 мин)

Тема: Определение возможных результатов работы простейших алгоритмов управления исполнителями и вычислительных алгоритмов

Что проверяется:

Ручное выполнение программ для исполнителей. Описание области, ограниченной ломаной линией, в виде набора условий.

1.7.2. Основные конструкции языка программирования. Система программирования.

1.1.4. Читать и отлаживать программы на языке программирования.

Что нужно знать и уметь:

• 
  выполнять ручную прокрутку программы для исполнителя, в которой используется цикл
  
• 
  строить на координатной плоскости фигуру, которую нарисует Черепаха (при ее известном начальном положении)
  

Пример задания:

Р-00 (Демо-2023). Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 7 [Вперёд 10 Направо 120]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Решение (теоретическое):

1. 
   так как при каждой итерации цикла Черепаха поворачивается на угол 120 (команда Направо 120), она будет рисовать правильный треугольник (за три итерации угол изменится ровно на 120 · 3 = 360, то есть, Черепаха вернётся в исходное положение)
   
2. 
   тело цикла выполняется 7 раз, то есть, Черепаха дважды обойдёт треугольник и пройдёт еще одну сторону; важно, что линия замкнётся
   
3. 
   перед выполнением программы Черепаха стоит в начале координат и смотрит вверх («на север»)
   
4. 
   теперь нужно нарисовать правильный треугольник со стороной 10 (команда Вперёд 10); это можно сделать, например, на листе в клеточку:
   

---

5. 
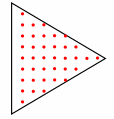
   Ответ: 38.
   

Проблема: при ручном построении можно неверно определить принадлежность точек, которые находятся близко к границе.

6. 
   для построения такого рисунка можно использовать, например, Word:
   

– добавить таблицу размером 10 на 10

– установить размер шрифта 1 и нулевые интервалы до и после абзаца

– установить одинаковые размеры ячейки, скажем, 0,5 см

– выбрать в меню Фигуры на вкладке Вставка равнобедренный треугольник, развернуть его вправо на 90 градусов и отрегулировать высоту так, чтобы она была равна 10 ячейкам; по правая вершина на рисунке должна иметь x-координату

7. 
   можно также использовать Excel, установив на вкладке Вид режим Разметка страницы: в этом режиме через меню Ячейки – Формат на вкладке Главная можно точно установить размеры ячейки в сантиметрах (Высота строки и Ширина столбца):
   

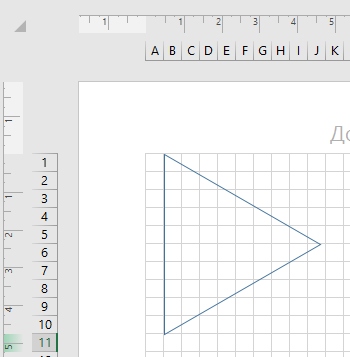
Решение (использование системы КуМир):

1. 
   https://www.youtube.com/watch?v=TTHospKjDvA (автор видео: А. Набережный)
   
2. 
   Ответ: 38.
   

Решение (перебор с помощью программы):

1. 
   для составления программы придётся построить систему условий, которая описывает область внутри контура
   
2. 
   уравнение правой границы треугольника: x = 0, нас интересует область x > 0
   
3. 
   верхняя граница: y = k₁·x + 10, нас интересует область y < k₁·x + 10
   

коэффициент

4. 
   нижняя граница: y = k₂·x, нас интересует область y > k₂·x
   

коэффициент

5. 
   организуем цикл, в котором перебираем значения x от 1 до 9 (можно и больше!) и значения y от 1 до 9; для каждой пары (x, y) проверяем два условия (третье, x > 0, уже выполнено автоматически за счёт выбранного диапазона изменения x); если оба условия выполнены, увеличиваем счётчик count:
   

count = 0

for x in range(1,10):

for y in range(1,10):

if y < -x/3**0.5+10 and y > x/3**0.5:

count += 1

print( count )

6. 
   Ответ: 38.
   
7. 
   вариант программы (сначала строится массив из всех пар координат точек, попавших внутрь области, затем выводится длина этого массива):
   

---

points = [ (x,y) for x in range(1,10) for y in range(1,10)

if y < -x/3**0.5+10 and y > x/3**0.5 ]

print( len(points) )

8. 
   решение-однострочник (без массива points):
   

print( len( [ (x,y) for x in range(1,10) for y in range(1,10)

if y < -x/3**0.5+10 and y > x/3**0.5 ] ) )

Решение (использование модуля turtle в Python, А. Неверов):

1. 
   в Python есть стандартный модуль turtle, в котором реализована «черепашья графика»; его можно использовать для того, чтобы построить заданную фигуру:
   

import turtle as t

k = 30 # масштаб

t.left( 90 ) # развернуть Черепаху "на север"

for i in range(7):

t.forward( 10*k )

t.right( 120 )

здесь переменная k задает масштаб – длину единичного отрезка на плоскости в пикселях

2. 
   далее нужно поставить точки с целочисленными координатами, для этого используется метод .dot (точка):
   

t.up() # «подними перо»

for x in range(0, 11):

for y in range(0, 11):

t.goto( x*k, y*k ) # в точку с заданными координатами

t.dot( 4 ) # ставим точку

диапазон при вызове функции range определяет область, которая заполняется точками; его нужно скорректировать, если точками покрыта не вся фигура

3. 
   приведём полную программу:
   

import turtle as t

k = 30 # масштаб

t.left( 90 ) # развернуть Черепаху "на север"

for i in range(7):

t.forward( 10*k )

t.right( 120 )

t.up()

for x in range(0, 11):

for y in range(0, 11):

t.goto( x*k, y*k )

t.dot( 4 )

4. 
   результат работы программы:
   

5. 
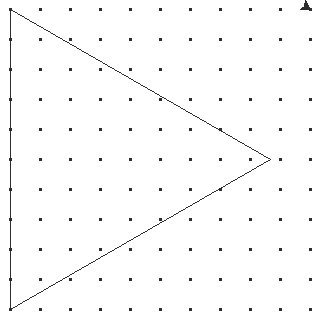
   подсчёт точек с целочисленными координатами, оказавшихся внутри контура, проводится визуально.
   

Решение (перебор с помощью программы, Б.С. Михлин):

1. 
   для вычисления угла наклона прямых, ограничивающих область, можно использовать функции модуля math: перевести угол в радианы и найти его тангенс:
   

from math import tan, radians

count = 0

k = tan(radians(30)) # tg угла 30 градусов

for x in range(1, 11):

for y in range(1, 11):

if y < -k * x + 10 and y > k * x:

count += 1

print(count) # Ответ 38

2. 
   Ответ: 38.
   

Решение (перебор с помощью программы + модуль turtle, Б.С. Михлин):

1. 
   полная программа:
   

---

from turtle import *

from math import *

tracer(2) # speed(0) команды ускорения рисования

hideturtle() # ht() скрыть изображение черепашки

m = 25 # масштаб

left(90) # lt(90)

for i in range(7):

forward(10 * m) # fd(10*m)

right(120) # rt(120)

penup() # up() поднять перо Черепашки

count = 0 # количество точек, попавших внутрь треугольника

k = tan(pi / 6) # тангенс угла пи/6 радиан (угла 30 градусов)

for x in range(0, 11):

for y in range(0, 11):

goto(x * m, y * m)

if (y < -k * x + 10 # ниже верхней линии треугольника?

and y > k * x # выше нижней линии треугольника?

and x > 0): # правее вертикальной линии треугольника?

dot(5, 'red') # красная точка (точка попала

# внутрь треугольника)

count += 1

else:

dot(5, 'black') # черная точка (точка не попала

# внутрь треугольника)

color('red')

write(count) # количество красных точек по колонкам

# нарастающим итогом

mainloop() # done()

2. 
   Ответ: 38.
   

---

Задачи для тренировки:

1. 
   Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
   

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 10 [Вперёд 6 Направо 120]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

2. 
   Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
   

Повтори k [Команда1 Команда2 … КомандаS]

означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 15 [Вперёд 15 Направо 120]

Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

---

Смотрите также файлы

• Введении в философию.docx

• Сколько однозначных чисел ты знаешь Сколько однозначных чисел ты знаешь.docx

• Профессиональное образовательное учреждение.pdf

• Вопросы Социальная динамика или концепция общественного прогресса О. Конта.docx

• Аннотация к рабочей программе по информатике для 9 классов.docx