Файл: Исследование связей двумерными непараметрическими методами с применением коэффициентов корреляции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 17
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа 4
Двумерные непараметрические методы
Цель работы: Исследование связей двумерными непараметрическими методами с применением коэффициентов корреляции.
Задание 1. В таблице приведены ранги объектов Х, У. Найти выборочный коэффициент ранговой корреляции Спирмена и Кендалла и при уровне значимости = 0,05 проверить гипотезу об отсутствии ранговой корреляции.
Вариант 3
| Х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| У | 2 | 7 | 3 | 10 | 5 | 9 | 1 | 8 | 4 | 6 |
Решение:
Выборочный коэффициент ранговой корреляции Спирмена Rs определим по формуле
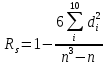
где d- разность между рангами по двум переменным
Найдем ранги Y. Для чего сначала расположим данные Y в убывающем порядке и пронумеруем их:
Определены критические значения.
| Значения Х | Ранг Х dx | Значения Y | Ранг Y, dy | d (ранг X - ранг Y) | d2 |
| 1 | 1 | 2 | 2 | -1 | 1 |
| 2 | 2 | 7 | 7 | -5 | 25 |
| 3 | 3 | 3 | 3 | 0 | 0 |
| 4 | 4 | 10 | 10 | -6 | 36 |
| 5 | 5 | 5 | 5 | 0 | 0 |
| 6 | 6 | 9 | 9 | -3 | 9 |
| 7 | 7 | 1 | 1 | 6 | 36 |
| 8 | 8 | 8 | 8 | 0 | 0 |
| 9 | 9 | 4 | 4 | 5 | 25 |
| 10 | 10 | 6 | 6 | 4 | 16 |
| | 55 | | 55 | | 148 |
Рассчитаем эмпирическое значение
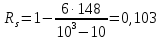
Критические значения для N = 10 при α=0,05, rкрит =0,64
Так как rs < rкрит, корреляция между X и Y не достигает уровня статистической значимости.
Рассчитаем коэффициент ранговой корреляции Кендалла.
Ранги факторного признака располагаются строго в порядке возрастания и параллельно записываются соответствующие им ранги результативного признака. Для каждого ранга из числа следующих за ним рангов подсчитывается количество больших него по величине рангов (заносится в столбец Р) и число рангов, меньших по значению (заносится в столбец Q).
В ряду Y справа от 2 расположено 8 рангов, превосходящих 2, следовательно, 2 породит в Р слагаемое 8.
Справа от 2 стоят 7 ранга, превосходящих 3 (это 10, 9, 8), т.е. в Р войдет 7 и т.д. В итоге Р = 22 и с использованием формул имеем:
| X | Y | ранг X, dx | ранг Y, dy | P | Q |
| 1 | 2 | 1 | 2 | 8 | 1 |
| 2 | 7 | 2 | 7 | 3 | 5 |
| 3 | 3 | 3 | 3 | 6 | 1 |
| 4 | 10 | 4 | 10 | 0 | 6 |
| 5 | 5 | 5 | 5 | 3 | 2 |
| 6 | 9 | 6 | 9 | 0 | 4 |
| 7 | 1 | 7 | 1 | 3 | 0 |
| 8 | 8 | 8 | 8 | 0 | 2 |
| 9 | 4 | 9 | 4 | 1 | 0 |
| 10 | 6 | 10 | 6 | 0 | 0 |
| | | | | 24 | 21 |
Корреляция Кендалла — это разность вероятностей «совпадений» и «инверсий»:
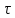 =
=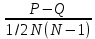
τ=
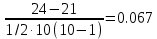
По таблице Лапласа находим zkp = 1.96
Так как |τ| < Tkp — нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима.
Задание 2. Шесть пар участников соревнования по фигурному катанию на льду оценивались двумя членами жюри. В результате этой оценки у каждого члена жюри пара получала определенное место. Необходимо проверить с заданным уровнем значимости = 0,05 нулевую гипотезу Н0 : W = 0 об отсутствии согласованности оценок членов жюри. Результаты оценок приведены в таблицах.
Вариант 3
| Член жюри | Номер пары | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 1 | 2 | 3 | 5 | 4 | 6 |
Решение:
1. Создание экспертной комиссии.
Число факторов n = 6, Число экспертов m = 2
2. Сбор мнений специалистов путем анкетного опроса.
Оценку степени значимости параметров эксперты производят путем присвоения им рангового номера. Фактору, которому эксперт дает наивысшую оценку, присваивается ранг 1. Если эксперт признает несколько факторов равнозначными, то им присваивается одинаковый ранговый номер. На основе данных анкетного опроса составляется сводная матрица рангов.
3. Составление сводной матрицы рангов.
| № п.п. / Эксперты | 1 | 2 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 5 |
| 5 | 5 | 4 |
| 6 | 6 | 6 |
Матрица рангов
| Факторы / Эксперты | 1 | 2 | Сумма рангов | d | d2 |
| x1 | 1 | 1 | 2 | (2-7)= -5 | 25 |
| x2 | 2 | 2 | 4 | (4-7)= -3 | 9 |
| x3 | 3 | 3 | 6 | 6-7=-1 | 1 |
| x4 | 4 | 5 | 9 | 9-7=2 | 4 |
| x5 | 5 | 4 | 9 | 9-7=2 | 4 |
| x6 | 6 | 6 | 12 | 12-7=5 | 25 |
| ∑ | 21 | 21 | 42 | | 68 |
где
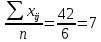
4. Оценка средней степени согласованности мнений всех экспертов.
Коэффициент конкордации:
где S = 68, n = 6, m = 2
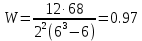
W = 0,97 говорит о наличии высокой степени согласованности мнений экспертов.
Выводы:
В работе рассчитали коэффициент ранговой корреляции Спирмена и Кендалла, с целью статистического изучения связи между явлениями. Ранговая корреляционная связь между признаками незначима.
Также проверили нулевую гипотезу, которая показывает наличие высокой степени согласованности мнений экспертов.
.