Файл: Решение задач Заключение Список использованных источников Введение Уравнения. Можно утверждать наверняка, что не найдется ни одного человека, который бы не был знаком с ними. Дети сызмала начинают решать задачи с иксом.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 70
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Два других корня,
1.4 Тригонометрическая формула Виета
Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
Очевидно, что любое кубическое уравнение можно привести к уравнению вида (4), просто поделив его на коэффициент a. Итак, алгоритм применения этой формулы:
. Вычисляем
2. Вычисляем
3. а) Если
И наше уравнение имеет 3 корня (вещественных):
б) Если
Вычисляем
Тогда единственный корень(вещественный):
Мнимые корни:
где:
В) Если
2. Решение задач
Пример 1. Найти действительные корни кубического уравнения
Решение:
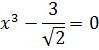
Применяем формулу сокращенного умножения разность кубов:
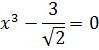
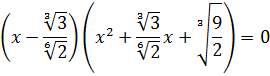
Из первой скобки находим
Ответ:
Пример 2. Решить уравнение
Решение:
Это уравнение возвратное. Проведем группировку:
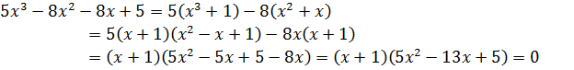
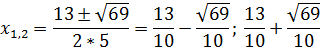
Пример 3. Найти корни кубического уравнения
Решение:
Преобразуем уравнение к приведенному: домножим на
Свободный член равен 36. Запишем все его делители:
Подставляем их по очереди в равенство
Таким образом,
Разделим
| | Коэффициенты многочлена | |||
| | 2 | -11 | 12 | 9 |
| -0.5 | 2 | -11+2*(-0.5)=-12 | 12-12*(-0.5)=18 | 9+18*(-0.5)=0 |
Получаем
Найдем корни квадратного трехчлена
Очевидно, что
Ответ:
Пример 4.Найти действительные корни уравнения
Решение:
Так как дискриминант
Ответ:
Пример 5. Найти корни кубического уравнения 2
Решение:
Имеем
Находим
Следовательно,
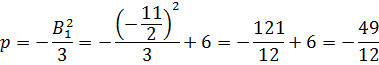
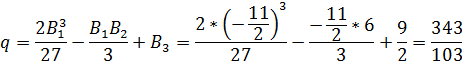
Подставляем в формулу Кардано: