Открытый урок по алгебре в 9 «А» классеОткрытый урок по алгебре в 9 классе:  «Решение неравенств второй степени». Цели и задачи: Образовательные: систематизировать материал по данной теме, закрепить умения и навыки и решения неравенств  второй степени с одной переменной; проведение диагностики усвоения системы знаний и умений, ее применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень. Коррекционно-развивающие: отработка внимательности и точности при выполнении заданий; развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность; выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно ее оценивать. Воспитательные: воспитание интереса к предмету через игровые моменты урока, занимательные задачи; воспитание культуры мышления, культуры речи, культуры поведения; воспитание сознательной дисциплины, понимания важности и значимости науки. Ход урока. 

1. 
   Организационный момент.
   

Здравствуйте, ребята. На предыдущих уроках мы свами начали изучать тему «Решение неравенств второй степени», узнали алгоритм решения неравенств. Эта тема очень важна, она является ступенькой для дальнейшего обучения, а также для успешной сдачи ГИА.Сегодня мы продолжим учиться решать такие неравенства.Представим себе, что сегодня наш класс – научно-исследовательский институт (сл.1).А вы, ученики, - сотрудники этого института. А именно, сотрудники различных лабораторий по проблемам математики, а именно: лаборатории теоретиков, лаборатории исследований, лаборатории эрудитов, лаборатории раскрытия тайн. Вас всех пригласили принять участие в заседании ученого совета, чтобы обсудить тему «Решение неравенств второй степени». В процессе работы вы должны: закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятых ранее моментах, проконтролировать и оценить свои знания. У каждого из вас на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце оцените свою работу как сотрудники наших лабораторий. 

---

Оценочный лист.                            Фамилия, имя­­­­­­_____________________________

Лаборатория теоретиков (максимум 5 балла)	Лаборатория исследований (максимум 4 баллов)	Лаборатория эрудитов (максимум 2 балла)	Лаборатория раскрытия тайн (максимум 5 баллов)	Активность на уроке (максимум 5 баллов)	Всего баллов	Оценка

Оценка «5»: 20-21 балловОценка «4»: 14-19 балловОценка «3»: ниже 14 балловДевизом нашего заседания является лозунг: «Дорогу осилит идущий, а математику мыслящий» (сл.2).А сейчас открываем тетради и запишем тему урока.«Решение неравенств». 1.     Актуализация опорных знаний.Итак, «Лаборатория теоретиков» (сл.3).Это наша первая лаборатория. В ней вы должны вспомнить теоретический материал по теме, который пригодиться вам в дальнейшей работе в других лабораториях. Посмотрите на карточку «Лаборатория теоретиков». Вам необходимо ответить на вопросы или продолжить предложения:

1. 
   Какое название имеет неравенство второй степени? (квадратное)
   
2. 
   Как называется процесс получения корней квадратного уравнения? (решение)
   
3. 
   Как называется последовательность действий при решении неравенства? (алгоритм)
   
4. 
   От чего зависит количество корней квадратного уравнения? (от дискриминанта)
   
5. 
   Если дискриминант квадратного уравнения больше нуля, то уравнение имеет …..корня. (два)
   
6. 
   Если дискриминант квадратного уравнения равен нулю, то уравнение имеет …..корень (один)
   
7. 
   Как называется число в неравенстве, стоящее перед переменной? (коэффициент)
   
8. 
       Графиком функции у= ах²+вх+с (а˃0) является (парабола, ветви которой направлены вверх).
   
9. 
       Графиком функции у= ах²+вх+с (а≤0) является (парабола, ветви которой направлены вниз)
   
10. 
    Неравенство вида (х-а)(х+в)(х-с)≤0 решается (методом интервалов)
    

Внимание: ответ должен быть полным и не забывайте про активность на уроке.Молодцы! Оцените свою работу в лаборатории теоретиков по 5-и бальной системе.

---

 Лаборатория теоретиков была пропуском в следующую лабораторию, которая называется «Лаборатория исследований» (сл.4)Выберите листок с таким названием. Вы видите 4 неравенств с решениями, среди которых есть верные, но есть и неверные. Вам надо исследовать эти решения на наличие ошибки. Если решение верное, то напротив него вы должны записать слово «верно», если же в решении ошибка, то вы записываете слово «неверно» и пишите верный результат.   Верно – неверно?

1)   х2 - 2х - 8˃0	х2 - 2х - 8=0    х1+х2=-2        х1= -2    х1∙х2= -8        х2= -4
2) -10х2+9х≤0	-10х2+9х=0               Д=в2 – 4ас                Д=144
3) (х-7)(х+2)(х-18)≤0	(х-7)(х+2)(х-18)=0 произведение=0, когда х=7 или  х=-2 или х=18

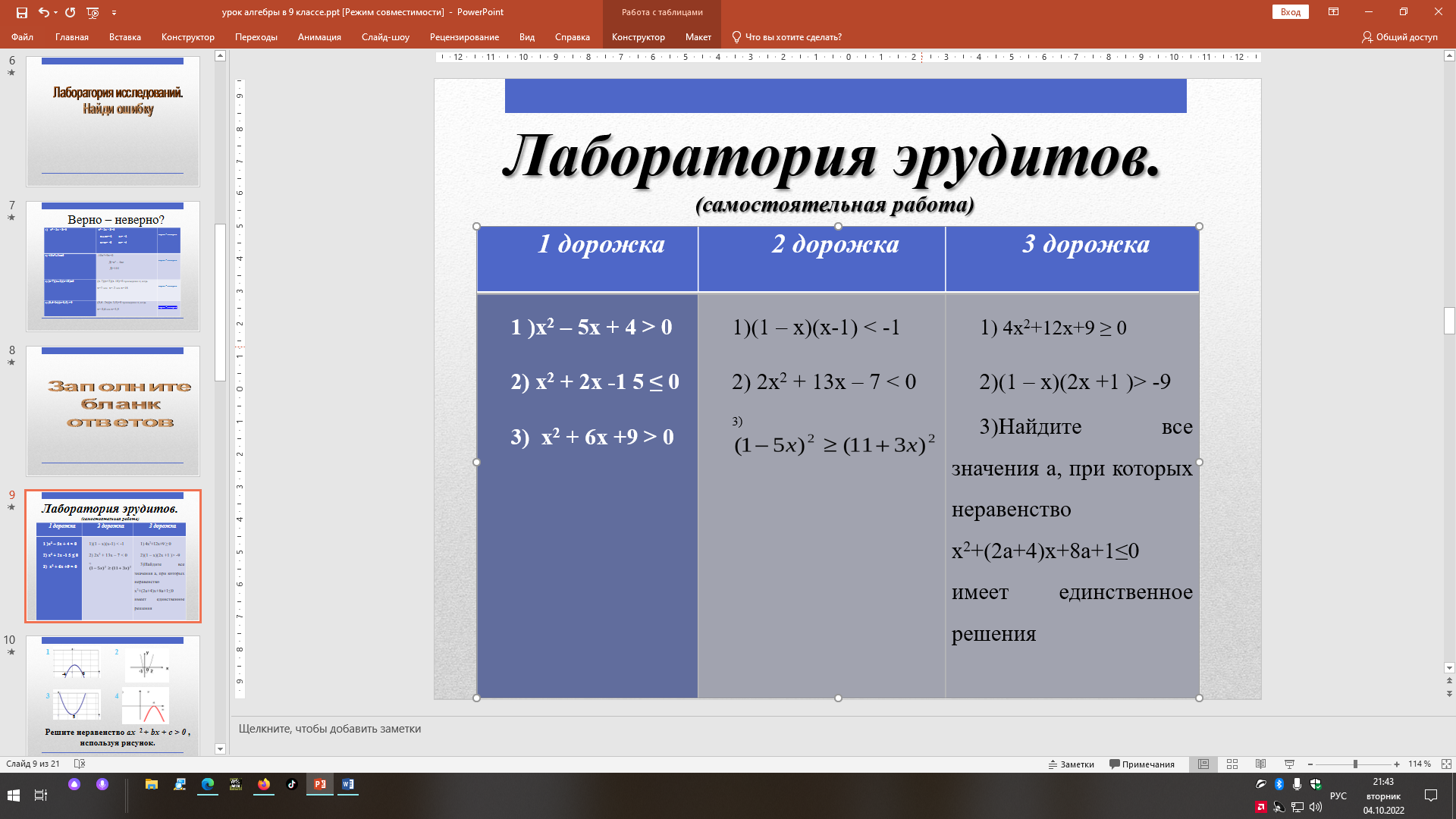
Проверяем правильные ответы разбираем ошибку, если она есть.В оценочный лист ставите количество баллов соответствующее числу правильных ответов (т.е. высшая оценка-4 балла). Закончив исследования, мы переходим в следующую лабораторию «Лабораторию эрудитов»(сл.5). Работая в этой лаборатории, будьте очень внимательны.                        В оценочный лист ставите баллы, соответствующие числу правильных ответов.Перед вами самая сложная лаборатория«Лаборатория раскрытия тайн»,требующая от вас умения правильно применить свои знания. Работа с учебником с.92 №334 (а) -1 ученик у доски.3.     Гимнастика для ума.Мы с вами поработали во всех лабораториях, а теперь немного отдохнем и посмотрим некоторые математические фокусы.Есть много математических фокусов. Но самым элегантным математическим фокусом является возведение в квадрат чисел, оканчивающихся цифрой 5.Проведем соответствующие рассуждения для числа 85 .85² = 7225Как быстро получить такой результат? Заметим, что достаточно 8 умножить на следующее за ним натуральное число 9, и мы получим 72, т.е. первые две цифры результата. Теперь достаточно приписать к полученному числу 25 и получается 7225, а это и есть ответ.

---

Проведем такую же операцию с числом 35.35²=1225.3*4=12 и приписываем 25.Проверим этот фокус на числах 15 и 25. Вы знаете, какое число должно получиться при возведении этих чисел в квадрат.Как видите это быстро и просто. Вы сможете пользоваться этим быстрым исчислением при возведении некоторых чисел в квадрат и это вам пригодиться в работе по нашей теме. Теперь, ребята подсчитайте то количество баллов, которое вы набрали за работу в наших лабораториях и добавьте количество баллов, которое каждый из вас поставил себе за активность на уроке. Активность оценивается по пятибалльной шкале. По набранному количеству баллов вы должны поставить себе оценку за урок. Я надеюсь, что плохих оценок сегодня нет и у всех у вас хорошее настроение, такое же как у человечка на экране.Оценочные листы вместе с остальными листами, на которых отображена ваша работа в лабораториях, вы сдаете мне. Оценки ваши будут выставлены в журнал. И даже, если вы иногда допускали ошибки, это неудивительно, ведь любой человек не застрахован от ошибок, особенно, если он только учится овладевать какой-то наукой. Важно вовремя найти и исправить эти ошибки, понять, почему они появились и впредь стараться не допускать их.4.     Итоги урока.  Сегодня на уроке мы:•         Повторили определение неравенства второй степени;•         Закрепили навык использования метода интервалов при решении неравенств;•         Выработали критерии оценки своей работы, умение анализировать проделанную работу и адекватно ее оценивать.Домашнее задание: №103 (а,г)  Оценочный лист.                     Фамилия, имя­­­­­­_____________________________

Лаборатория теоретиков (максимум 5 балла)	Лаборатория исследований (максимум 4 баллов)	Лаборатория эрудитов (максимум 2 балла)	Лаборатория раскрытия тайн (максимум 5 баллов)	Активность на уроке (максимум 5 баллов)	Всего баллов	Оценка

---

Оценка «5»: 20-21 балловОценка «4»: 14-19 балловОценка «3»: ниже 14 баллов      Оценочный лист.                      Фамилия, имя­­­­­­_____________________________

Лаборатория теоретиков (максимум 5 балла)	Лаборатория исследований (максимум 4 баллов)	Лаборатория эрудитов (максимум 2 балла)	Лаборатория раскрытия тайн (максимум 5 баллов)	Активность на уроке (максимум 5 баллов)	Всего баллов	Оценка

Оценка «5»: 20-21 балловОценка «4»: 14-19 балловОценка «3»: ниже 14 баллов        Оценочный лист.                     Фамилия, имя­­­­­­_____________________________ 

Лаборатория теоретиков (максимум 5 балла)	Лаборатория исследований (максимум 4 баллов)	Лаборатория эрудитов (максимум 2 балла)	Лаборатория раскрытия тайн (максимум 5 баллов)	Активность на уроке (максимум 5 баллов)	Всего баллов	Оценка

Оценка «5»: 20-21 балловОценка «4»: 14-19 балловОценка «3»: ниже 14 баллов  «Лаборатория теоретиков».

1. 
   Какое название имеет неравенство второй степени?
   
2. 
   Как называется процесс получения корней квадратного уравнения?
   
3. 
   Как называется последовательность действий при решении неравенства?
   
4. 
   От чего зависит количество корней квадратного уравнения?
   
5. 
   Если дискриминант квадратного уравнения больше нуля, то уравнение имеет …..корня.
   
6. 
   Если дискриминант квадратного уравнения равен нулю, то уравнение имеет …..корень
   
7. 
   Как называется число в неравенстве, стоящее перед переменной?
   
8. 
        Графиком функции у= ах²+вх+с (а˃0) является ________________
   
9. 
       Графиком функции у= ах²+вх+с (а≤0) является ________________
   
10. 
    Число нулей квадратичной функции зависит от     ______________
    
11. 
          Неравенство вида (х-а)(х+в)(х-с)≤0 решается _________________
    

---

Смотрите также файлы

• Категории и возраст граждан, подлежащих профилактическим прививкам.docx

• Задача Контекст решения задачи.docx

• Прототипирование и макетирование.docx

• Вопросы для экзамена умк Школа России.docx

• Сказка для театра в 2х действиях москва 2009 действующиелица.doc