Файл: Курсовой проект по дисциплине теория конструкции локомотивов Вариант 22 Выполнил студент гр. 752 Коновалов М. А.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 159
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– прогиб пружины равный нормативному, м;
G= 8*104 МПа – модуль сдвига для стали.
Общее число витков пружины складывается из числа опорных ее витков nоп = 1.5 и числа рабочих витков части nр:
n = nоп + nр
п=1,5+9,023=10,523
4.3 Расчет на прочность резинового амортизатора
В данном разделе необходимо по результатам расчетов резинового амортизатора на прочность подобрать материал (резину) его, который по своим свойствам обеспечит допустимую деформацию амортизатора
Напряжение сжатия:
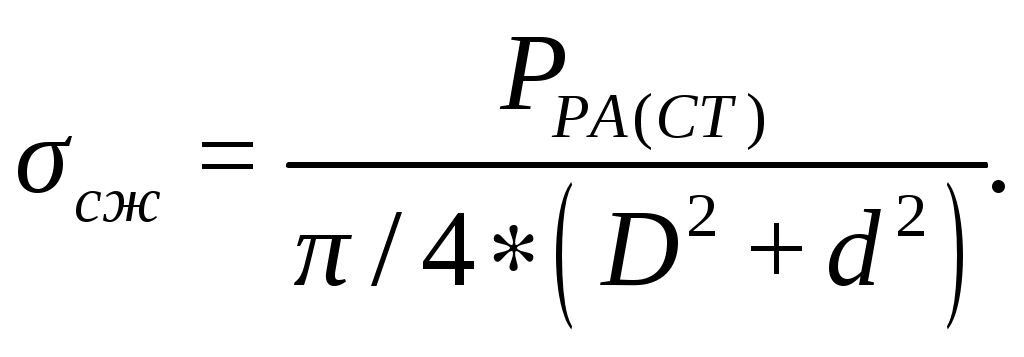 (4.15)
(4.15)
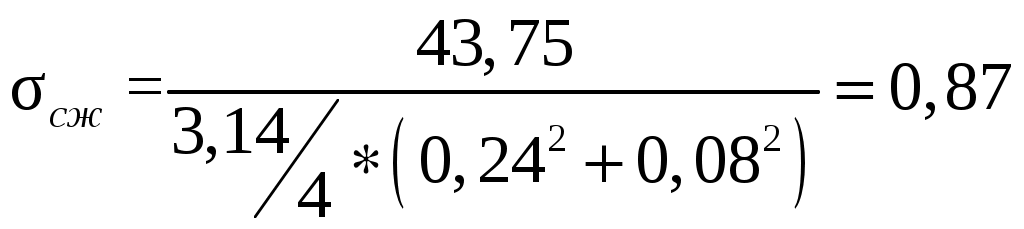 МПа
МПа
где D – наружный диаметр амортизатора, м;
d – внутренний диаметр амортизатора, м;
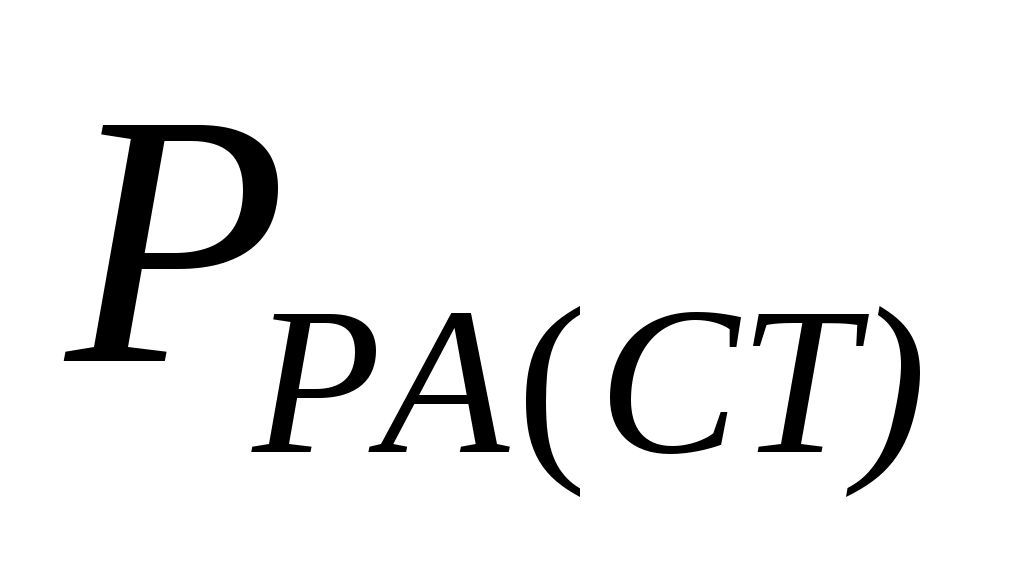 - статическая нагрузка на резиновый амортизатор
- статическая нагрузка на резиновый амортизатор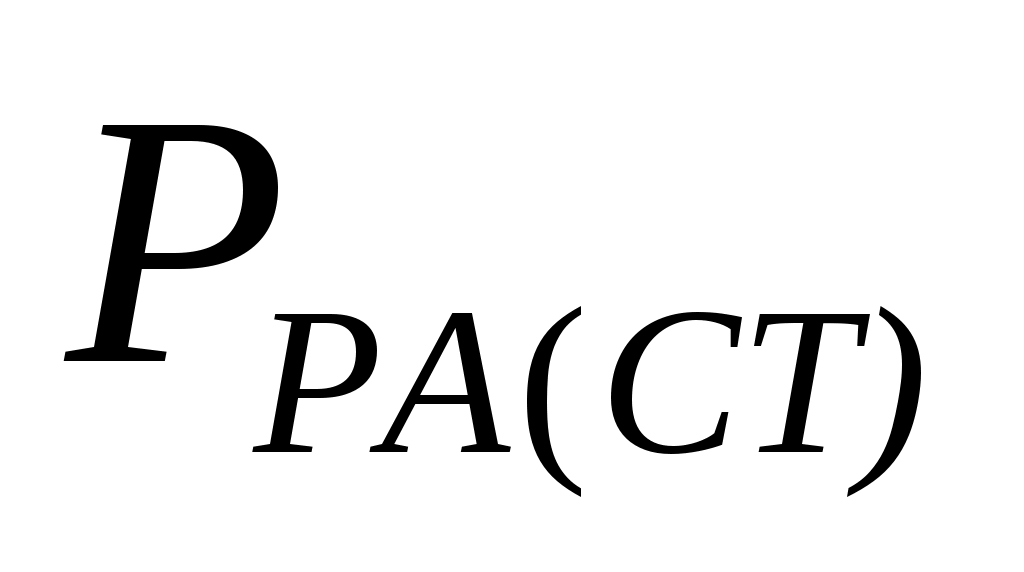 =
= 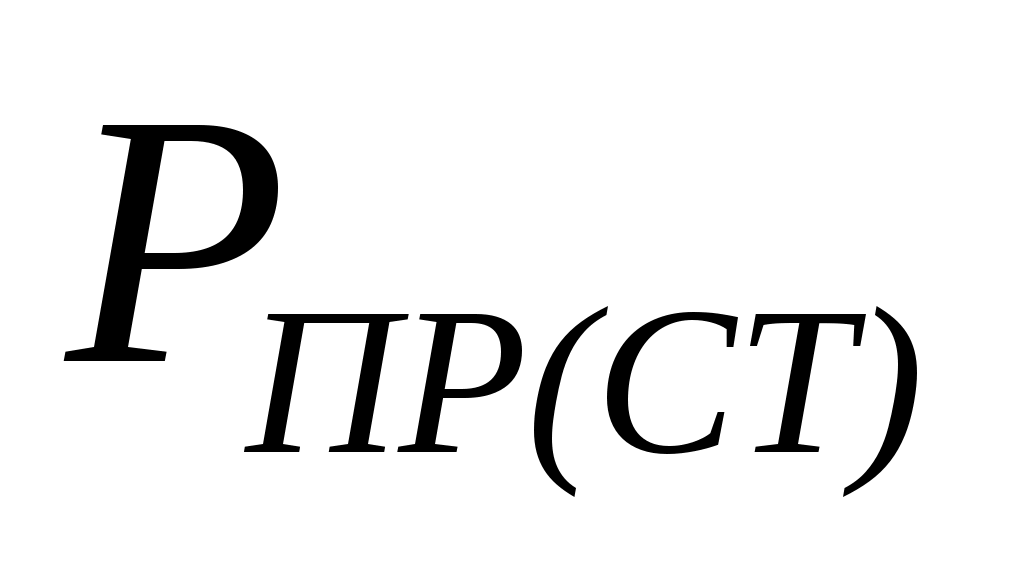 .
.
Расчётный модуль упругости находим по формуле:
Ep=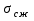 / (4.16)
/ (4.16)
Ep=0,87/0,1=8,7 МПа,
где – коэффициент деформации амортизатора, = 0,1.
Коэффициент формы, представляющий отношение площади опорной поверхности (одной) амортизатора к его полной боковой поверхности (поверхность выпучивания):
Φ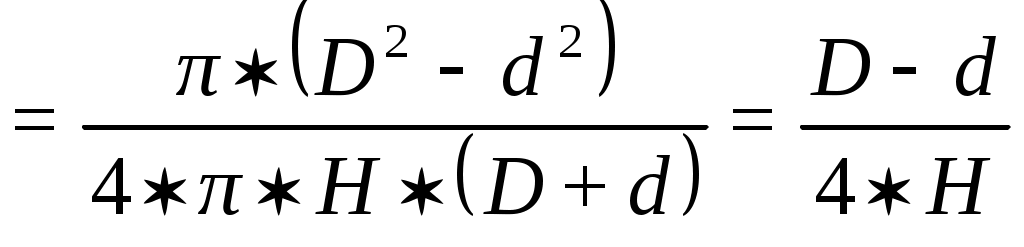 , (4.17)
, (4.17)
Φ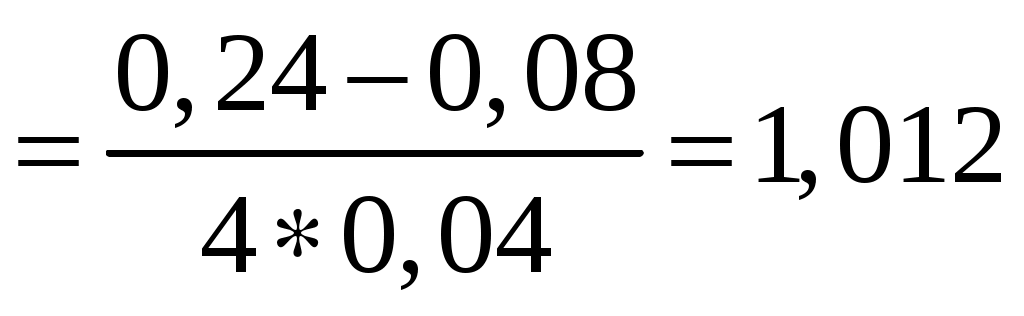
где Н – высота амортизатора, м.
Действительный модуль упругости резины определяется по формуле:
E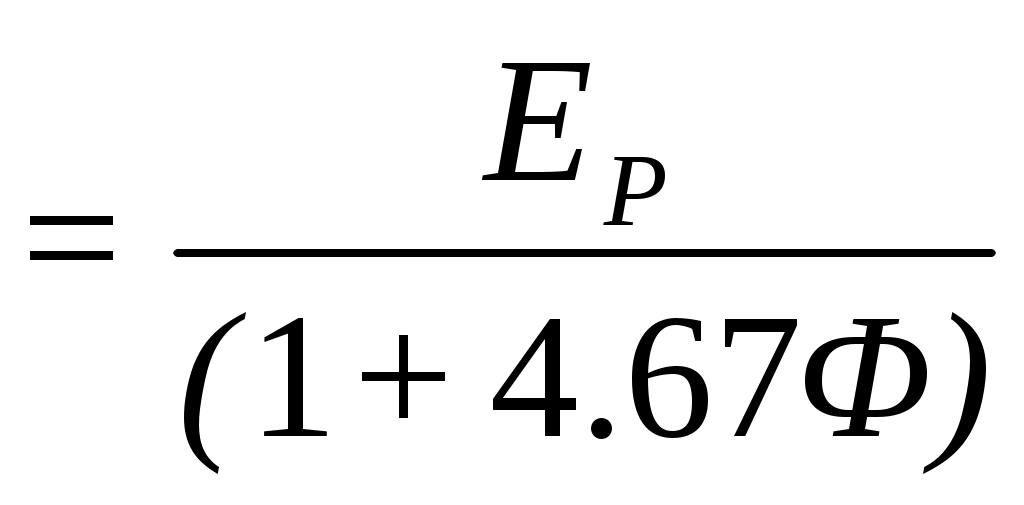
E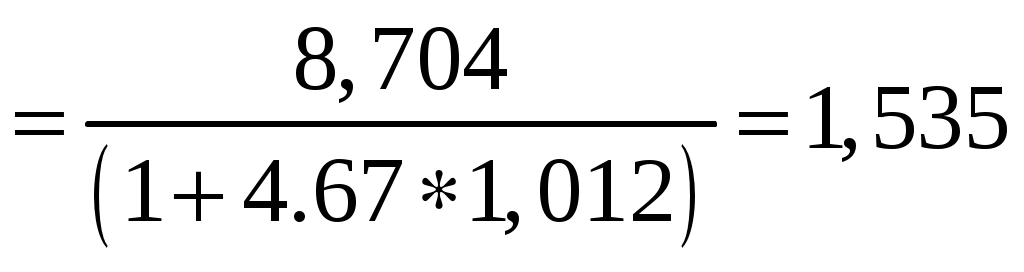 МПа
МПа
Модуль сдвига резины:
Gp =Е/3 (4.19)
Gp = 1,535/3=0,512 МПа.
Число твердости по Шору:
h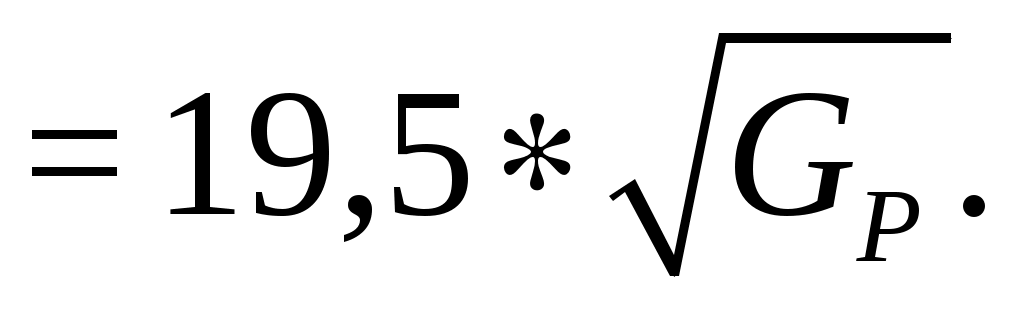 (4.20)
(4.20)
h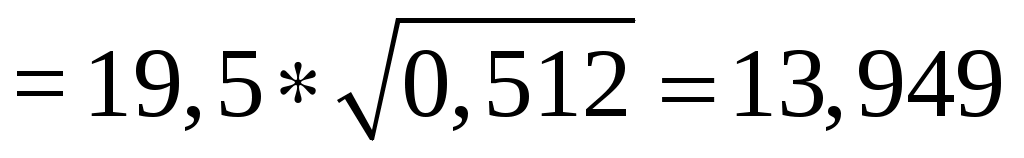
По полученной величине числа твёрдости резины и величине напряжения сжатия необходимо подобрать марку резины с описанием ее характеристик/1,2/.
Резина марки 7-1847
твердость по Шору :42.5
модуль упругости: 1.7 Мпа
модуль упругости при сдвиге: 0.48 Мпа
коэффициент Пуассона: 0.492
сопротивление разрыву: 18 Мпа
относительное удлинение при разрыве: 675%
температурный интервал работоспособности: -50 - +80
Статический прогиб резинового амортизатора из условия его долговечности определится из выражения:
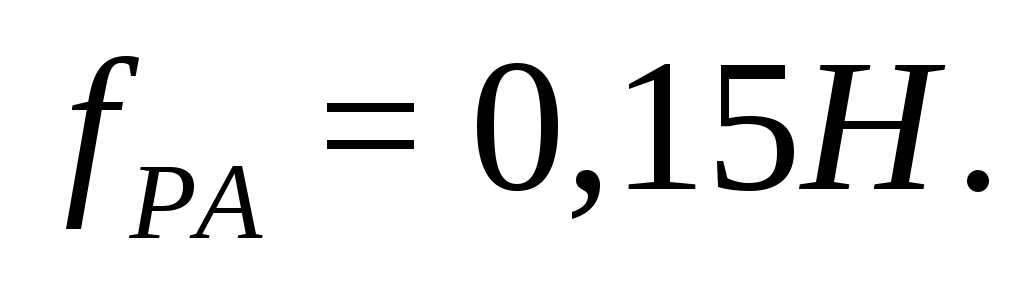 (4.21)
(4.21)
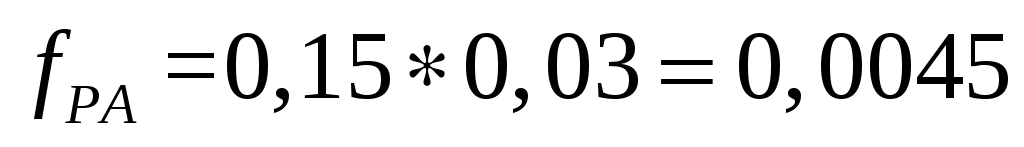 м
м
где Н – высота амортизатора, м.
4.4 Определение статического прогиба рессорного подвешивания
Статический прогиб показывает величину осадки упругих элементов под действием статической нагрузки. В зависимости от схемы нагружения рессорного подвешивания, его статический прогиб определяется с учетом статических прогибов упругих элементов.
Рессорное подвешивание, как известно, разделяется по ступеням: первая ступень (букса колесной пары – рама тележки) и вторая ступень (рама тележки - кузов). Общий статический прогиб рессорного подвешивания складывается из прогибов данных ступеней:
fст= fст1

fn1=(4.91+4*0.136)/(36*4.91+0.136)=0.028
5.Геометрическое вписывание тепловоза в кривые
Для того чтобы обеспечивать движение локомотива по кривому участку пути, приходится учитывать особенности такого движения как при укладке пути, так и при конструировании локомотивного экипажа. При большой жёсткой базе локомотива может произойти заклинивание гребней бандажей внутри рельсовой колеи кривых малого радиуса. Для того чтобы этого не произошло кривые малого радиуса укладывают с увеличенной шириной колеи.
Для облегчения вписывания локомотивного экипажа в кривые малого радиуса применяют поворотные тележки и делают осевые разбеги колёсных пар.
Для оценки целесообразности применения мероприятий, обеспечивающих прохождение локомотива по кривым, необходимо прежде всего рассмотреть геометрические соотношения между размерами рельсовой колеи и локомотивного экипажа. Решение этих вопросов составляет предмет расчётов, называемых геометрическим вписыванием в кривые.
Из-за различия в размерах кривой, базы экипажа и зазора в кривой, применение обычного масштаба для решения задач геометрического вписывания графическим способом невозможно. Чтобы использовать графический метод вписывания, приходится прибегать к специальным приёмам.
Если для поперечных и продольных направлений выбрать различные, не связанные друг с другом масштабы, то окружность, изображающая круговую кривую рельсовой колеи, преобразуется в эллипс, который на участке, где вписывается локомотив (у вершины эллипса), с большой степенью точности может быть заменен параболой. Этот способ вписывания называется параболическим.
Порядок вписывания.
1. Вычерчивается база локомотива в масштабе mx=1:n, причём можно принять п равным 25÷50.
2. Находят ординаты рельсовых путей. Ординаты наружного рельса определяют по формуле:
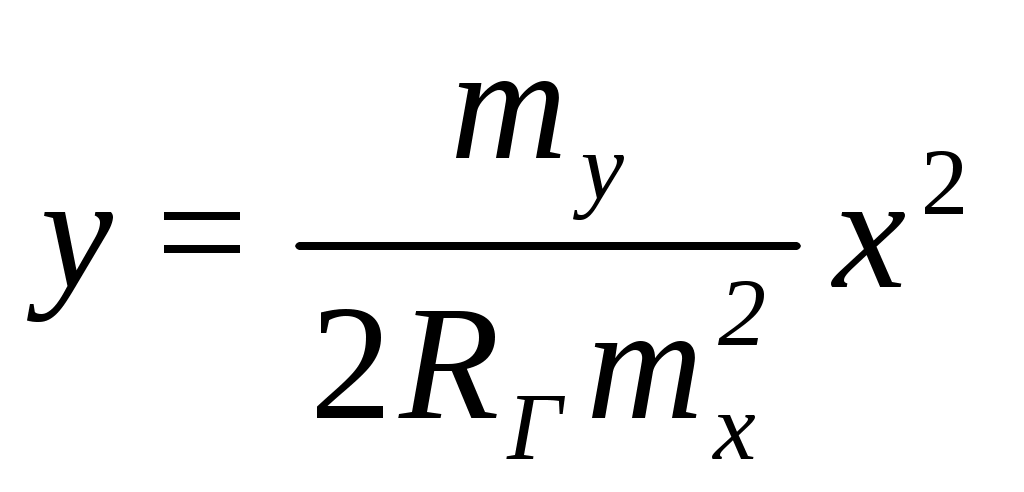 , (5.1)
, (5.1)
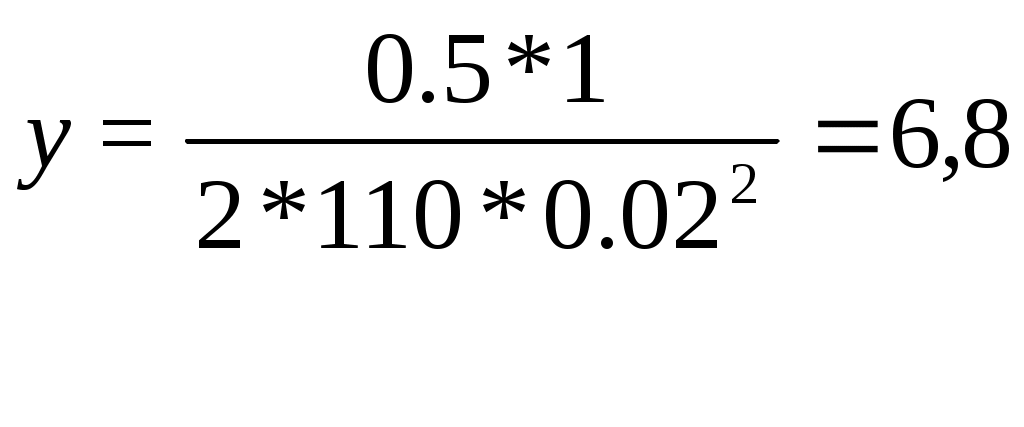
где х - текущие абсциссы базы локомотива (чертежные), заданный радиус кривой, мм;
RГ – заданный радиус кривой, мм;
my- масштаб по вертикали, который обычно принимают равным 1:1 или 1:2.
Для более точного построения параболы необходимо брать больше значений х. Расчёт координат точек параболы свести в табл. 7.
По вычисленным значениям y строят параболу, изображающую наружный рельс (рис.2.).
Изображение внутреннего рельса будет получено, если параболу наружного рельса сдвинуть параллельно самой себе вдоль оси y на величину
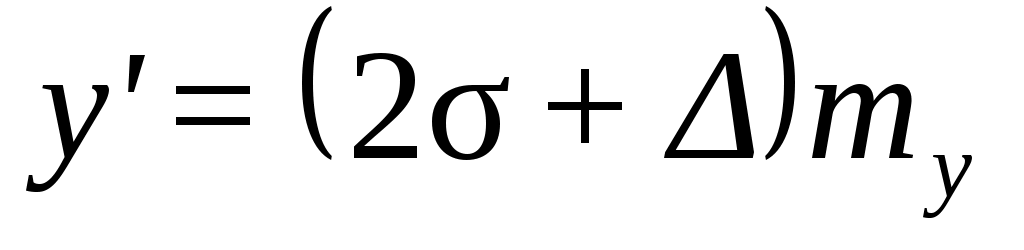 (5.2)
(5.2)
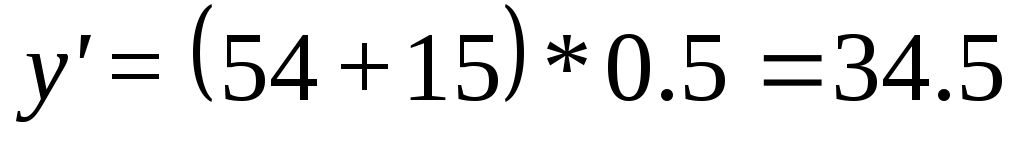
где, 2+ – величина зазора колесной пары и колеи, мм.
Величину зазоров 2 + следует принимать минимальную с учетом допускаемых отклонений от номинальных размеров. Согласно ПТЭ на прямых участках пути и на кривых радиусом 350 м и более:
2 =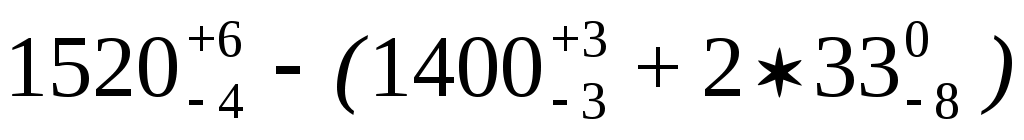 мм - при скорости до 120 км/ч;
мм - при скорости до 120 км/ч;
2 =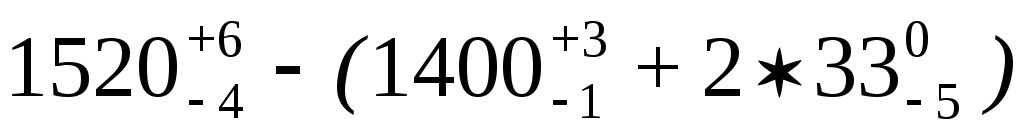 мм - при скорости от 121 до 140 км/ч.
мм - при скорости от 121 до 140 км/ч.
Согласно ПТЭ:
= 10 мм – при радиусе кривой от 349 до 300 м;
= 15 мм – при радиусе кривой от 299 м и менее.
Схема экипажа размещается в масштабе mx так, чтобы продольная ось кузова была параллельна оси ох
При данных mX и mY стрела в вертикальном направлении получается в натуральную величину.
При параболическом методе все зазоры и отклонения должны измеряться только вертикально. Углы βП, град получаются в искаженном виде и определяются, с учетом замеренных на диаграмме углов
βЧЕР, град из выражения:
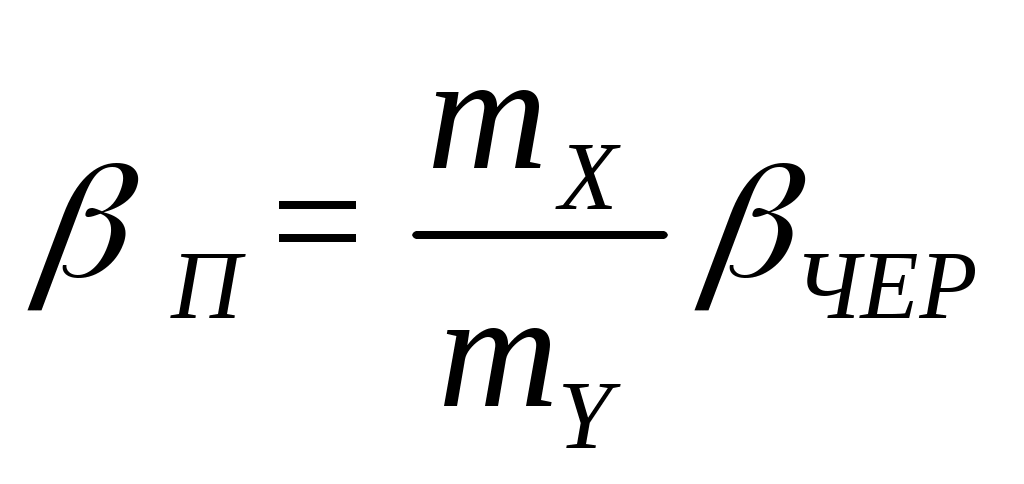 (5.2)
(5.2)
1) Отброс к наружному рельсу:
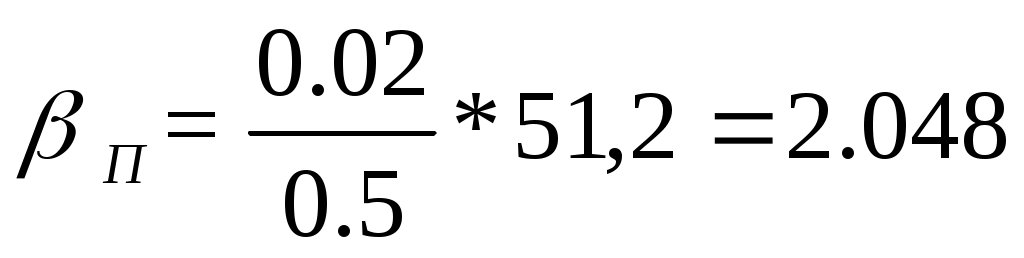
2) Отброс к внутреннему рельсу:
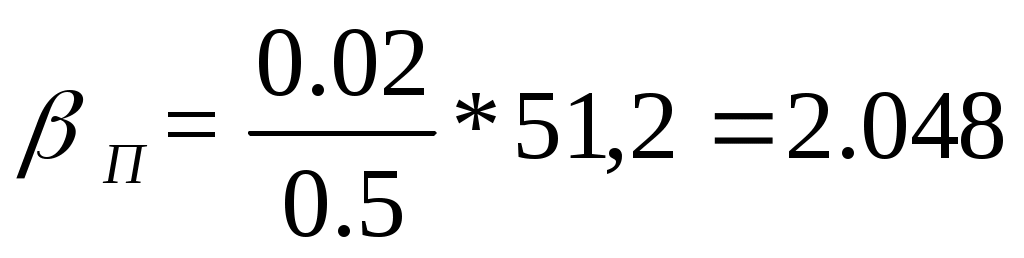
3) Наибольший перекос:
a)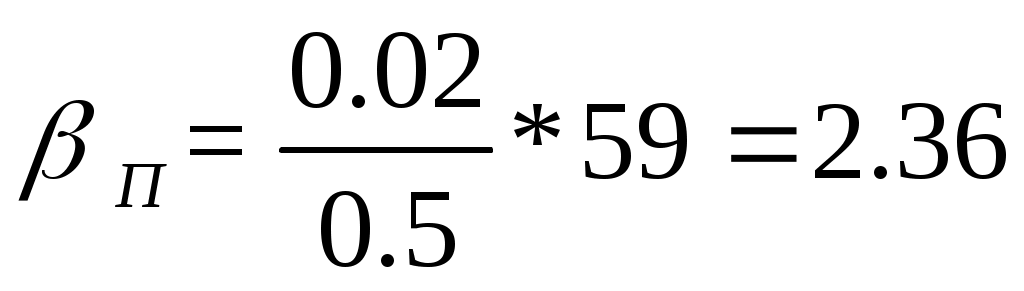
б)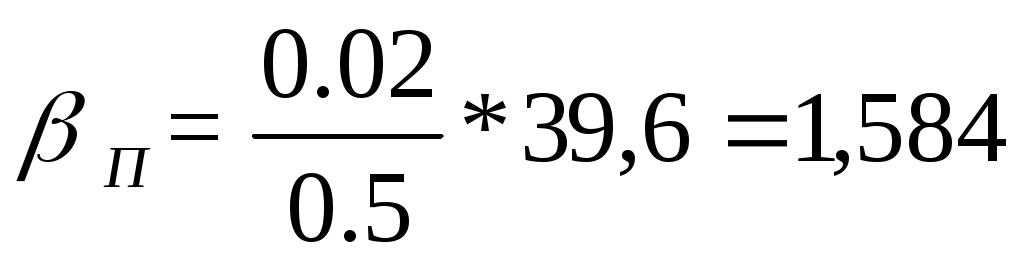
При геометрическом вписывании исследуются следующие положения экипажа:
1) положение отброса к наружному рельсу (установка по хорде),
2) положение перекоса;
3) отброс к внутреннему рельсу.
При всех исследованных положениях определяются:
а) величины зазоров между гребнем бандажа и рельсом средних колесных пар;
б) величины осевых разбегов средних колесных пар;
в) углы между осями кузова и тележек.
6. Динамическое вписывание проектируемого тепловоза в кривую
6.1 Общие сведения
Решение задач динамического вписывания предусматривает определение максимальной скорости движения локомотива в кривой, при которой обеспечивается безопасность движения и комфортабельность для обслуживающего персонала и пассажиров. Безопасность движения подвижного состава оценивается критериями безопасности, которые характеризуют величины боковых давле6ний на рельсы и упругое отжатие рельсов под действием этих усилий. Чрезмерная величина бокового давления может привести к набеганию колеса на рельс и сходу локомотива с рельсов.
Критерием комфортабельности является величина непогашенного ускорения н . Его величина не может превышать 0,7 м/с2. Это – максимальное ускорение, при котором человек не испытывает вредного воздействия низкочастотных колебаний экипажной части подвижного состава при входе экипажа в кривую.
При динамическом вписывании определяются горизонтальные усилия, передаваемые колесами локомотивного экипажа (тележки) на головки рельсов для наихудшего сочетания действующих нагрузок – положения наибольшего перекоса – положение при котором передняя колесная пара тележки прижата к наружнему рельсу, а задняя – к внутреннему. На движущийся локомотив в кривой действует множество сил, весь комплекс которых учесть не всегда удается. Поэтому задачи динамического вписывания выполняют с некоторыми допущениями, так как учитываются только следующие силы:
G= 8*104 МПа – модуль сдвига для стали.
Общее число витков пружины складывается из числа опорных ее витков nоп = 1.5 и числа рабочих витков части nр:
n = nоп + nр
п=1,5+9,023=10,523
4.3 Расчет на прочность резинового амортизатора
В данном разделе необходимо по результатам расчетов резинового амортизатора на прочность подобрать материал (резину) его, который по своим свойствам обеспечит допустимую деформацию амортизатора
Напряжение сжатия:
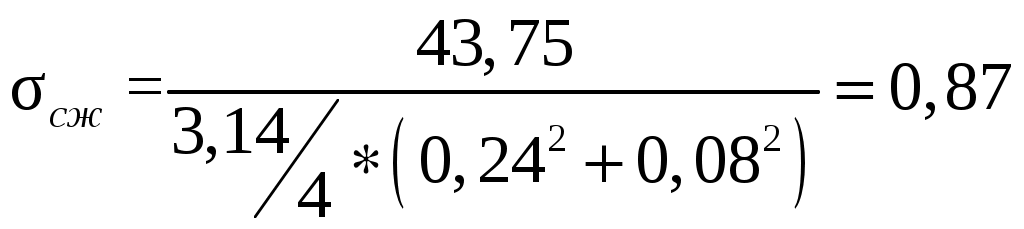 МПа
МПагде D – наружный диаметр амортизатора, м;
d – внутренний диаметр амортизатора, м;
Расчётный модуль упругости находим по формуле:
Ep=
Ep=0,87/0,1=8,7 МПа,
где – коэффициент деформации амортизатора, = 0,1.
Коэффициент формы, представляющий отношение площади опорной поверхности (одной) амортизатора к его полной боковой поверхности (поверхность выпучивания):
Φ
Φ
где Н – высота амортизатора, м.
Действительный модуль упругости резины определяется по формуле:
E
E
Модуль сдвига резины:
Gp =Е/3 (4.19)
Gp = 1,535/3=0,512 МПа.
Число твердости по Шору:
h
h
По полученной величине числа твёрдости резины и величине напряжения сжатия необходимо подобрать марку резины с описанием ее характеристик/1,2/.
Резина марки 7-1847
твердость по Шору :42.5
модуль упругости: 1.7 Мпа
модуль упругости при сдвиге: 0.48 Мпа
коэффициент Пуассона: 0.492
сопротивление разрыву: 18 Мпа
относительное удлинение при разрыве: 675%
температурный интервал работоспособности: -50 - +80
Статический прогиб резинового амортизатора из условия его долговечности определится из выражения:
где Н – высота амортизатора, м.
4.4 Определение статического прогиба рессорного подвешивания
Статический прогиб показывает величину осадки упругих элементов под действием статической нагрузки. В зависимости от схемы нагружения рессорного подвешивания, его статический прогиб определяется с учетом статических прогибов упругих элементов.
Рессорное подвешивание, как известно, разделяется по ступеням: первая ступень (букса колесной пары – рама тележки) и вторая ступень (рама тележки - кузов). Общий статический прогиб рессорного подвешивания складывается из прогибов данных ступеней:
fст= fст1
fn1=(4.91+4*0.136)/(36*4.91+0.136)=0.028
5.Геометрическое вписывание тепловоза в кривые
Для того чтобы обеспечивать движение локомотива по кривому участку пути, приходится учитывать особенности такого движения как при укладке пути, так и при конструировании локомотивного экипажа. При большой жёсткой базе локомотива может произойти заклинивание гребней бандажей внутри рельсовой колеи кривых малого радиуса. Для того чтобы этого не произошло кривые малого радиуса укладывают с увеличенной шириной колеи.
Для облегчения вписывания локомотивного экипажа в кривые малого радиуса применяют поворотные тележки и делают осевые разбеги колёсных пар.
Для оценки целесообразности применения мероприятий, обеспечивающих прохождение локомотива по кривым, необходимо прежде всего рассмотреть геометрические соотношения между размерами рельсовой колеи и локомотивного экипажа. Решение этих вопросов составляет предмет расчётов, называемых геометрическим вписыванием в кривые.
Из-за различия в размерах кривой, базы экипажа и зазора в кривой, применение обычного масштаба для решения задач геометрического вписывания графическим способом невозможно. Чтобы использовать графический метод вписывания, приходится прибегать к специальным приёмам.
Если для поперечных и продольных направлений выбрать различные, не связанные друг с другом масштабы, то окружность, изображающая круговую кривую рельсовой колеи, преобразуется в эллипс, который на участке, где вписывается локомотив (у вершины эллипса), с большой степенью точности может быть заменен параболой. Этот способ вписывания называется параболическим.
Порядок вписывания.
1. Вычерчивается база локомотива в масштабе mx=1:n, причём можно принять п равным 25÷50.
2. Находят ординаты рельсовых путей. Ординаты наружного рельса определяют по формуле:
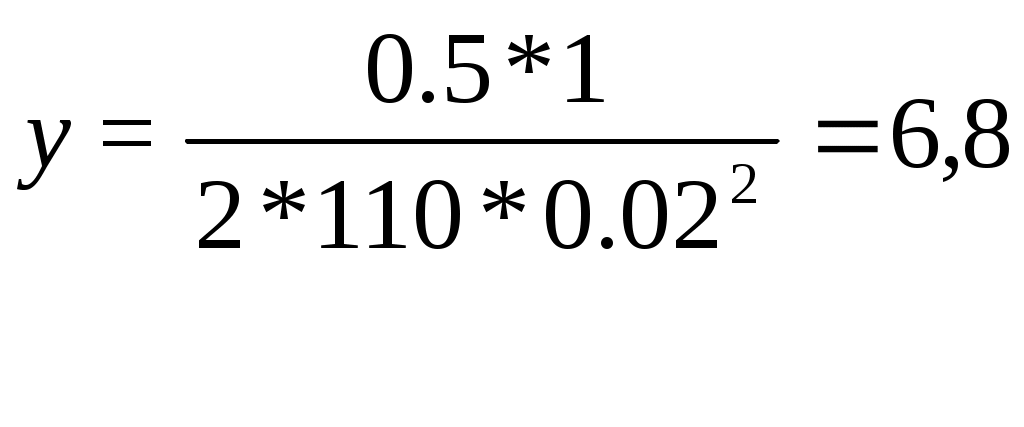
где х - текущие абсциссы базы локомотива (чертежные), заданный радиус кривой, мм;
RГ – заданный радиус кривой, мм;
my- масштаб по вертикали, который обычно принимают равным 1:1 или 1:2.
Для более точного построения параболы необходимо брать больше значений х. Расчёт координат точек параболы свести в табл. 7.
Таблица 3
| X | -110 | -90 | -70 | -50 | -30 | -10 | 10 | 30 | 50 | 70 | 90 | 110 |
| X2 | 1.21 | 0.8 | 0.49 | 0.25 | 0.09 | 0.01 | 0.01 | 0.09 | 0.25 | 0.49 | 0.8 | 1.21 |
| Y | 6.9 | 4.6 | 2.7 | 1.42 | 0.51 | 0.057 | 0.057 | 0.51 | 1.42 | 2.7 | 4.6 | 6.9 |
По вычисленным значениям y строят параболу, изображающую наружный рельс (рис.2.).
Изображение внутреннего рельса будет получено, если параболу наружного рельса сдвинуть параллельно самой себе вдоль оси y на величину
где, 2+ – величина зазора колесной пары и колеи, мм.
Величину зазоров 2 + следует принимать минимальную с учетом допускаемых отклонений от номинальных размеров. Согласно ПТЭ на прямых участках пути и на кривых радиусом 350 м и более:
2 =
2 =
Согласно ПТЭ:
= 10 мм – при радиусе кривой от 349 до 300 м;
= 15 мм – при радиусе кривой от 299 м и менее.
Схема экипажа размещается в масштабе mx так, чтобы продольная ось кузова была параллельна оси ох
При данных mX и mY стрела в вертикальном направлении получается в натуральную величину.
При параболическом методе все зазоры и отклонения должны измеряться только вертикально. Углы βП, град получаются в искаженном виде и определяются, с учетом замеренных на диаграмме углов
βЧЕР, град из выражения:
1) Отброс к наружному рельсу:
2) Отброс к внутреннему рельсу:
3) Наибольший перекос:
a)
б)
При геометрическом вписывании исследуются следующие положения экипажа:
1) положение отброса к наружному рельсу (установка по хорде),
2) положение перекоса;
3) отброс к внутреннему рельсу.
При всех исследованных положениях определяются:
а) величины зазоров между гребнем бандажа и рельсом средних колесных пар;
б) величины осевых разбегов средних колесных пар;
в) углы между осями кузова и тележек.
6. Динамическое вписывание проектируемого тепловоза в кривую
6.1 Общие сведения
Решение задач динамического вписывания предусматривает определение максимальной скорости движения локомотива в кривой, при которой обеспечивается безопасность движения и комфортабельность для обслуживающего персонала и пассажиров. Безопасность движения подвижного состава оценивается критериями безопасности, которые характеризуют величины боковых давле6ний на рельсы и упругое отжатие рельсов под действием этих усилий. Чрезмерная величина бокового давления может привести к набеганию колеса на рельс и сходу локомотива с рельсов.
Критерием комфортабельности является величина непогашенного ускорения н . Его величина не может превышать 0,7 м/с2. Это – максимальное ускорение, при котором человек не испытывает вредного воздействия низкочастотных колебаний экипажной части подвижного состава при входе экипажа в кривую.
При динамическом вписывании определяются горизонтальные усилия, передаваемые колесами локомотивного экипажа (тележки) на головки рельсов для наихудшего сочетания действующих нагрузок – положения наибольшего перекоса – положение при котором передняя колесная пара тележки прижата к наружнему рельсу, а задняя – к внутреннему. На движущийся локомотив в кривой действует множество сил, весь комплекс которых учесть не всегда удается. Поэтому задачи динамического вписывания выполняют с некоторыми допущениями, так как учитываются только следующие силы: